[Title link] http://codeforces.com/problemset/problem/734/F

[title]

Give you two arrays b and c.
Then let you find a non-negative array a to satisfy the relationship given in the question.

[Abstract]

Have a conclusion.
(x and y + x or y)=x+y
Then add up all the n formulas.
Let d[i]=b[i]+c[i] * 1;
be
d[i]=n∗a[i]+∑a⋅⋅⋅②
Add up all the formulas.
∑d=2∗n∑a⋅⋅⋅③
It can be obtained by formula 3.
∑a=∑d/(2∗n)
Re-substitution
a[i]=(d[i]−∑d/(2∗n))/n
Namely
a[i]=(2∗n∗d[i]−∑d)/(2∗n2)
For cases where a[i] < 0 or a[i] is not an integer.
Return to no solution.
But that's not enough.
It's still possible to misunderstand.
Also verify whether the obtained a[i] can get b[i] and c[i] according to that rule;
But the complexity of O(N2) can be calculated directly.
One by one is faster here.
We calculate the number kj of all aj at pos i tion 1.
Then there is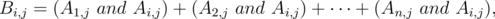


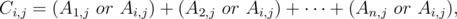
Here we can quickly get Bi,j and Ci,j through Ai,j and kj.
Namely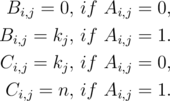

Then according to the obtained Ci,j and Bi,j;
Multiply the x power of the corresponding 2 according to the bit weight.
Then add it up.
See if the c and b arrays are the same as the given c and b arrays.

[Number Of WA]

0

[Complete code]

#include <bits/stdc++.h>
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define ms(x,y) memset(x,y,sizeof x)
#define Open() freopen("F:\\rush.txt","r",stdin)
#define Close() ios::sync_with_stdio(0),cin.tie(0)

typedef pair<int,int> pii;
typedef pair<LL,LL> pll;

const int dx[9] = {0,1,-1,0,0,-1,-1,1,1};
const int dy[9] = {0,0,0,-1,1,-1,1,-1,1};
const double pi = acos(-1.0);
const int N = 2e5+100;

int n;
LL b[N],c[N],d[N],sumd = 0,a[N],ans[N];
int B[N][65],C[N][65];
LL bin[65];

void out()
{
    cout << -1 << endl;
    exit(0);
}

int main()
{
    //Open();
    Close();//scanf,puts,printf not use
    bin[0] = 1;
    rep1(i,1,62)
        bin[i] = bin[i-1]<<1;
    cin >> n;
    rep1(i,1,n)
        cin >> b[i];
    rep1(i,1,n)
    {
        cin >> c[i];
        d[i] = b[i]+c[i];
        sumd += d[i];
    }
    rep1(i,1,n)
    {
        a[i] = 1LL*2*n*d[i]-sumd;
        LL temp = 1LL*2*n*n;
        if (a[i]%temp!=0)  out();
        a[i]/=temp;
        if (a[i]<0) out();
        ans[i] = a[i];
    }
    LL ma = *max_element(a+1,a+1+n);
    int limit = 0;
    while (ma)
    {
        ma>>=1;
        limit++;
    }
    rep1(i,0,limit-1)
    {
        int k = 0;
        rep1(j,1,n)
            if (a[j]&bin[i])
                k++;
        rep1(j,1,n)
        {
            if (a[j]&bin[i])
            {
                B[j][i]+=k,C[j][i]+=n;
            }
            else
                //a[j]%1==0
                C[j][i]+=k;
        }
    }
    rep1(i,1,n)
    {
        LL tb = 0;
        rep1(j,0,limit-1)
            tb = tb+B[i][j]*bin[j];
        LL tc = 0;
        rep1(j,0,limit-1)
            tc = tc+C[i][j]*bin[j];
        if (tb!=b[i]||tc!=c[i])
            out();
    }
    rep1(i,1,n)
        cout << ans[i] <<' ';
    //init??????
    return 0;
}