Title Link: Click to view

Main idea: first of all, give n heap stones and a k value. They operate according to the rules in turn. The one who can't operate is the failure. Each time, there are two operations:

1. Take a stone from any pile
2. Choose a pile of even stones, and convert them into a pile of k x/2 stones.

Both will follow the best solution and ask who can win the game

Problem analysis: we can think of n-heap stones as an independent game, so the problem is converted into finding the sg function of each pile of stones and then judging the XOR. But there are two problems. First, the problem is not the normal sg table, and then the number of each pile of stones reaches 1e9, which is not realistic.

We can first play a watch to see the first few rules, read most of the blog on the Internet did not teach how to play a watch to find the rules, yesterday I asked my teammates, it's really quite simple, but I won't. Now it's a meeting

First of all, it is easy to see that if the sg function mainly depends on the parity of k, if k is an odd number, then all but one pile can cancel each other. If k is an even number, then all the newly generated piles can cancel each other. With this conclusion, we can get the general framework of sg function:

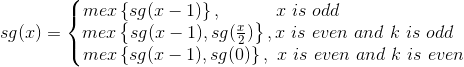
sg function:

const int N=100;//How many times does it reach

int sg[N];

bool mex[10];

void get_sg() 
{
	sg[0]=0;
	for(int i=1;i<N;i++)
	{
		memset(mex,false,sizeof(mex));
		if(i&1)
			mex[sg[i-1]]=true;
		else
		{
			if(k&1)
			{
				mex[sg[i-1]]=true;
				mex[sg[i/2]]=true;
			}
			else
			{
				mex[sg[i-1]]=true;
				mex[sg[0]]=true;
			}
		}
		for(int j=0;j<10;j++)
			if(!mex[j])
			{
				sg[i]=j;
				break;
			}
	}
}

Then we can find the law. We can easily see that when x is a large odd number (odd number greater than 3), the values of sg functions are all 0, that is, they are required to fail. When we deal with even numbers, we only need to pay attention to the values of sg functions divided by 2, because if they can directly reach the odd state, then their sg values must be 1, and they can be returned directly.

When x is even, we should judge it according to the odd and even of K. at first, I thought that the value of sg function is related to the power of 2 in X, but later I found that it is not so right. I found it after observing (searching for solutions on the Internet), because when k is even, it has no effect on the result, so the sg value of X is all 1. When k is odd, we should judge the sg value of x/2, and we can recurse forward according to the previous The value pushes the current value. The logic is as follows:

1. sg value of current item is 0, and sg value of subsequent item is 1 (definition of mex function)
2. The sg value of the current item is 1, and that of the subsequent items is 2 (because sg(x)=mex{sg(x-1),sg(x/2)}).
3. sg value of current item is 2, and sg value of subsequent item is 1 (definition of mex function)

This logic is well understood in combination with the logic of sg function mentioned above. If it is really not possible, or the technology of finding laws is really powerful, then we can directly find out the laws.

Implementation code:

#include<iostream>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<climits>
#include<cmath>
#include<cctype>
#include<stack>
#include<queue>
#include<list>
#include<vector>
#include<set>
#include<map>
#include<sstream>
#include<unordered_map>
using namespace std;
 
typedef long long LL;
 
const int inf=0x3f3f3f3f;
 
const int N=1e3+100;

int k;
/*
When k is even:
0:0
1:1
2:2
 From 3:
Odd number: 0
 Even number: 1

When k is odd:
0:0
1:1
2:0
3:1
4:2
 Odd number: 0
 Even number: related to sg of x/2:
	x/2=2 Or x/2=0:1
	x/2=1: 2 
*/
int get_sg(int x)
{
	if(k&1)
	{
		if(x<5)
		{
			if(x==0)
				return 0;
			else if(x==1)
				return 1;
			else if(x==2)
				return 0;
			else if(x==3)
				return 1;
			else if(x==4)
				return 2;
		}
		else
		{
			if(x&1)
				return 0;
			else
				return get_sg(x/2)==1?2:1; 
		}
	}
	else
	{
		if(x<=2)
			return x;
		else
			return (x&1)^1; 
	}
}

int main()
{
//  freopen("input.txt","r",stdin);
	int n;
	scanf("%d%d",&n,&k);
	int ans=0;
	while(n--)
	{
		int num;
		scanf("%d",&num);
		ans^=get_sg(num);
	} 
	if(ans)
		printf("Kevin\n");
	else
		printf("Nicky\n");
	
	
	
	
	
   	
   	
   	
     
     
     
     
     
     
     
    return 0;
}