=== ===

Put here Portal

=== ===

Title Solution

This problem means giving an undirected graph the minimum point weight of all points that can be reached from a point to a point without repeating points. It also supports modifying the point weight of a point.
Because the point of arrival can't be repeated, when it is at a certain point, all the points that belong to the same point double-connected component can be used to count the answers. Since the point double-shrinkage point is a tree after it, if we can set the point weight of each point double-shrinkage point to the minimum of all points in it, then we can run the chain directly.
However, it is a very troublesome job to extract the dot pairs, then number them and count the dot weights. Because the cut points belong to the dual-connected components of multiple points at the same time, there will be many details to implement.

A better way to write is to create a new point for each point, and then connect each point to the point it belongs to by one side. In this way, all cut points will be connected to several points, instead of cutting points will only be connected to one point. In this case, the figure in the sample is like this: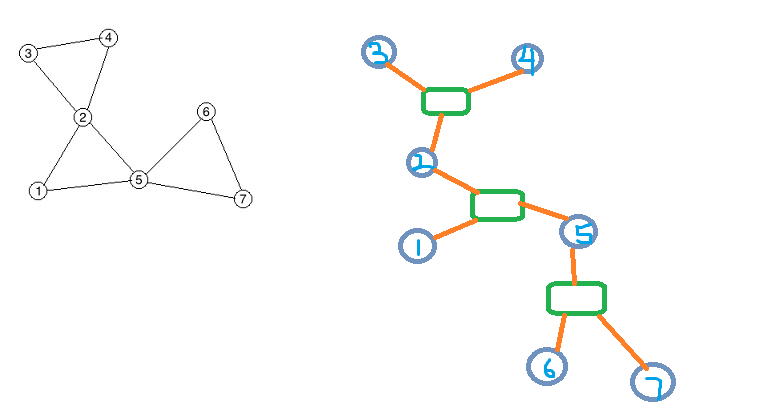

It can be seen that the pattern of trees must be one point after another and then one point after another. So the father of each point must be a block representing the point pair, and this point must belong to the point pair. Then use a multiset to maintain the minimum inside the point pair and update all points to its parent node.
The query can be directly linked, but there is a problem that if the LCA of two points is a block, then the father of this block should also be a cut point belonging to this block, and this point should be judged specially.
In addition to modifying the current point, it needs to be maintained in the multiset.

Code

#include<set>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,q,val[100010],cnt,tot,p[100010],a[200010],nxt[200010],w[200010],low[200010];
int top,st[200010],rec,point,father[200010];
bool mak[200010];
multiset<int> s[100010];
void add(int x,int y){
    tot++;a[tot]=y;nxt[tot]=p[x];p[x]=tot;
}
int rev(int i){return (i&1)?(i+1):(i-1);}
int find(int x){
    if (father[x]==x) return father[x];
    father[x]=find(father[x]);
    return father[x];
}
void merge(int x,int y){
    int r1,r2;
    r1=find(x);r2=find(y);
    if (r1!=r2) father[r1]=r2;
}
namespace Tree{
    int p[200010],a[400010],nxt[400010],top[200010],size[200010],son[200010],fa[200010];
    int w[200010],cnt,tot,num[200010],Min[800010],deep[200010],val[200010],N;
    multiset<int>::iterator it;
    void add(int x,int y){
        tot++;a[tot]=y;nxt[tot]=p[x];p[x]=tot;
    }
    void dfs(int u){
        deep[u]=deep[fa[u]]+1;
        size[u]=1;son[u]=0;
        for (int i=p[u];i!=0;i=nxt[i])
          if (a[i]!=fa[u]){
              fa[a[i]]=u;dfs(a[i]);
              size[u]+=size[a[i]];
              if (size[a[i]]>size[son[u]])
                son[u]=a[i];
          }
    }
    void dfs_again(int u,int tp){
        top[u]=tp;w[u]=++cnt;num[cnt]=u;
        if (son[u]!=0) dfs_again(son[u],tp);
        for (int i=p[u];i!=0;i=nxt[i])
          if (a[i]!=fa[u]&&a[i]!=son[u])
            dfs_again(a[i],a[i]);
    }
    void update(int i){Min[i]=min(Min[i<<1],Min[(i<<1)+1]);}
    void build(int i,int l,int r){
        if (l==r){Min[i]=val[num[l]];return;}
        int mid=(l+r)>>1;
        build(i<<1,l,mid);
        build((i<<1)+1,mid+1,r);
        update(i);
    }
    void BuildTree(int point){
        N=point;
        dfs(1);dfs_again(1,1);
        for (int i=1;i<=n;i++)
          if (fa[i]>n)//Add the value of the current point to its father
            s[fa[i]-n].insert(val[i]);
        for (int i=n+1;i<=N;i++){
            it=s[i-n].begin();//Find the smallest element in the set
            val[i]=(*it);
        }
        build(1,1,N);
    }
    int ask(int i,int l,int r,int left,int right){
        if (left<=l&&right>=r) return Min[i];
        int mid=(l+r)>>1,ans=0x7fffffff;
        if (left<=mid) ans=min(ans,ask(i<<1,l,mid,left,right));
        if (right>mid) ans=min(ans,ask((i<<1)+1,mid+1,r,left,right));
        return ans;
    }
    void change(int i,int l,int r,int x,int v){
        if (l==r){Min[i]=v;return;}
        int mid=(l+r)>>1;
        if (x<=mid) change(i<<1,l,mid,x,v);
        else change((i<<1)+1,mid+1,r,x,v);
        update(i);
    }
    int Query(int x,int y){
        int ans=0x7fffffff;
        while (top[x]!=top[y]){
            if (deep[top[x]]<deep[top[y]]) swap(x,y);
            ans=min(ans,ask(1,1,N,w[top[x]],w[x]));
            x=fa[top[x]];
        }
        if (deep[x]>deep[y]) swap(x,y);
        ans=min(ans,ask(1,1,N,w[x],w[y]));
        if (x>n) ans=min(ans,val[fa[x]]);
        return ans;
    }
    void Change(int x,int y){
        int pos=fa[x]-n;
        if (pos>0){//Note that only when there's a little bit more to change.
            it=s[pos].find(val[x]);
            s[pos].erase(it);//Delete the value of the iterator position
            s[pos].insert(y);
            it=s[pos].begin();
            val[fa[x]]=(*it);
            change(1,1,N,w[fa[x]],val[fa[x]]);
        }
        change(1,1,N,w[x],y);val[x]=y;
    }
    void print(int N){
        for (int i=1;i<=N;i++)
          for (int j=p[i];j!=0;j=nxt[j])
            printf("%d %d\n",i,a[j]);
    }
}
void Tarjan(int u,int fa,int rt){
    w[u]=low[u]=++cnt;st[++top]=u;
    for (int i=p[u];i!=0;i=nxt[i])
      if (w[a[i]]==0){
          if (u==1) ++rec;
          Tarjan(a[i],u,rt);
          low[u]=min(low[u],low[a[i]]);
          if (low[a[i]]>=w[u]){
              int v;mak[u]=true;
              ++point;
              do{//Find the bi-connected component of each point
                 v=st[top--];
                 Tree::add(v,point);
                 Tree::add(point,v);
                 merge(point,v);     
              }while (v!=a[i]);
              Tree::add(u,point);
              Tree::add(point,u);
              merge(point,u);
          }
      }else if (a[i]!=fa) low[u]=min(low[u],w[a[i]]);
}
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for (int i=1;i<=n;i++) scanf("%d",&val[i]);
    for (int i=1;i<=m;i++){
        int x,y;scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    point=n;Tarjan(1,0,1);
    for (int i=1;i<=n;i++)
      if (mak[i]==true)
        for (int j=p[i];j!=0;j=nxt[j])
          if (mak[a[j]]==true&&find(i)!=find(a[j])){
              ++point;
              Tree::add(point,i);Tree::add(i,point);
              Tree::add(point,a[j]);Tree::add(a[j],point);
          }
    for (int i=1;i<=n;i++)
      Tree::val[i]=val[i];
    Tree::BuildTree(point);
    for (int i=1;i<=q;i++){
        char c=getchar();
        int x,y;
        while (c!='A'&&c!='C') c=getchar();
        scanf("%d%d",&x,&y);
        if (c=='A') printf("%d\n",Tree::Query(x,y));
        else Tree::Change(x,y);
    }
    return 0;
}

Supplementary Notes on the Final Appearance

For dealing with the problem of point-to-point dual-connected components, because cut points belong to multiple points at the same time, this tree-building model can simplify the processing of cut points, so it seems to be a very common method.