Code implementation of AES encryption algorithm
Job objectives
The AES encryption algorithm is implemented in C language and optimized to the fastest speed.
Algorithm description
Introduction to AES
AES (Advanced Encryption Standard) is the most common symmetric encryption algorithm, also known as Rijndael encryption method. It is a block encryption standard adopted by the federal government of the United States.
Symmetric encryption algorithm: encryption and decryption use the same key. The encryption key can be calculated from the decryption key, and the decryption key can also be calculated from the encryption key.
Symmetric encryption algorithm is characterized by open algorithm, small amount of calculation, fast encryption speed and high encryption efficiency.
- Overall process
In the symmetric encryption algorithm, the data sender changes the plaintext (original data) and encryption key (mi yao) into complex encrypted ciphertext after being processed by a special encryption algorithm. After receiving the ciphertext, if the recipient wants to interpret the original text, it needs to decrypt the ciphertext using the encryption key and the inverse algorithm of the same algorithm to restore it to readable plaintext. As shown in the figure below:
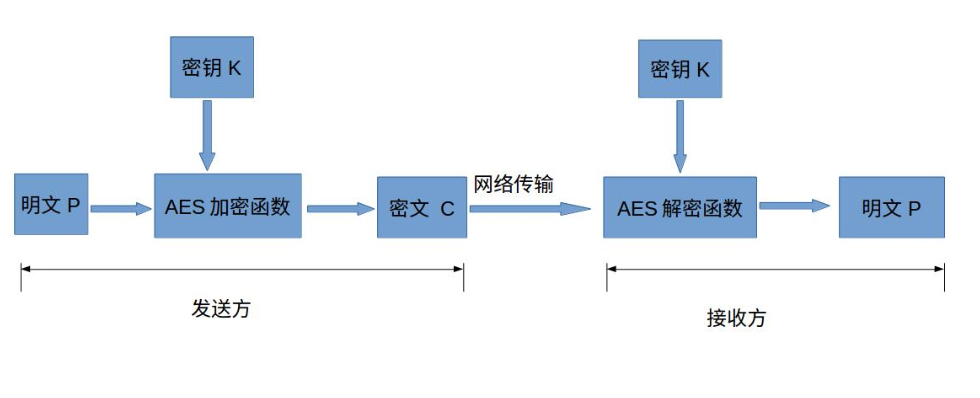
- Encryption process
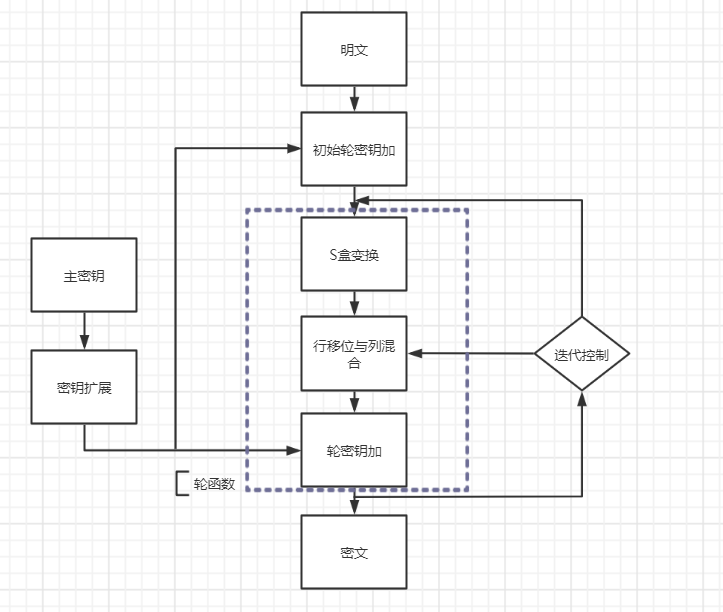
The wheel function in the figure consists of three layers:- The first layer is the S-box transform ByteSub, which is a nonlinear character transform with__ Confusion__ effect
- The second layer is the row shift transform ShiftRow + column mixed transform MixColumn to ensure the height above multiple rounds__ Spread__
- The third layer is the round key plus transformation AddRoundKey, which simply XOR the round key to the intermediate state to realize the encryption of the key__ Encryption control__ effect
Note: you can see that the last transformation points to the second layer without column mixing
- Decryption process
Similar to encryption, as shown below:
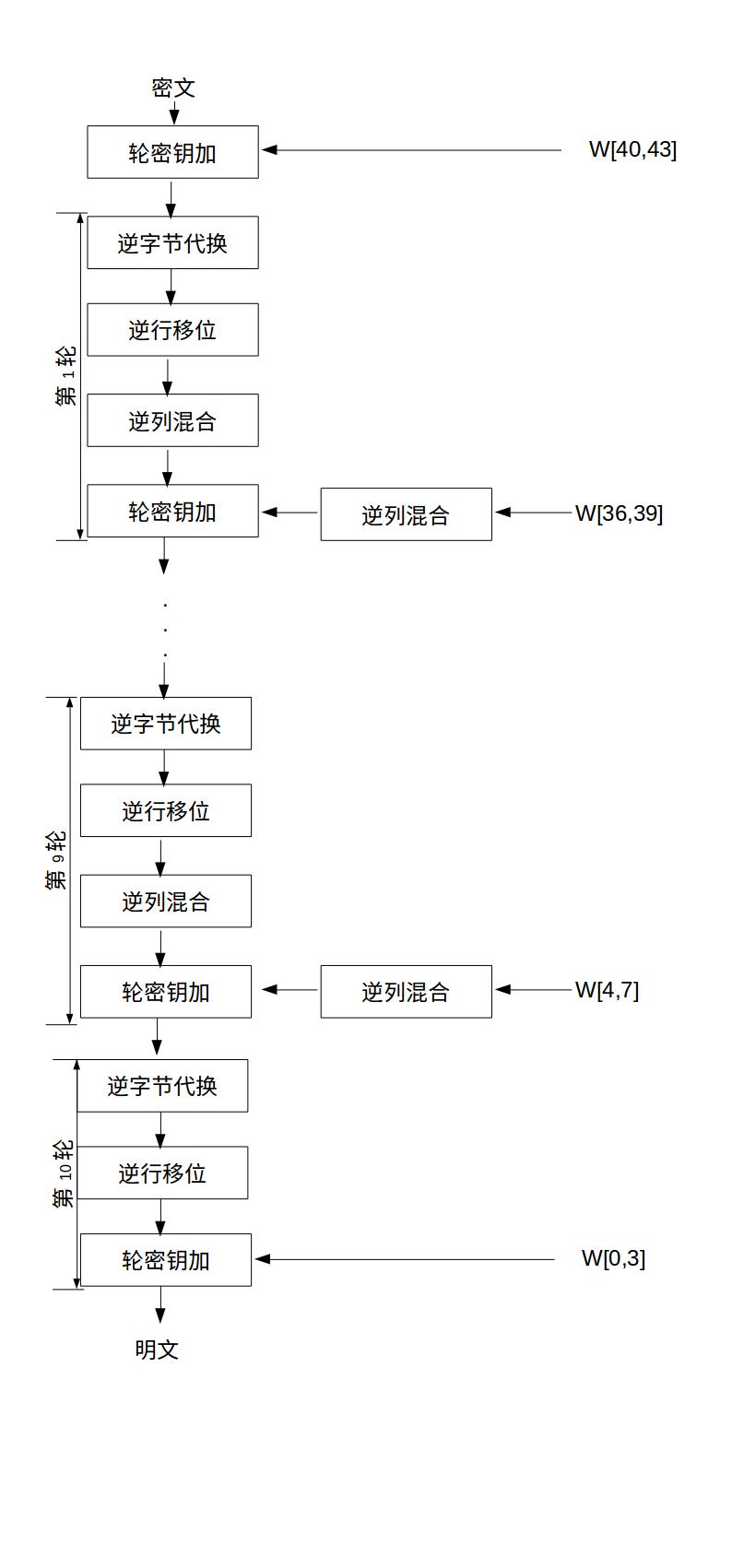
experimental design
- Required constants:
- The array defines the S-box and the inverse of the S-box
- Wheel constant to prevent the similarity of wheel keys of different wheels
- Column mixing (encryption); Inverse column mixing (decryption)
- Required function
- Bytes instead of SubBytes
- Replace InvSubBytes with inverse bytes
- Line shift and reverse shift ShiftRows
- Column mix MixColumns
- Inverse column mixing InvMixColumns
- Key plus AddRoundKey
- Key expansion
- Get round key GetRoundKey
- Encryption function Encrypt (call byte substitution, row shift, column mixing, key addition, key extension, get round key)
- Decrypt function decrypt (call inverse byte substitution, reverse shift, inverse column mixing, key encryption, key extension, and obtain round key)
- Main function main
- Call x(): control the flow to facilitate recursive use
S-box and S-box reverse
Define with sequence:
int s_box[256] =
{ 0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16};
int Invers_box[256] =
{ 0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D};
Byte replacement and inverse byte replacement
void SubBytes(int a[4][4],int s_box[256])
{
int i,j;
for (i = 0; i < 4; i++){
for (j = 0; j < 4; j++){
a[i][j] =s_box[a[i][j]];
}
}
}
As you can see, array A is the plaintext we input to be encrypted. Replace the number on each bit in a with the number in box S, that is, complete the conversion.
void InvSubBytes(int a[4][4],int InverS_box[256])/* InverS_box[256]It's an inverse S-box*/
{
int i,j;
for (i = 0; i < 4; i++)
for (j = 0; j < 4; j++)
a[i][j] = InverS_box [a[i][j]];
}
Line shift and retrograde shift
void ShiftRows(int a[4][4],int decrypt)
Use the variable decrypt. When encrypting, decrypt = 0 and shift the line; When decrypting, decrypt = 1 and perform reverse shift.
Realize the encryption line shift function
if(decrypt==0){
/* At this time, the encrypted line shift function is realized */
for(i=1;i<4;i++) {
if(i==1){
j=a[i][0];
a[i][0]=a[i][1];
a[i][1]=a[i][2];
a[i][2]=a[i][3];
a[i][3]=j;}
if(i==2){
j=a[i][0];
b=a[i][1];
a[i][0]=a[i][2];
a[i][1]=a[i][3];
a[i][2]=j;
a[i][3]=b;}
if(i==3){
j= a[i][3];
a[i][3]=a[i][2];
a[i][2]=a[i][1];
a[i][1]=a[i][0];
a[i][0]=j;}
}
}
It's easy to see that the first row doesn't move. Move the number corresponding to each column of rows 2, 3 and 4 to the right by 1, 2 and 3 bits. As shown in the figure below:
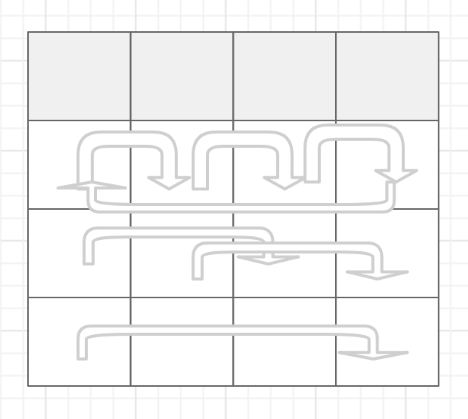
Decryption reverse shift function
if(decrypt==1) {
/* At this time, the decryption reverse shift function is realized */
for(i=1;i<4;i++) {
if(i==1){
j=a[i][3];
a[i][3]=a[i][2];
a[i][2]=a[i][1];
a[i][1]=a[i][0];
a[i][0]=j;}
if(i==2){
j=a[i][0];
b=a[i][1];
a[i][0]=a[i][2];
a[i][1]=a[i][3];
a[i][2]=j;
a[i][3]=b;}
if(i==3){
j=a[i][0];
a[i][0]=a[i][1];
a[i][1]=a[i][2];
a[i][2]=a[i][3];
a[i][3]=j;}
}
}
The decrypted line shift is the reverse of the same principle and then back
Column mixing and column inverse mixing
In AES algorithm, modular polynomial m(x)=x8+x4+x^3+x+1 is required. Column mixing is to multiply a constant matrix by the matrix transformed in the second step, so that each element in the matrix is the weighted sum of all elements in the original column of the element. As shown in the figure below:
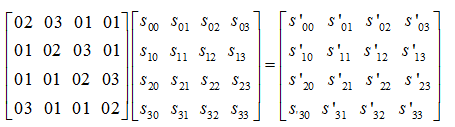
c(x) = 0x03*x^3 + 0x01*x^2 + 0x01*x + 0x02
01=1
02 = x
03 = x + 1
b[4][4] is the fixed matrix when columns are mixed
int b[4][4]={0x02,0x03,0x01,0x01,
0x01,0x02,0x03,0x01,
0x01,0x01,0x02,0x03,
0x03,0x01,0x01,0x02};
Column mixing concrete function
void MixColumns(int a[4][4],int b[4][4]) /*b[4][4]Fixed matrix when columns are mixed*/
{
int temp[4][4]={0};
int d[3]={0x80,0x1B,0x02};
int i,j,m,k;
for(m=0;m<4;m++){
for (i = 0; i<4;i++){
for (j = 0;j<4;j++){
if(b[i][j]==1)
temp[i][m]=a[j][m]^temp[i][m];
else {
if(b[i][j]==2){
if(a[j][m]<d[0]){
temp[i][m]=(b[i][j]*a[j][m])^temp[i][m];
}
else{
k=a[j][m]^d[0];
temp[i][m]=((b[i][j]*k)^d[1])^temp[i][m];
}
}
else{
if(a[j][m]<d[0])
temp[i][m]=((a[j][m]*d[2])^a[j][m])^temp[i][m];
else{
k=a[j][m]^d[0];
temp[i][m]=(((k*d[2])^d[1])^a[j][m])^temp[i][m];
}
}
}
}
}
}
for(i=0;i<4;i++)
for(j=0;j<4;j++)
a[i][j]=temp[i][j];
}
Use matrix multiplication, multiply the corresponding positions, and then add. Note that addition is an XOR operation.
First, declare a blank temp matrix, temporarily store the results of each step in the calculation, and import the final results into a
int d[3]={0x80,0x1B,0x02} is an array used to realize x multiplication, which is used to judge the processing overflow and carry
Reverse column mixing during decryption is the same:
Column inverse matrix
int c[4][4]={0x0E,0x0B,0x0D,0x09,
0x09,0x0E,0x0B,0x0D,
0x0D,0x09,0x0E,0x0B,
0x0B,0x0D,0x09,0x0E};
Column inverse mixed function
void InvMixColumns(int a[4][4],int c[4][4]) /*c[4][4]Is a fixed matrix when the inverse column is mixed*/
{
int temp[4][4]={0};
int d[7]={0x80,0x1B,0x02,0x0e,0x0b,0x0d,0x09};
int i,j,m,n,e,k,p,q,x,y;
for(m = 0;m < 4;m++)
for (i = 0; i < 4;i++)
for (j = 0;j < 4;j++){
e=a[j][m];y=a[j][m];
if(c[i][j]==d[3]){
for(n=0;n<3;n++){
if(y<d[0])
y=y*d[2];
else{
k=y^d[0];
y=(k*d[2])^d[1];}
if(n==0)
{p=y;}
else
if(n==1)
{q=y;}
else
{ x=y;}
}
temp[i][m]=p^q^x^temp[i][m];}
if(c[i][j]==d[4])
{for(n=0;n<3;n++)
{
if(y<d[0])
y=y*d[2];
else
{k=y^d[0];
y=(k*d[2])^d[1];}
if(n==0)
q=y;
if(n==2)
x=y;}
temp[i][m]=e^q^x^temp[i][m];}
if(c[i][j]==d[5])
{for(n=0;n<3;n++)
{
if(y<d[0])
y=y*d[2];
else
{k=y^d[0];
y=(k*d[2])^d[1];}
if(n==1)
q=y;
if(n==2)
x=y;}
temp[i][m]=e^q^x^temp[i][m];}
if(c[i][j]==d[6]){
for(n=0;n<3;n++){
if(y<d[0])
y=y*d[2];
else{
k=y^d[0];
y=(k*d[2])^d[1];}
}
temp[i][m]=e^y^temp[i][m];
}
}
for(i=0;i<4;i++)
for(j=0;j<4;j++)
a[i][j]=temp[i][j];
}
Key extension
void KeyExpansion(int roundkey[4][4],int s_box[256], int temp[4][44])
{
int i,j,n,m,a,b,x,y;
int w[4],r[4],q[4];
for(i=0;i<4;i++)
for(j=0;j<4;j++)
{temp[i][j]= roundkey[i][j];}
for(i=4;i<44;i++){
a=i-4;b=i-1;
if(i%4!=0){/*i Not a multiple of 4*/
for(j=0;j<4;j++)
q[j]=temp[j][a]^temp[j][b];
for(y=0;y<4;y++)
temp[y][i]=q[y];
}
else{ /*i Is a multiple of 4*/
for(x=0;x<4;x++)
w[x]=temp[x][b];
n=w[0]; /*Shift left one bit*/
w[0]= w[1];
w[1]= w[2];
w[2]= w[3];
w[3]=n;
for(j=0;j<4;j++)
w[j]=s_box[w[j]];/*Byte substitution*/
w[0]= rcon[(i-4)/4]^w[0];
for(m=0;m<4;m++)
r[m]=temp[m][a]^w[m];
for(y=0;y<4;y++)
temp[y][i]=r[y];
}
}
}
AES first inputs the initial key into a 44 state matrix. The four bytes in each column of the 44 matrix form a word. The four words in the four columns of the matrix are named W[0], W[1], W[2] and W[3], which form an array W in word units.
Then, 40 new columns are extended to the W array to form an extended key array with a total of 44 columns. The new column is generated according to the following rules:
- If i is not a multiple of 4, column i is determined by the following equation:
W[i]=W[i-4]⨁W[i-1] - If i is a multiple of 4, then column i is determined by the following equation:
W[i]=W[i-4]⨁T(W[i-1])
Where T is a somewhat complex function.
Function T consists of three parts: word loop, byte substitution and round constant XOR. The functions of these three parts are as follows.- a. Word cycle: cycle the 4 bytes in a word by 1 byte to the left. That is, the input word [b0, b1, b2, b3] is transformed into [b1,b2,b3,b0].
- b. Byte substitution: use S-box to substitute bytes for the result of word cycle.
- c. Round constant XOR: XOR the results of the first two steps with the round constant Rcon[j], where j represents the number of rounds.
The normal quantities are as follows:
The final 4-fold bits are encrypted by S-box enhancement, while other bits only depend on the XOR of the previous bit and the corresponding bit of the previous round./*Wheel constant to prevent the similarity of wheel keys of different wheels*/ const int rcon[10]={0x01,0x02,0x04, 0x08,0x10,0x20,0x40, 0x80,0x1B,0x36};
Get round key
/*Get round key*/
void GetRoundKey(int roundKey[4][4], int temp[4][44],int n)
{
int i,j;
for(i=0;i<4;i++)
for(j=0;j<4;j++)
roundKey[i][j]=temp[i][j+4*n];
}
Key addition
void AddRoundKey(int a[4][4],int roundKey[4][4])
{
int i,j;
for (i = 0;i < 4; i++)
for (j = 0; j < 4; j++)
a[i][j] = a[i][j] ^ roundKey[i][j];
}
Round key addition is a bit by bit XOR operation of the 128 bit round key Ki with the data in the state matrix
Note: the inverse operation of round key addition is completely consistent with the forward round key addition, because the inverse operation of XOR is itself. Round key addition is very simple, but it can affect every bit in the S array.
Encryption function
void Encrypt(int a[4][4],int roundKey[4][4],int temp[4][44])
{
int i,j,n;
int decrypt = 0;
AddRoundKey(a,roundKey);/* Round key addition*/
for(n=1;n<=10;n++)
{
if(n==10){
SubBytes(a,s_box); /* Byte substitution*/
ShiftRows(a,decrypt); /*Row shift*/
GetRoundKey(roundKey,temp,n); /* Get round key*/
AddRoundKey(a,roundKey); /* Round key addition*/
}
else{
SubBytes(a,s_box); /* Byte substitution*/
ShiftRows(a,decrypt); /*Row shift*/
MixColumns(a,b); /* Column mixing*/
GetRoundKey(roundKey,temp,n); /* Get round key*/
AddRoundKey(a,roundKey); /* Round key addition*/
}
}
}
Remove the displayed prompt information to send the line, which is the flow chart drawn before, and distinguish that there is no column mixing in the last round
Note: decrypt = 0 indicates encryption
Decryption function
Similar to encryption function
void Decrypt(int a[4][4],int roundKey[4][4],int temp[4][44])
{
int i,j,n,m;
int decrypt = 1;
int r[10]={0,9,8,7,6,5,4,3,2,1};
m=10;
GetRoundKey(roundKey, temp,m);
AddRoundKey(a,roundKey);
for(n=1;n<=10;n++) {
if(n==10)
{ ShiftRows(a,decrypt);
InvSubBytes(a,Invers_box);
m=0;
GetRoundKey(roundKey,temp,m);
AddRoundKey(a,roundKey);
}
else{
ShiftRows(a,decrypt);
InvSubBytes(a,Invers_box);
m=r[n];
GetRoundKey(roundKey, temp,m);
AddRoundKey(a,roundKey);
InvMixColumns(a,c);
}
}
}
Note that the reverse order is required to obtain the round key
m = 10 -n, each operation should not be as fast as creating an array table.
Process function (x)
-
Control flow, convenient for recursive use
-
Enter plaintext and initial key for initial encryption
-
Enter the initial key (Note: 32 characters are required, and each character must be between 0-a, otherwise an error will occur), and convert it into a hexadecimal matrix
scanf("%s",k); for(j=0;j<32;j++) { if(k[j]!='\0'&&k[j]<='f') if(k[j]<'a') l[j]=k[j]-'0'; else l[j]=10+(k[j]-'a'); else { printf(" Input error\n"); x(); }} for(n=0;n<32;n=n+2){ m=n/2; l[m]=l[n]*16+l[n+1]; } for(i=0;i<4;i++) for(j=0;j<4;j++) key[j][i]=l[j+i*4];Extended encryption required
KeyExpansion(key,s_box,Temp); Decrypt(w,key,Temp); x();
- Input plaintext block (Note: 32 characters are required, and each character must be between 0-a, otherwise an error occurs, and the check is similar)
for(i=0;i<32;i++) p[i]='0'; scanf("%s",o);//char o[32] for(i=0;o[i]!='\0';i++) p[i]=o[i]; for(i=0;i<32;i++){ if(p[i]!='\0'&&p[i]<='f') if(p[i]<'a') s[i]=p[i]-'0'; else s[i]=10+(p[i]-'a'); else{ printf(" Input error\n"); x(); } for(n=0;n<32;n=n+2){ m=n/2; s[m]=s[n]*16+s[n+1];//int s[32] } for(i=0;i<4;i++) for(j=0;j<4;j++) w[j][i]=s[j+i*4];Convert the input characters (0-10 string, such as' 123a ') one by one into numbers (such as' 1', '2', '3', '10'), then spell the two digits into hexadecimal numbers (such as' 0x12 (16 + 2) '0x3a (3 * 16 + 10)), and finally put int s[16] into int w[4][4] by column.
-
Optimization skills
Break the input limit and add time calculation
Originally, 32 characters were input, and each character must be between 0-a. otherwise, we will delete them directly, write a function to import the encrypted file, convert the file content into ascii code, and slice the content into 128 bits of the required size ()
if (fp != NULL) {
while ((ch = fgetc(fp)) != EOF){
s[num % 16] = (uint8_t)ch;
for(i=0;i<4;i++)
for(j=0;j<4;j++)
w[j][i]=(int)s[j+i*4];
if (num != 0 && num % 16 == 0) {
ftime(&ts1);
KeyExpansion(key,s_box,Temp);
Encrypt(w,key,Temp);
ftime(&ts2);
t_sec = ts2.time - ts1.time;
t_ms = ts2.millitm - ts1.millitm;
ti += t_sec * 1000 + t_ms;
}
num++;
}
}
At present, only the encryption part has been rewritten
S-box look-up table
Using the look-up table method can greatly improve the encryption speed
int s_box[256] = [...]
Column hybrid optimization
It is more convenient to use fixed matrix multiplication
int b[4][4]={0x02,0x03,0x01,0x01,
0x01,0x02,0x03,0x01,
0x01,0x01,0x02,0x03,
0x03,0x01,0x01,0x02};
The mixed column lookup table is not implemented. Put a target reference (the table is as follows:)
reference resources: https://gitee.com/lee_ka/AES/blob/master/1gai.cpp
unsigned char L_box(int i,unsigned char j)
{
return L_boxx[i][j];
}
static void MixColumns(unsigned char *col)//Column mixing
{
unsigned char tmp[4],xt[4];
int i;
for(i=0;i<4;i++,col+=4) //Col represents the base address of one column, col+4: the base address of the next column
{
tmp[0]=L_box(1,col[0])^L_box(2,col[1])^col[2]^col[3];
tmp[1]=col[0]^L_box(1,col[1])^L_box(2,col[2])^col[3];
tmp[2]=col[0]^col[1]^L_box(1,col[2])^L_box(2,col[3]);
tmp[3]=L_box(2,col[0])^col[1]^col[2]^L_box(1,col[3]);
//The modified value is directly modified on the original matrix
col[0]=tmp[0];
col[1]=tmp[1];
col[2]=tmp[2];
col[3]=tmp[3];
}
}
Transpose input
AES data is input by column, which is inconvenient to operate in the computer. After AES is transposed, data can be input by row. In this way, the forced type conversion of pointer can be used to reduce the cycle. Note that some operations after transposition also need to be transposed, including row shift and column confusion (see row shift and column confusion code), See - AES transpose implementation for the transpose implementation of AES. Note that after forcibly converting the pointer, the bytes inside int will be inverted.
for(i=0;i<4;i++) for(j=0;j<4;j++) w[j][i]=(int)s[j+i*4];
Function expression is clearer (not changed)
unsigned char xtime(unsigned char st)
{
return (st<<1)^((st&0x80)?0x1b:0x00);
//Shift the binary string of X multiplication by one bit to the left to judge whether the highest bit overflows. The overflow should be XOR 0x1b
}
void mixcolumns(unsigned char state[4][4],unsigned char cipher[4][4])
{
for(int j=0;j<4;j++)
{
for(int i=0;i<4;i++)
{
cipher[i][j]=
xtime(state[i%4][j]) //0x02 multiplication
^(state[(i+1)%4][j])^xtime(state[(i+1)%4][j])//0x03 multiplication
^state[(i+2)%4][j] //0x01 multiplication
^state[(i+3)%4][j]; //0x01 multiplication
}
}
}
Experimental results and reflection
experimental result
2963 ms v = 3538.89976 Byte/ms

summary
This experiment realized the text encryption by AES, deeply studied the use process and encryption process of AES algorithm, encountered many difficulties in column confusion and encryption key, had a deeper understanding of matrix multiplication and XOR operation, and thought of many optimization methods. Due to time constraints, the optimization has not been fully completed: column hybrid table lookup is not implemented; Column confusion the matrix multiplication code there looks a little confused. Maybe you can add a function call to make it easier to read; The encrypted new file was not saved and decrypted.
Complete code
See compression package
Remarks: aes_1: There is decryption, but the input is limited.
aes_2: For testing, you can encrypt files.