Look at the original topic. Please stamp below.
No more details about the topic. Look at the pictures.
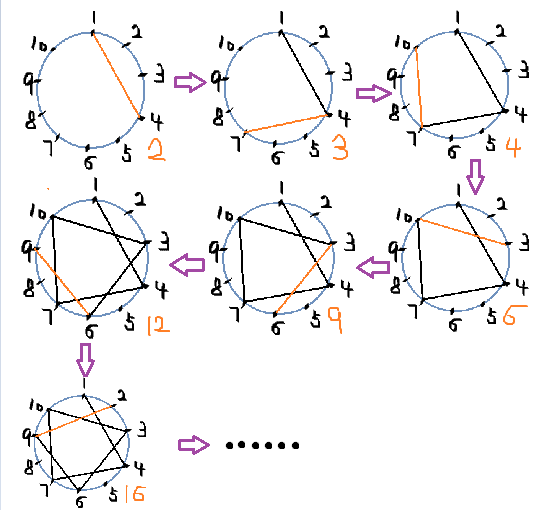
If index is the current point, index+k is the end point.
It is not difficult to see that the increment is the sum of the number of lines at all points between the two points plus 1.
Because of the large data range and the time-out of violence, the tree array is used to solve the problem. If you don't have a tree array, you can poke it here. ~ Tree Array Explanation~
In addition, a convex n-polygon with an increment of K and an increment of (n-k) yields the same result, which is not proved here.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
#include <vector>
#include <map>
#include <iomanip>
using namespace std;
long long v[1000010];
long long c[1000010];
long long C(int i)
{
long long temp = 0;
int index = i + 1 - (i&(-i));
while(index <= i)
{
temp+=v[index];
index++;
}
return temp;
}
long long SUM(int i)
{
long long s = 0;
while(i>0)
{
s+=c[i];
i -= (i&(-i));
}
return s;
}
void Update(int i,int add,int SIZE)
{
while(i<=SIZE)
{
c[i] += add;
i += (i&(-i));
}
}
int main()
{
int n,k;
while(cin>>n>>k)
{
memset(v,0,sizeof(v));
k=min(k,n-k);
for(int i=1; i<=n; i++)
{
if(i == 1||i == k+1)
v[i] = 1;
else
v[i] = 0;
c[i] = C(i);
}
cout<<"2";
int index = k+1;
long long tempsum = 2;
for(int i=2; i<=n; i++)
{
if(index+k>n)
{
tempsum += SUM(n) - SUM(index);
tempsum += SUM((index+k)-n-1);
tempsum++;
Update(index,1,n);
index = (index+k)-n;
Update(index,1,n);
}
else
{
tempsum += SUM(index+k-1) - SUM(index);
tempsum++;
Update(index,1,n);
index = (index+k);
Update(index,1,n);
}
cout<<" "<<tempsum;
}
cout<<endl;
}
}