Code clipping algorithm for line segment
For example, many uneven straight-line segments are distributed on a canvas, and we want to find a rectangular window on the canvas and only want to get the straight-line segments in the rectangular window. How should we achieve this?
We know that the straight line segment can be expressed by a parametric equation, assuming that the two endpoints of the straight line segment are (x1,y1), (x2,y2). The parameter equation of the straight line segment can be written as (x-x1) / (x2-x1) =(y-y1)/(y2-y1)=t. at this time, the range of t is [0,1]
The first step is to judge whether a straight line segment will intersect the rectangular window. For a straight line segment, its slope k is known. Set a straight line L: y=k*x+b, let l pass through the four vertices of the window, and get four intercepts. Record the maximum slope bit bmax and the minimum slope is bmin. For a straight line segment in the canvas, first judge whether its slope is between [bmin,bmax]. If not, directly remove the straight line.
If so, consider an idea. With the window as the center, the canvas is divided into 9 areas. The area inside the window is marked as 0 and the area outside the window is marked as 1. Mark the end point of the straight line segment. If the end point is in that area, it will be marked with the mark of the corresponding area.
Suppose the endpoint of the line segment is marked P,Q. If P|Q=0, it means that the straight line segment is in the window and is directly retained. Otherwise, if P & Q = 1, it indicates that there are two intersections with the window and one intersection with the straight line in other cases. The four edges of the rectangular window can also be expressed by parametric equation. Let the straight line segment intersect the four edges in turn, and find the solution, that is, the intersection. Let the parameter of the straight line segment be t and the parameter of the window straight line be u. only when t and u satisfy t,u ∈ [0,1] at the same time is the intersection
The following is the program implementation code
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>Code clipping algorithm</title>
</head>
<script src="../Assignment 1/dat.gui.js"></script>
<script language="JavaScript">
//Properties of the window
var xl, xr, yb, yt;
var canvas, context;
//Stores the two endpoints of a line and their corresponding flag bits
var line = new Array();
function init() {
canvas = document.getElementById("output");
context = canvas.getContext("2d");
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
var controls = new function() {
this.draw=function(){
context.clearRect(0,0,window.innerWidth,window.innerHeight);
drawWindow();
drawLine();
}
this.cut = function() {
//Clip line segment
cutLine();
context.clearRect(0,0,window.innerWidth,window.innerHeight);
//Redescribe
drawWindow();
afterShow();
}
};
var gui=new dat.GUI();
gui.add(controls,'draw');
gui.add(controls,'cut');
drawWindow();
drawLine();
}
//Draw window
function drawWindow() {
//Set window parameters
xl = window.innerWidth / 4;
xr = 3 * window.innerWidth / 4;
yb = window.innerHeight / 4;
yt = window.innerHeight / 2;
context.beginPath();
context.moveTo(xl, yb);
context.lineTo(xl, yt);
context.lineTo(xr, yt);
context.lineTo(xr, yb);
context.closePath();
context.stroke();
}
//Draw four line segments corresponding to four cases
function drawLine() {
//Completely outside the window
line[0] = new Array();
line[0]["xb"] = window.innerWidth / 4;
line[0]["yb"] = window.innerHeight / 8;
line[0]["xg"] = window.innerWidth / 8;
line[0]["yg"] = window.innerHeight / 3;
line[0]["tagb"] = 0;
line[0]["tagg"] = 0;
line[0]["isprint"] = false;
//An intersection
line[1] = new Array();
line[1]["xb"] = window.innerWidth / 2;
line[1]["yb"] = window.innerHeight / 8;
line[1]["xg"] = 5 * window.innerWidth / 8;
line[1]["yg"] = 3 * window.innerHeight / 8;
line[1]["tagb"] = 0;
line[1]["tagg"] = 0;
line[1]["isprint"] = false;
//Completely within the window
line[2] = new Array();
line[2]["xb"] = 3 * window.innerWidth / 8;
line[2]["yb"] = 5 * window.innerHeight / 16;
line[2]["xg"] = 5 * window.innerWidth / 8;
line[2]["yg"] = 7 * window.innerHeight / 16;
line[2]["tagb"] = 0;
line[2]["tagg"] = 0;
line[2]["isprint"] = false;
//There are two intersections with the window
line[3] = new Array();
line[3]["xb"] = window.innerWidth / 8;
line[3]["yb"] = 3 * window.innerHeight / 8;
line[3]["xg"] = window.innerWidth / 2;
line[3]["yg"] = 5 * window.innerHeight / 8;
line[3]["tagb"] = 0;
line[3]["tagg"] = 0;
line[3]["isprint"] = false;
for (var i = 0; i < 4; i++) {
context.moveTo(line[i]["xb"], line[i]["yb"]);
context.lineTo(line[i]["xg"], line[i]["yg"]);
}
context.stroke();
SureTag();
}
//Mark both ends of the segment
function SureTag() {
for (var i = 0; i < 4; i++) {
line[i]["tagb"] = caculate(line[i]["xb"], line[i]["yb"]);
line[i]["tagg"] = caculate(line[i]["xg"], line[i]["yg"]);
}
}
//Here, 1 is not returned uniformly in the window
function caculate(x, y) {
if (x < xl) {
return 1;
} else if (x <= xr) {
if (y >= yb && y <= yt)
return 0;
else
return 1;
} else {
return 1;
}
}
//Code for clipping lines
function cutLine() {
var tline=new Array();
for (var i = 0; i < 4; i++) {
//The two endpoints are in the window
if ((line[i]["tagb"] || line[i]["tagg"]) == 0) {
line[i]["isprint"] = true;
}
else {
//Both endpoints are outside the window
//There may be no intersections, there may be two intersections, there may be one intersection
//No intersection and one intersection are treated as not in the window
if ((line[i]["tagb"] && line[i]["tagg"]) == 1){
//Not in window
if(judge(line[i])==false){
line[i]["isprint"]=false;
}
//In the window, cut out the middle segment
else{
tline=getCoor(line[i]);
line[i]["xb"]=tline["xb"];
line[i]["yb"]=tline["yb"];
line[i]["xg"]=tline["xg"];
line[i]["yg"]=tline["yg"];
line[i]["isprint"]=true;
}
}
//End point in window, crop
else if (line[i]["tagg"] == 0) {
tline=getCoor(line[i]);
line[i]["xb"]=tline["xb"];
line[i]["yb"]=tline["yb"];
line[i]["isprint"]=true;
}
//Start point in window, crop
else {
tline=getCoor(line[i]);
line[i]["xg"]=tline["xb"];
line[i]["yg"]=tline["yb"];
line[i]["isprint"]=true;
}
}
}
}
//Determine whether there is an intersection with the polygon
function judge(line){
var b=new Array();
var maxb=0;
var minb=0;
var lineb=0;
var k=(line["yg"]-line["yb"])/(line["xg"]-line["xb"]);
//The point oblique equation is obtained
//y=k*(x-line["xg"])+line["yg"]
//y=kx+b,b=y-kx
b[0]=new Array();
b[0]=yb-k*xl;
b[1]=new Array();
b[1]=yb-k*xr;
b[2]=new Array();
b[2]=yt-k*xr;
b[3]=new Array();
b[3]=yt-k*xl;
//Intersect with four vertices to find the range of intercept
maxb=Math.max(b[0],b[1],b[2],b[3]);
minb=Math.min(b[0],b[1],b[2],b[3]);
lineb=line["yg"]-k*line["xg"];
if(lineb>minb && lineb<maxb)
return true;
else
return false;
}
//Obtain the coordinates of the intersection, which can be one intersection or two intersections
function getCoor(line){
var tline=new Array();
tline["tag"]=0;
//What intersection is the record
//Get the parameter equation of the line, judge the range of t, and get the intersection with that edge
//y=(1-t)*yb+t*yg
//x=(1-t)*xb+t*xg
//Find the intersection with the four edges respectively
var t=0;
//y=yb
t=(yb-line["yb"])/(line["yg"]-line["yb"]);
if(t>=0 && t<=1){
tline["xb"]=(1-t)*line["xb"]+t*line["xg"];
tline["yb"]=yb;
tline["tag"]=1;
}
//y=yt
t=(yt-line["yb"])/(line["yg"]-line["yb"]);
if(t>=0 && t<=1){
if(tline["tag"]==0){
tline["xb"]=(1-t)*line["xb"]+t*line["xg"];
tline["yb"]=yt;
tline["tag"]=1;
}
else{
tline["xg"]=(1-t)*line["xb"]+t*line["xg"];
tline["yg"]=yt;
tline["tag"]=2;
//There are at most two intersections
return tline;
}
}
//x=xl
t=(xl-line["xb"])/(line["xg"]-line["xb"]);
if(t>=0&&t<=1){
if(tline["tag"]==0){
tline["xb"]=xl;
tline["yb"]=(1-t)*line["yb"]+t*line["yg"];
tline["tag"]=1;
}
else{
tline["xg"]=xl;
tline["yg"]=(1-t)*line["yb"]+t*line["yg"];
tline["tag"]=2;
//There are at most two intersections
return tline;
}
}
//x=xr
t=(xr-line["xb"])/(line["xg"]-line["xb"]);
if(t>=0&&t<=1){
if(tline["tag"]==0){
tline["xb"]=xr;
tline["yb"]=(1-t)*line["yb"]+t*line["yg"];
tline["tag"]=1;
}
else{
tline["xg"]=xr;
tline["yg"]=(1-t)*line["yb"]+t*line["yg"];
tline["tag"]=2;
//There are at most two intersections
return tline;
}
}
return tline;
}
function afterShow(){
for(var i=0;i<4;i++){
if(line[i]["isprint"]==true){
context.moveTo(line[i]["xb"],line[i]["yb"]);
context.lineTo(line[i]["xg"],line[i]["yg"]);
}
}
context.stroke();
}
window.onload = init;
</script>
<body>
<canvas id="output"></canvas>
</body>
</html>
Initial state
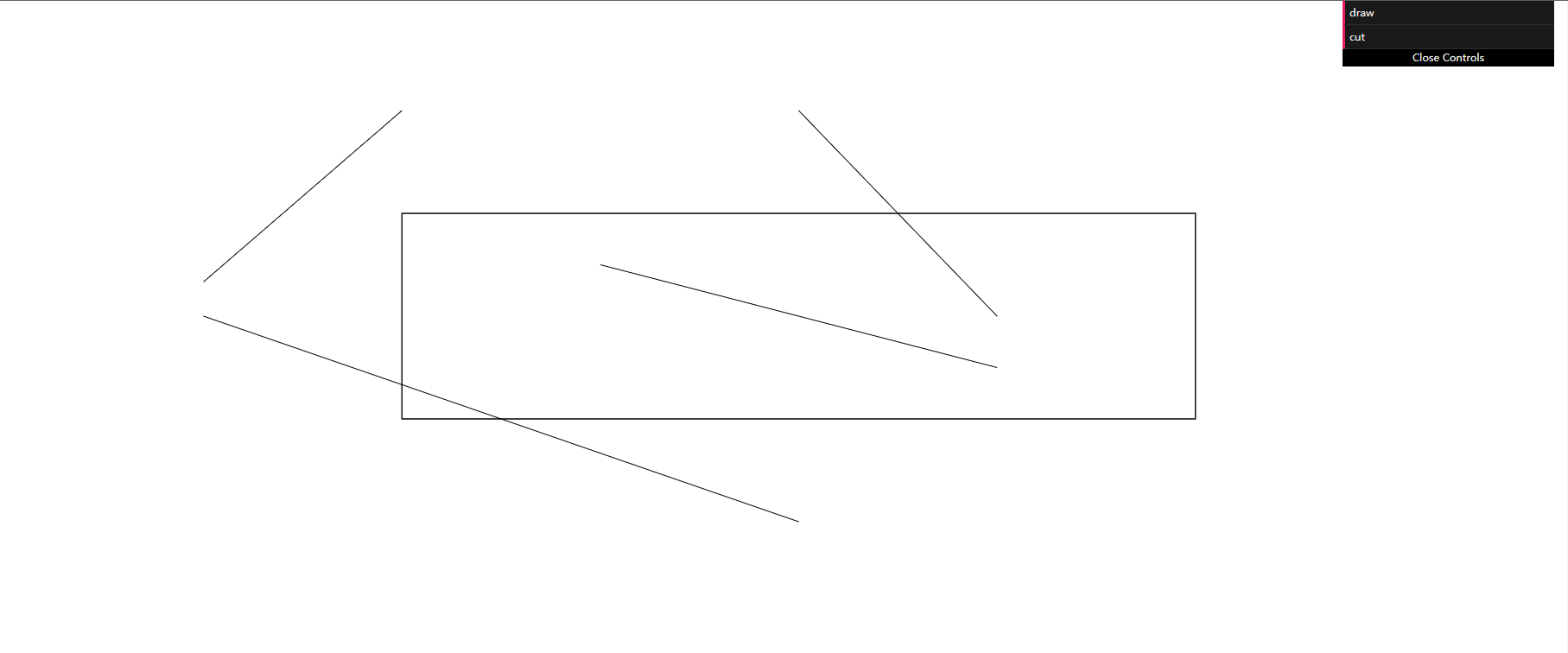
After clicking cut in the upper right corner
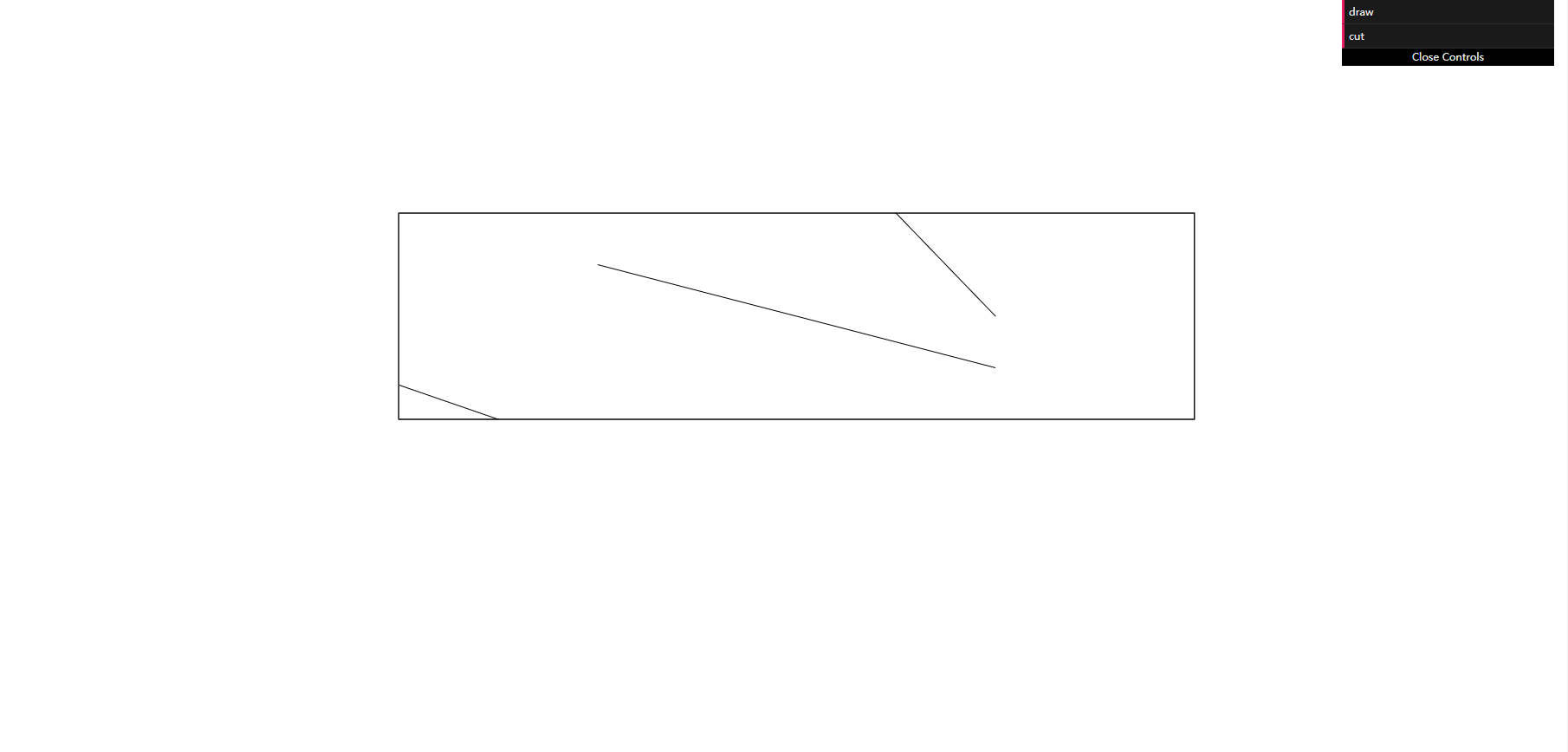
It can be seen that the code successfully cuts the straight line segment and retains the straight line segment in the window.