Merge sort

The classical divide and conquer strategy is used in merging and sorting. Divide an array into half parts all the time, and the scale of the problem will be reduced. Repeat the process until the number of elements is one, and one element will be arranged in order. Next, merge two elements and four elements in order.
The implementation code is as follows:

 public static void mergeSort(int[] array) {
       // Build a temporary array before sorting to avoid frequent space creation in recursion
       int[] temp = new int[array.length];
       mergeSort(array, 0, array.length - 1, temp);
   }

   public static void mergeSort(int[] array, int left, int right, int[] temp) {
       if (left < right) {
           int mid = (left + right) / 2;
           // Left recursive sorting makes left subsequence ordered
           mergeSort(array, left, mid, temp);
           // Recursive sorting on the right makes the right subsequence orderly
           mergeSort(array, mid + 1, right, temp);
           // Merge two ordered arrays
           merge(array, left, mid, right, temp);
       }
   }

   public static void merge(int[] array, int left, int mid, int right, int[] temp) {
       // Left sequence pointer
       int i = left;
       // Right sequence pointer
       int j = mid + 1;
       // Temporary array pointer
       int t = 0;
       while (i <= mid && j <= right) {
           if (array[i] < array[j])
               temp[t++] = array[i++];
           else
               temp[t++] = array[j++];
       }
       // Put the left sequence ascending element into temp
       while (i <= mid) {
           temp[t++] = array[i++];
       }
       // Put the right sequence ascending element into temp
       while (j <= right) {
           temp[t++] = array[j++];
       }
       t = 0;
       // Copy the sorted array into the original array
       while (left <= right) {
           array[left++] = temp[t++];
       }
   }

   public static void main(String[] args) {
       int[] array = {10, 7, 2, 4, 7, 62, 3, 4, 2, 1, 19};
       mergeSort(array);
       for (int i = 0; i < array.length; i++) {
           System.out.print(array[i] + " ");
       }
   }

The process diagram is as follows:

The merging sorting is stable, the average time complexity is O(nlogn), and the space complexity is O(n).

Heap sort

Heap sorting is an algorithm that regards data as a complete binary tree and sorts data according to the characteristics of the complete binary tree.
The maximum heap requires that no element of a node be less than its child. Then the element at the root node of the maximum heap must be the maximum value in the heap. The following figure shows a maximum heap, and the complete binary tree has one feature: left child node subscript = current parent node subscript * 2 + 1, right child node subscript = current parent node subscript * 2 + 1.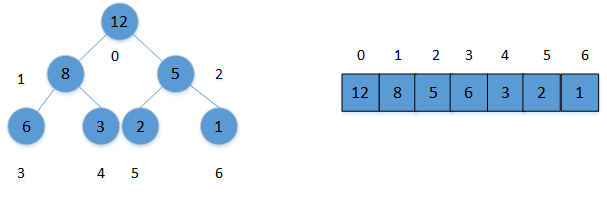

The process diagram of heap sorting is as follows:

The implementation process is as follows:

    public static void heapify(int[] arrays, int currentRootNode, int size) {
        if (currentRootNode < size) {
            //Left subtree and right word position
            int left = 2 * currentRootNode + 1;
            int right = 2 * currentRootNode + 2;

            //Consider the current parent node position as the largest
            int max = currentRootNode;

            if (left < size) {
                //If it is larger than the current root element, record its location
                if (arrays[max] < arrays[left]) { max = left; }
            }
            if (right < size) {
                //If it is larger than the current root element, record its location
                if (arrays[max] < arrays[right]) { max = right; }
            }
            //If the largest is not the root element position, swap
            if (max != currentRootNode) {
                int temp = arrays[max];
                arrays[max] = arrays[currentRootNode];
                arrays[currentRootNode] = temp;
                //Continue to compare until one build is completed
                heapify(arrays, max, size);
            }
        }
    }

    public static void maxHeapify(int[] arrays, int size) {
        // Start at the end of the array until the first element (angle is 0)
        for (int i = size - 1; i >= 0; i--) {
            heapify(arrays, i, size);
        }
    }

    public static void heapSort(int[] array){
        for (int i = 0; i < array.length; i++) {
            //Every time you build a heap, you can exclude one element
            maxHeapify(array, array.length - i);
            //exchange
            int temp = array[0];
            array[0] = array[(array.length - 1) - i];
            array[(array.length - 1) - i] = temp;
        }
    }

    public static void main(String[] args) {
        int[] array = {10, 7, 2, 4, 7, 62, 3, 4, 2, 1, 19};
        heapSort(array);
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + " ");
        }
    }