1. Bubble sorting idea

The idea of bubble sorting is to compare two numbers from the first number and exchange them in reverse order. After a comparison, the largest number will be exchanged to the last, that is, the largest number will sink to the bottom, which is similar to the largest bubble at the bottom of the pool (on the contrary, the principle of sorting from large to small is the same). Then repeat the above process for the first n-1 records until the sorting is completed, similar to the bubbling process.
  note: in a sort comparison, if no exchange is found between two comparisons, it indicates that the array has been ordered.

2. Algorithm steps of bubble sorting

(1) Take the sorting from small to large as an example: start from the first element and the second element, compare the two adjacent elements, and if the former is larger than the latter, exchange positions with each other, otherwise keep the original state.
(2) The second element is compared with the third element. If the second element is larger than the third element, change the position of each other, otherwise it remains the same.
(3) For each pair of adjacent elements, repeat the above process of "comparison" and "exchange" until the last pair of elements. At this time, the largest number has been exchanged to the end, that is, the largest bubble has emerged.
(note that the biggest bubble has already popped up, so you don't need to participate in the next sorting process of comparison and exchange. The next task is to make the next big bubble pop up.)
(4) Similarly, start the second round of comparison and exchange sorting process for all elements (except the largest number), and find the second largest bubble.
(5) Continue to repeat the above steps for fewer and fewer elements each time until the sorting is completed (no pair of numbers need to be compared).
(6) Note: in the process of sorting, if you find that there is no element to be exchanged in pairwise comparison, it means that the whole arrangement has been orderly and there is no need to compare the remaining two elements in the last round.


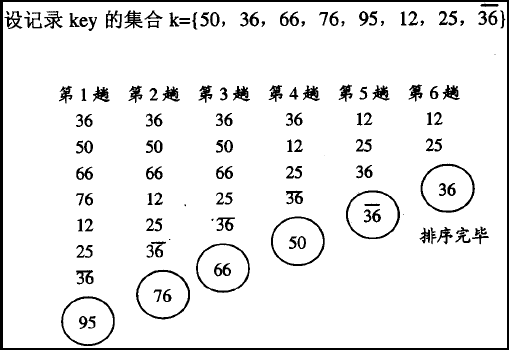
      as can be seen from the above figure, bubble sorting belongs to stable sorting.

3. Bubble sort code

# coding:utf-8
'''
# @Method: bubble sort
# @Author: wlhr62
'''
import os
import sys


class Solution:
    def BubbleSort(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        n = len(nums)
        for i in range(n):
            for j in range(0, n-i-1):
                if nums[j] > nums[j+1]:
                    # temp = nums[j]
                    # nums[j] = nums[j+1]
                    # nums[j+1] = temp
                    nums[j], nums[j+1] = nums[j+1], nums[j]
            print("The first", i+1, "Sorting result of round:", nums)
        return nums
        

if __name__ == "__main__":
    nums = [50, 36, 66, 76, 95, 12, 25, 36]
    A = Solution()
    res = A.BubbleSort(nums)
    print("Final sorting result:", res)
    

The running results of the code are as follows:

Sorting results of round 1: [36, 50, 66, 76, 12, 25, 36, 95]
Sorting results of round 2: [36, 50, 66, 12, 25, 36, 76, 95]
Sorting results of round 3: [36, 50, 12, 25, 36, 66, 76, 95]
Sorting results of round 4: [36, 12, 25, 36, 50, 66, 76, 95]
Sorting results of round 5: [12, 25, 36, 36, 50, 66, 76, 95]
Sorting results of round 6: [12, 25, 36, 36, 50, 66, 76, 95]
Sorting results of Round 7: [12, 25, 36, 36, 50, 66, 76, 95]
Sorting results of round 8: [12, 25, 36, 36, 50, 66, 76, 95]
Final sorting result: [12, 25, 36, 36, 50, 66, 76, 95]

Existing problems:
                       .
  don't forget the precautions mentioned above at the beginning: in a sort comparison, if no exchange is found between two comparisons, it indicates that the array is in order.

The modification code is as follows:
   add a tag variable to judge whether there is exchange in the current round of sorting. If not, the sorting process is ended directly.

# coding:utf-8
'''
# @Method: bubble sort
# @Author: wlhr62
'''
import os
import sys


class Solution:
    def BubbleSort(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        n = len(nums)
        for i in range(n):
            changeNum = 0  # Add a variable to judge whether there is exchange during this round of sorting
            for j in range(0, n-i-1):
                if nums[j] > nums[j+1]:
                    nums[j], nums[j+1] = nums[j+1], nums[j]
                    changeNum += 1
            print("The first", i+1, "Sorting result of round:", nums)
            # If it is found that there is no exchange between two comparisons, it indicates that the array has been ordered
            if changeNum == 0:
                break
        return nums
        

if __name__ == "__main__":
    nums = [50, 36, 66, 76, 95, 12, 25, 36]
    A = Solution()
    res = A.BubbleSort(nums)
    print("Final sorting result:", res)
    

The running results after modifying the code are as follows:

Sorting results of round 1: [36, 50, 66, 76, 12, 25, 36, 95]
Sorting results of round 2: [36, 50, 66, 12, 25, 36, 76, 95]
Sorting results of round 3: [36, 50, 12, 25, 36, 66, 76, 95]
Sorting results of round 4: [36, 12, 25, 36, 50, 66, 76, 95]
Sorting results of round 5: [12, 25, 36, 36, 50, 66, 76, 95]
Sorting results of round 6: [12, 25, 36, 36, 50, 66, 76, 95]
Final sorting result: [12, 25, 36, 36, 50, 66, 76, 95]

Think: can the repetition of round 6 be omitted?

4. Introduction and solution of bubble sorting algorithm

   see Introduction to algorithms exercise 2-2
   some minor optimizations can also be done. In many teaching materials, the internal circulation often adopts the way of reverse order to bubble the small number first. In this way, the end judgment condition of the inner loop can be changed to j > I to reduce one subtraction operation.

python code

# coding:utf-8
'''
# @Method: bubble sort
# @Author: wlhr62
'''
import os
import sys


class Solution:
    def BubbleSort(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        n = len(nums)
        for i in range(n):
            changeNum = 0  # Add a variable to judge whether there is exchange during this round of sorting
            for j in range(n-1, i, -1):
                if nums[j] < nums[j-1]:
                    nums[j], nums[j-1] = nums[j-1], nums[j]
                    changeNum += 1
            print("The first", i+1, "Sorting result of round:", nums)
            # If it is found that there is no exchange between two comparisons, it indicates that the array has been ordered
            if changeNum == 0:
                break
        return nums
        

if __name__ == "__main__":
    nums = [50, 36, 66, 76, 95, 12, 25, 36]
    A = Solution()
    res = A.BubbleSort(nums)
    print("Final sorting result:", res)

The running results of the code are as follows:

Sorting results of round 1: [12, 50, 36, 66, 76, 95, 25, 36]
Sorting results of round 2: [12, 25, 50, 36, 66, 76, 95, 36]
Sorting results of round 3: [12, 25, 36, 50, 36, 66, 76, 95]
Sorting results of round 4: [12, 25, 36, 36, 50, 66, 76, 95]
Sorting results of round 5: [12, 25, 36, 36, 50, 66, 76, 95]
Final sorting result: [12, 25, 36, 36, 50, 66, 76, 95]

5. Complexity analysis of bubble sorting

• Worst time complexity: O(n^2)
• Unless otherwise specified, the worst time complexity is generally calculated.
• In bubble sorting, the worst case is that the initial state of the list is completely in reverse order. In this case, n-1 rounds of bubbling are required, and each round of bubbling requires n-i-1 comparison and exchange operations. The average value of I is n/2 and the time complexity is n(n-1)/2.
• In the worst case, the time complexity of bubble sorting is O(n^2).
• Optimal time complexity: O(n)
• In bubble sorting, the best case is that the initial state of the list completely conforms to the expected arrangement. In this case, only one round of bubbling is required, and there is no comparison and exchange in this process. A marked variable is used to judge whether there is exchange in the current round of sorting. If not, the sorting process is ended directly.
• In the best case, the time complexity of bubble sorting is O(n).
• Average time complexity: O(n^2)
• In bubble sorting, the average time complexity is O(n^2).
• Space complexity: O(1)

6. Stability analysis of bubble sorting

• Bubble sort belongs to stable sort.
• Analysis: in bubble sorting, two elements are compared each time, and the exchange will be carried out only when the size order of the elements is wrong. If there are two equal elements in the element list, they will eventually be adjacent to each other, but the comparison is not in the wrong order, so they will not be exchanged during comparison, and the relative order remains unchanged. Therefore, bubble sorting is a stable sorting algorithm.