Classic interview questions of binary tree
Before that, I have published the basic knowledge of binary tree: Detailed explanation of binary tree Next, I will tell you some classic and common binary tree interview questions
Preliminary interview questions
Maximum depth of binary tree
Question: Maximum depth of binary tree
Solution idea: this problem can be realized by the simplest recursive method. For example, when the root node is empty, it returns 0. If not, it will continue to recurse its left child and right child;
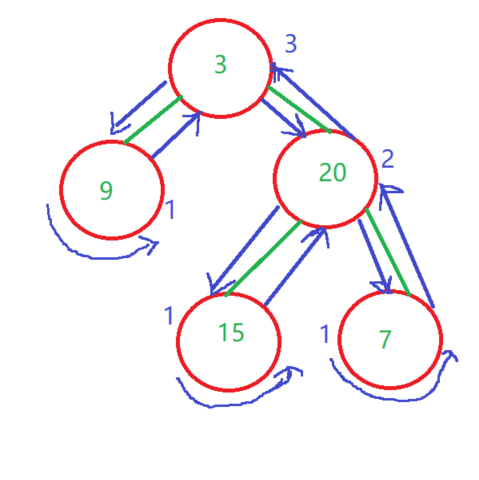
Recursion is shown in the figure below:
The code is as follows:
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
//If the node is empty, 0 is returned
return 0;
}
int leftDepth=maxDepth(root.left);//Recursive left child of the node
int rightDepth=maxDepth(root.right);//Recursive right child of the node
if(leftDepth>rightDepth){//Compare the left and right depths. Whoever is older will return its depth + 1;
return leftDepth+1;
}
return rightDepth+1;
}
}

The time complexity is O(n): where n is the number of nodes of the binary tree, and each node will be traversed once, and the space complexity is O(high): where high is the height of the binary tree, because each recursion needs to open up a stack space, and the development space of the stack depends on the depth of recursion.
balanced binary tree
balanced binary tree
Solution idea: it can be seen from the question that the absolute value of the height difference between the left and right subtrees of each node of the balanced binary tree does not exceed 1. Then we can use the recursive method to find the depth of the left subtree and the right subtree of the node, and then see whether the difference between the absolute values is less than or equal to 1.
The code is as follows:
class Solution {
public int maxDepth(TreeNode root){
if(root==null){
return 0;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
return Math.max(left,right)+1;
}
public boolean isBalanced(TreeNode root) {
if (root==null){
return true;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
if (Math.abs(left-right)<=1&&isBalanced(root.right)&&isBalanced(root.left)){
return true;
}
return false;
}
Its time complexity is O(n*n): n is the number of nodes of the binary tree.
The spatial complexity is O(n):n is the number of nodes in the binary tree. The spatial complexity mainly depends on the number of layers of recursive calls, and the number of layers of recursive calls will not exceed n.
In order to improve the efficiency of time complexity, a bottom-up recursive method can be used: this method first recursively judges whether the left and right subtrees are balanced, and finally judges whether the node is a balanced tree. If yes, the height is returned, otherwise, - 1 is returned
The code is as follows
class Solution {
public int maxDepth(TreeNode root){
if(root==null){
return 0;
}
int left=maxDepth(root.left);
int right=maxDepth(root.right);
if(left>=0&&right>=0&&Math.abs(left-right)<=1){
return Math.max(left,right)+1;
}
return -1;
}
public boolean isBalanced(TreeNode root){
return maxDepth(root)>=0;
}
}

The optimized time complexity is O(n)
Same tree
Same tree
Solution idea: the problem can be solved simply by using recursive method. First, we should judge whether the node is empty. 1. If p and q are empty, return true. 2. If only one tree of p and q is empty, return false. If the value of p is not equal to the value of q, return false.
The core code is as follows:
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null&&q==null){//Returns true if both P and Q are empty
return true;
}
if(p==null||q==null){//If only one tree of P and Q is empty, false is returned
return false;
}
if(p.val!=q.val){//p. The values of Q are not equal
return false;
}
if(isSameTree(p.left,q.left)&&isSameTree(p.right,q.right)){
//recursion
return true;
}
return false;
}
}
A subtree of another tree
A subtree of another tree
Solution idea: the solution method is roughly the same as that of the above question: the same tree, but first judge whether the root node of subRoot is the root node of root, the left child of root or the right child of root.
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null&&q!=null||p!=null&&q==null){
return false;
}
if(p==null&&q==null){
return true;
}
if(p.val!=q.val){
return false;
}
if(isSameTree(p.left,q.left)&&isSameTree(p.right,q.right))
{
return true;
}
return false;
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root==null){//Determine whether root is empty
return false;
}
if(isSameTree(root,subRoot)){
//Judge whether the root node of subRoot is the root node of root
return true;
}
if (isSubtree(root.left,subRoot)){
//Whether the root node of subRoot is the left child of root
return true;
}
if(isSubtree(root.right,subRoot)){
//Is the root node of subRoot the right child of root
return true;
}
return false;}
}
Symmetric binary tree
Symmetric binary tree

Problem solving idea: first judge whether the tree is empty, and then use the recursive method to judge whether the values of the left child and the right child are equal.
The code is as follows:
class Solution {
public boolean isSymmetricChild(TreeNode leftTree, TreeNode rightTree){
if(leftTree==null&&rightTree!=null||leftTree!=null&&rightTree==null){
return false;
}
if(leftTree==null&&rightTree==null){
return true;
}
if (leftTree.val!=rightTree.val){
return false;
}
return isSymmetricChild(leftTree.left,rightTree.right)&&isSymmetricChild(leftTree.right,rightTree.left);
}
public boolean isSymmetric(TreeNode root) {
if (root==null){
return false;
}
return isSymmetricChild(root.left,root.right);
}
}
Image of binary tree
Image of binary tree
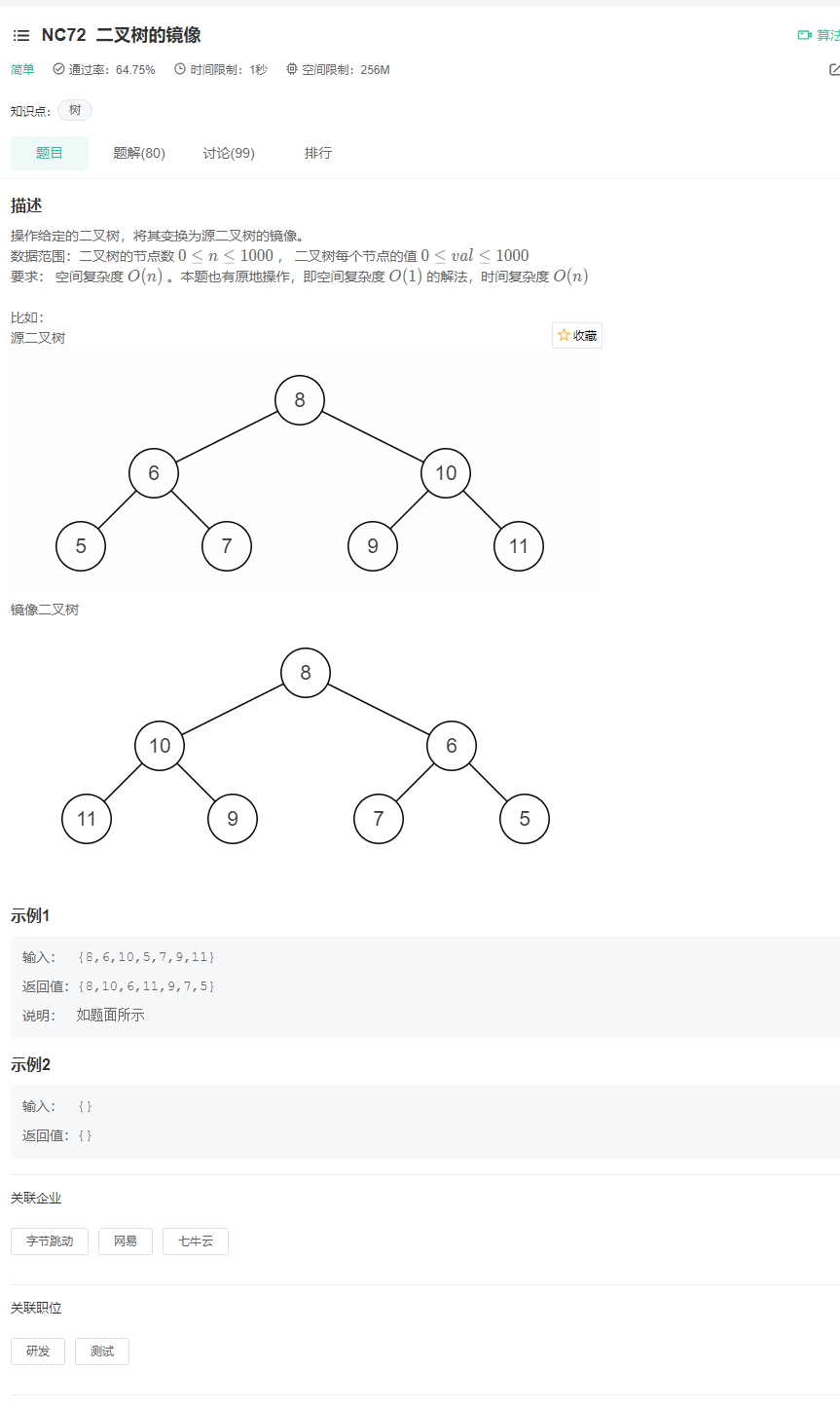
Problem solving ideas:
The code is as follows: using the recursive method, first judge whether the tree is empty, then use the recursive method to exchange the left and right subtrees, and finally return to the root node.
public class Solution {
/**
* The class name, method name and parameter name in the code have been specified. Do not modify them. Just return the value specified by the method directly
*
*
* @param pRoot TreeNode class
* @return TreeNode class
*/
public TreeNode Mirror (TreeNode pRoot) {
// write code here
if(pRoot==null){
return null;
}
TreeNode root=new TreeNode(pRoot.val);
root.left=Mirror(pRoot.right);
root.right=Mirror(pRoot.left);
return root;
}
}
Advanced surface test questions
Print binary tree into multiple lines
Print binary tree into multiple lines
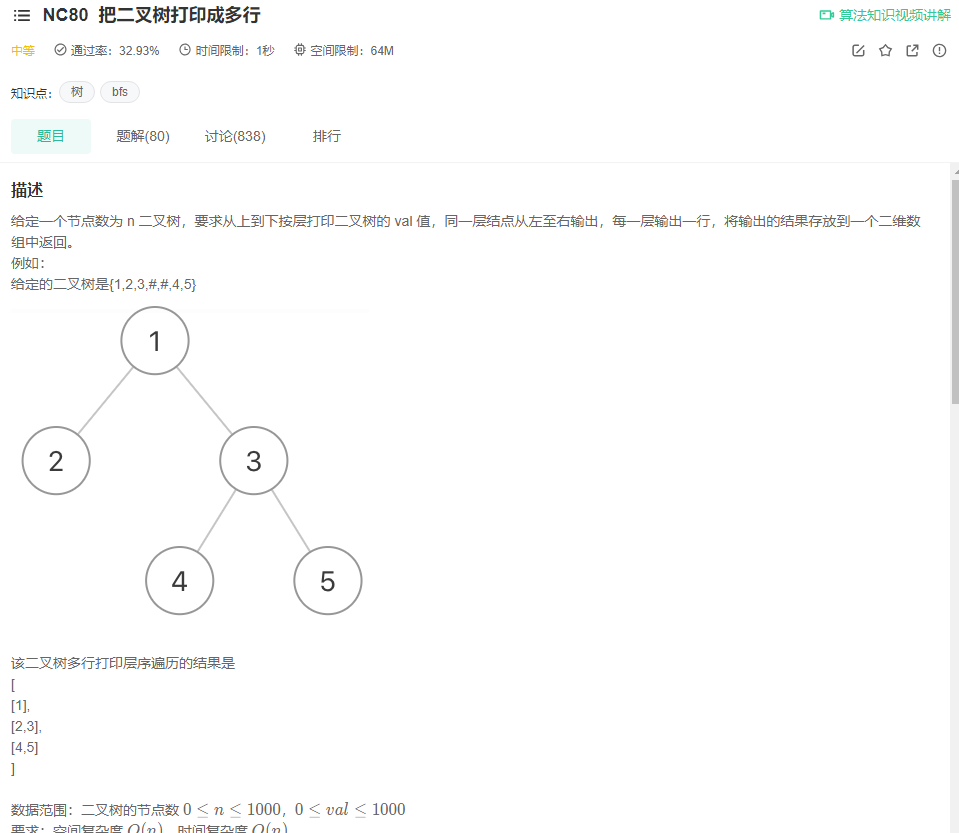
Solution idea: it can be seen from the question that its root is to let us traverse the binary tree hierarchically, so we need to use the queue. In order to print multiple lines, we need to put the traversed values into the set
The code is as follows:
import java.util.*;
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> list=new ArrayList<>();
if (pRoot==null){
return list;
}
TreeNode root=pRoot;
Queue<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size= queue.size();
ArrayList<Integer> list1=new ArrayList<>();
while (size>0){
root=queue.poll();
list1.add(root.val);
if (root.left!=null){
queue.offer(root.left);
}
if(root.right!=null){
queue.offer(root.right);
}
size--;
}
list.add(list1);
}
return list;
}
}
Nearest common ancestor of binary tree
Nearest common ancestor of binary tree
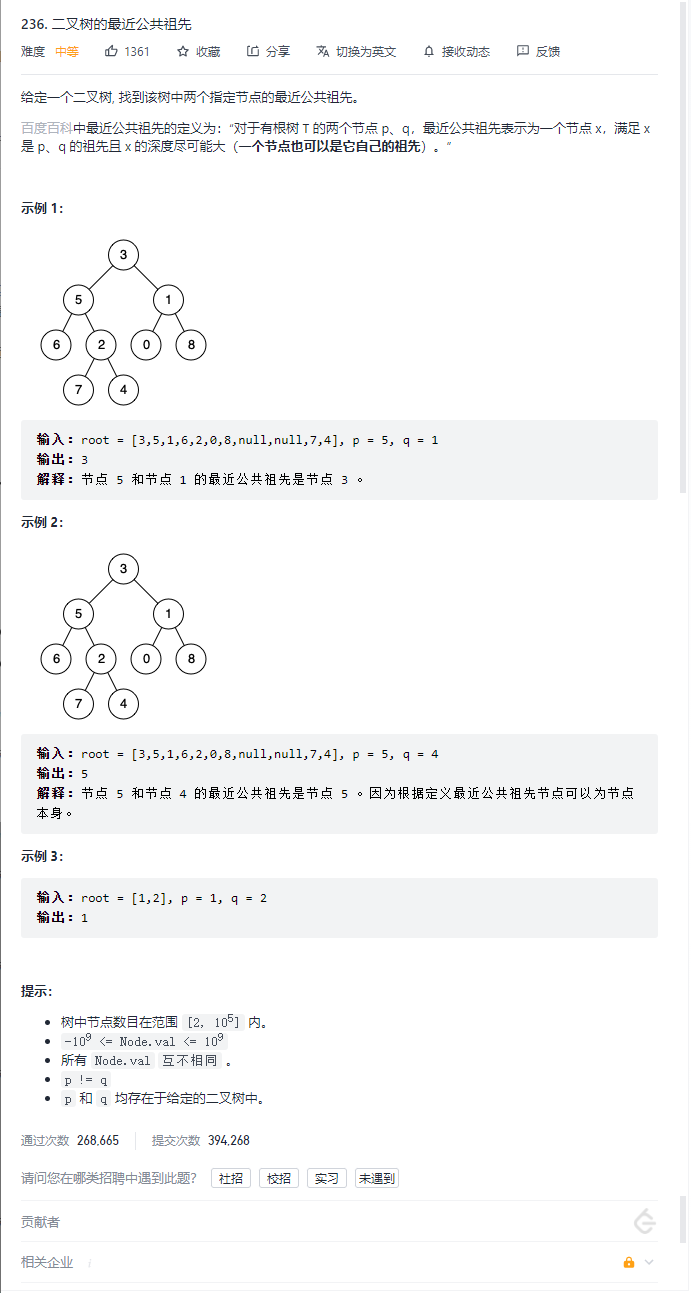
Problem solving idea: first judge whether the root node is empty, then judge whether the root node is equal to p or q, then recurse the left and right subtrees, and finally judge whether the left and right numbers are empty. If they are not empty, return to root. If only one is not empty, return to the node, otherwise return to empty.
The code is as follows:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null){
return null;
}
if(root==p||root==q){
return root;
}
TreeNode leftTree=lowestCommonAncestor(root.left,p,q);
TreeNode rightTree=lowestCommonAncestor(root.right,p,q);
if(leftTree!=null&&rightTree!=null){
return root;
}
if(leftTree==null&&rightTree!=null){
return rightTree;
}
if(leftTree!=null&&rightTree==null){
return leftTree;
}
return null;
}
}
Create a string from a binary tree
Create a string from a binary tree
Solution: this question mainly examines the implementation of preorder traversal, but it should also pay attention to the addition of parentheses. When the left child is empty and the right child is not empty, add a pair of parentheses. If the right child is empty and the left child is not empty, ignore this pair of parentheses.
The code is as follows:
class Solution {
public void tree2strChild(TreeNode t,StringBuilder sb){
if(t==null){
return;
}
sb.append(t.val);
if(t.left==null){
if(t.right!=null){
sb.append("()");
}
else{
return;
}
}
else if(t.left!=null){
sb.append("(");
tree2strChild(t.left,sb);
sb.append(")");
}
if(t.right==null){
return;
}
else{
sb.append("(");
tree2strChild(t.right,sb);
sb.append(")");
}
}
public String tree2str(TreeNode root) {
if(root==null){
return null;
}
StringBuilder sb=new StringBuilder();
tree2strChild(root,sb);
return sb.toString();
}
}
summary
Almost 90% of the above tree questions are completed by recursion, which needs to test our thinking.
Here are some interview questions, hoping to help you
Constructing binary tree from preorder and inorder traversal sequences
Binary search tree and bidirectional linked list
