Chapter 7 sorting algorithm

1. Introduction to sorting algorithm

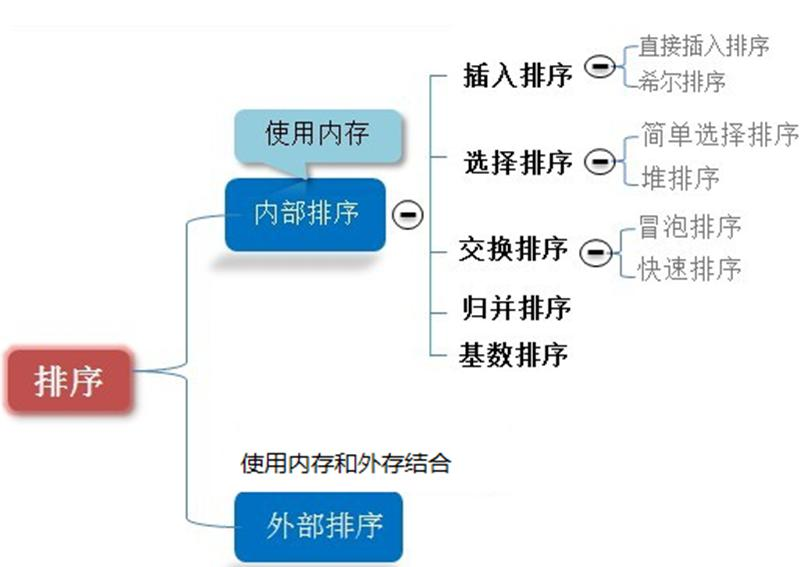
1.1 introduction to sorting algorithm

• Sorting is also called sort algorithm. Sorting is the process of arranging a group of data in a specified order.

1.2 classification of sorting algorithms

• Internal sorting: refers to loading all data to be processed into internal memory (memory) for sorting.
• External sorting method: the amount of data is too large to be loaded into memory. It needs to be sorted with the help of external storage (files, etc.).
• Classification of common sorting algorithms

2. Complexity of algorithm

2.1 measurement method of time complexity

• Post statistical method: this method is feasible, but there are two problems:
  • First, to evaluate the performance of the designed algorithm, we need to actually run the program;
  • Second, the statistics of the obtained time depend on the computer hardware, software and other environmental factors. In this way, it is necessary to run in the same state of the same computer in order to compare which algorithm is faster.
• Ex ante estimation method: determine which algorithm is better by analyzing the time complexity of an algorithm

2.2 time and frequency

• Basic introduction time frequency: the time spent by an algorithm is directly proportional to the execution times of statements in the algorithm. Whichever algorithm has more execution times of statements, it takes more time. The number of statements executed in an algorithm is called statement frequency or time frequency. Denoted as T(n). [example]
• Example - basic case: for example, to calculate the sum of all numbers 1-100, we design two algorithms:

• Example - ignore constant terms:
  • 2n+20 and 2n as n becomes larger, the execution curve is infinitely close, and 20 can be ignored
  • 3n+10 and 3n as n becomes larger, the execution curve is infinitely close, and 10 can be ignored

• Example - ignore lower order items:
  • 2n^2+3n+10 and 2n^2 as n becomes larger, the execution curve is infinitely close, and 3n+10 can be ignored
  • As n^2+5n+20 and n^2 become larger, the execution curve is infinitely close, and 5n+20 can be ignored

• Example - ignore factor:
  • As the value of n increases, 5n^2+7n and 3n^2 + 2n, the execution curves coincide, indicating that 5 and 3 can be ignored in this case.
  • n^3+5n and 6n^3+4n perform curve separation, indicating how many times the method is key

2.3 time complexity

• In general, the number of repeated executions of the basic operation statement in the algorithm is a function of the problem scale n, expressed by T(n). If there is an auxiliary function f(n), so that when n approaches infinity, the limit value of T(n) / f(n) is a constant that is not equal to zero, then f(n) is T(n)
  Function of the same order of magnitude. It is recorded as T(n) = O (f(n)), and O (f(n)) is the asymptotic time complexity of the algorithm, which is called time complexity for short.
• T(n) is different, but the time complexity may be the same. For example: T(n)=n ²+ 7n+6 and T(n)=3n ²+ 2n+2 their T(n) is different, but their time complexity is the same, which is O(n) ²).
• Method for calculating time complexity:
  • Replace all addition constants t (n) = n in the running time with constant 1 ²+ 7n+6 => T(n)=n ²+ 7n+1
  • In the modified run times function, only the highest order term T(n)=n is retained ²+ 7n+1 => T(n)=n ²
  • Coefficient T (n) = n for removing the highest order term ² => T(n) = n ² => O(n ²)

2.4 common time complexity

2.4.1 overview of common time complexity

• Common time complexity
  • Constant order O(1)
  • Logarithmic order O(log2n)
  • Linear order O(n)
  • Linear logarithmic order O(nlog2n)
  • Square order O(n^2)
  • Cubic order O(n^3)
  • K-th order O(n^k)
  • Exponential order O(2^n)
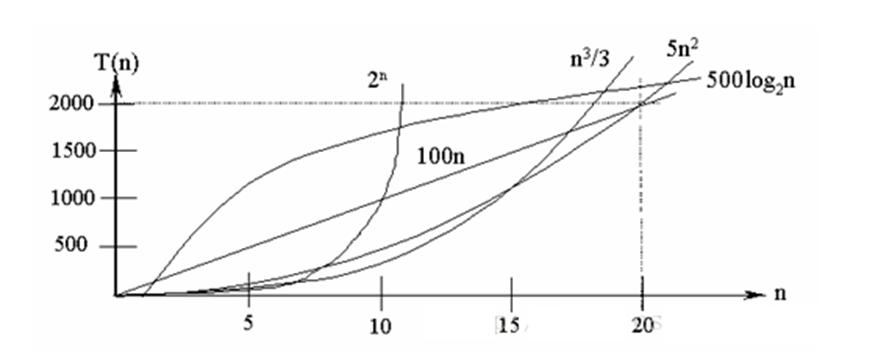
• Conclusion:
  • The time complexity of common algorithms from small to large is as follows: Ο (1)＜ Ο (log2n)＜ Ο (n)＜ Ο (nlog2n)＜ Ο (n2)＜ Ο (n3)＜ Ο (nk) ＜ Ο (2n). As the problem scale n increases, the above time complexity increases,
    The lower the execution efficiency of the algorithm
  • As can be seen from the figure, we should avoid using exponential order algorithm as much as possible

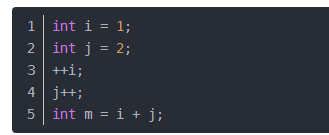
2.4.2 constant order O(1)

• No matter how many lines of code are executed, as long as there is no complex structure such as loop, the time complexity of the code is O(1)
• When the code is executed, its consumption does not increase with the growth of a variable, so no matter how long this kind of code is, even if there are tens of thousands of lines, its time complexity can be expressed by O(1).

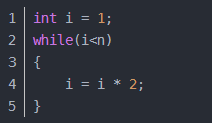
2.4.3 logarithmic order O(log2n)

2.4.4 linear order O(n)

• Note: in this code, the code in the for loop will be executed n times, so its time consumption changes with the change of N, so this kind of code can use O(n) to express its time complexity

2.4.5 linear logarithmic order O(nlogN)

• Note: linear logarithmic order O(nlogN) is actually very easy to understand. If the code with time complexity of O(logn) is cycled N times, its time complexity is n * O(logN), that is, O(nlogN)

2.4.6 square order O(n) ²)

• Description: square order O(n) ²) It is easier to understand that if the code of O(n) is nested and looped again, its time complexity is O(n) ²)， This code is actually nested with two layers of N loops, and its time complexity is O(nn), that is, O(n) ²)
  If n of one layer of loop is changed to m, its time complexity becomes O(mn)

2.4.7 other orders

• Cubic order O(n) ³), K-th order O(n^k)
• Note: refer to O(n) above ²) Just understand, O(n ³) It is equivalent to three-layer N cycle, and others are similar

2.5 average and worst time complexity

• Average time complexity refers to the running time of the algorithm when all possible input instances occur with equal probability.
• The worst-case time complexity is called the worst-case time complexity. The time complexity generally discussed is the worst-case time complexity. The reason for this is that the worst-case time complexity is the limit of the running time of the algorithm on any input instance, which ensures that the running time of the algorithm will not be longer than that in the worst-case.
• Whether the average time complexity is consistent with the worst time complexity is related to the algorithm (as shown in the figure).

2.6 spatial complexity of algorithm

• Similar to the discussion of time complexity, the space complexity of an algorithm is defined as the storage space consumed by the algorithm, which is also a function of the problem scale n.
• Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation. The number of temporary work units occupied by some algorithms is related to the problem-solving scale n. it increases with the increase of N. when n is large, it will occupy more storage units,
  For example, quick sort and merge sort algorithms, cardinal sort is the case
• When doing algorithm analysis, the time complexity is mainly discussed. From the perspective of user experience, we pay more attention to the speed of program execution. Some cache products (redis, memcache) and algorithms (cardinality sorting) essentially trade space for time

3. Bubble sorting

3.1 basic introduction

• The basic idea of Bubble Sorting is to compare the values of adjacent elements from front to back (starting from the elements with smaller subscripts) through the sequence to be sorted, and exchange if the reverse order is found, so that the elements with larger values gradually move from front to back, just like bubbles under the water.
• Optimization: during the sorting process, each element is close to its own position. If there is no exchange after a comparison, it indicates that the sequence is orderly. Therefore, a flag flag should be set during the sorting process to judge whether the elements have been exchanged. This reduces unnecessary comparisons. (optimization here,
  (it can be done after bubble sorting is written)

3.2 bubble sorting diagram

• First trip:

  • Start with the first element of array arr and compare the size with the following element
  • If arr [i] > arr [i + 1], swap and replace the large elements later
  • Since the size of the current element is compared with the following element, you only need to execute the arr.length - 1 loop

• Second trip:

  • Start with the first element of array arr and compare the size with the following element
  • Since the first sorting is completed and the last element of the array is the largest element, you only need to execute the arr.length - 1 - 1 loop

• When will it be finished? Either of the following two conditions can be met:

  • When there is no element exchange position in one sort, it indicates that the array has been ordered

  • Or: follow the above process to finish the second race

    arr.length - 1

    After the trip

    • Think like this: an array of five elements only needs to run four times at most
    • Why only need to run four times at most? Because after four runs, the second element of the array has become the second smallest element of the array, so the array is naturally an ordered array
    • That is, if the array length is n, you need to run n - 1 times

• Summary: two layer for loop

  • The first layer of for loop controls how many times to go: for (int i = 0; I < arr.length - 1; I + +){
  • The second layer of for loop implementation bubbles for this loop: for (int j = 0; J < arr.length - 1 - I; j + +){

• Pseudo code:

for (int i = 0; i < ; i++) {
    for (int j = 0; j < arr.length - 1 - i; j++) {
        // Perform bubbling operation
    }
    if(/* There is no exchange on this trip */) {
        // The array is already in order. Jump out of the loop
    }
}

3.3 code implementation

3.3.1 understand bubble sorting

• The above example is not good. We change the array to: int arr [] = {3, 9, - 1, 10, - 2}, which can better illustrate the characteristics of bubble sorting

public static void main(String[] args) {
	int arr[] = { 3, 9, -1, 10, -2 };
	int temp;

	// In order to understand the capacity, we show you the evolution process of bubble sorting
	System.out.println("Before sorting");
	System.out.println(Arrays.toString(arr));

	// The first sorting is to rank the largest number first from the bottom
	for (int j = 0; j < arr.length - 1; j++) {
		// If the preceding number is larger than the following number, swap
		if (arr[j] > arr[j + 1]) {
			temp = arr[j];
			arr[j] = arr[j + 1];
			arr[j + 1] = temp;
		}
	}
	System.out.println("Array after the first sorting");
	System.out.println(Arrays.toString(arr));

	// The second sorting is to rank the second largest number in the penultimate place
	for (int j = 0; j < arr.length - 1 - 1; j++) {
		// If the preceding number is larger than the following number, swap
		if (arr[j] > arr[j + 1]) {
			temp = arr[j];
			arr[j] = arr[j + 1];
			arr[j + 1] = temp;
		}
	}
	System.out.println("Array after the second sorting");
	System.out.println(Arrays.toString(arr));

	// The third sort is to rank the third largest number in the penultimate place
	for (int j = 0; j < arr.length - 1 - 2; j++) {
		// If the preceding number is larger than the following number, swap
		if (arr[j] > arr[j + 1]) {
			temp = arr[j];
			arr[j] = arr[j + 1];
			arr[j + 1] = temp;
		}
	}
	System.out.println("Array after the third sorting");
	System.out.println(Arrays.toString(arr));

	// The fourth sorting is to rank the fourth largest number in the penultimate position
	for (int j = 0; j < arr.length - 1 - 3; j++) {
		// If the preceding number is larger than the following number, swap
		if (arr[j] > arr[j + 1]) {
			temp = arr[j];
			arr[j] = arr[j + 1];
			arr[j + 1] = temp;
		}
	}
	System.out.println("Array after the fourth sorting");
	System.out.println(Arrays.toString(arr));
}

• Program running results

Before sorting
[3, 9, -1, 10, -2]
Array after the first sorting
[3, -1, 9, -2, 10]
Array after the second sorting
[-1, 3, -2, 9, 10]
Array after the third sorting
[-1, -2, 3, 9, 10]
Array after the fourth sorting
[-2, -1, 3, 9, 10]

3.3.2 write bubble sort

• Test extreme cases

public static void main(String[] args) {
	int arr[] = { 1, 2, 3, 4, 5, 6 };

	// In order to understand the capacity, we show you the evolution process of bubble sorting
	System.out.println("Before sorting");
	System.out.println(Arrays.toString(arr));

	bubbleSort(arr);
}

// The previous bubble sorting algorithm is encapsulated into a method
public static void bubbleSort(int[] arr) {
	// Bubble sort time complexity O(n^2), write it yourself
	int temp = 0; // Temporary variable
	boolean flag = false; // Identification variable, indicating whether exchange has been performed
	for (int i = 0; i < arr.length - 1; i++) {
		for (int j = 0; j < arr.length - 1 - i; j++) {
			// If the preceding number is larger than the following number, swap
			if (arr[j] > arr[j + 1]) {
				flag = true;
				temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
		}
		System.out.println("The first" + (i + 1) + "Sorted array");
		System.out.println(Arrays.toString(arr));
		if (!flag) { // In one sort, no exchange has occurred
			break;
		} else {
			flag = false; // Reset the flag!!! To judge next time
		}
	}
}

• Program running results

Before sorting
[1, 2, 3, 4, 5, 6]
Array after the first sorting
[1, 2, 3, 4, 5, 6]

3.3.3 test bubble sorting performance

• Test code

public static void main(String[] args) {

	// Test the bubble sorting speed O(n^2), give 80000 data, test
	// Create a random array to give 80000
	int[] arr = new int[80000];
	for (int i = 0; i < 80000; i++) {
		arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
	}

	Date date1 = new Date();
	SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
	String date1Str = simpleDateFormat.format(date1);
	System.out.println("The time before sorting is=" + date1Str);

	// Test bubble sort
	bubbleSort(arr);

	Date date2 = new Date();
	String date2Str = simpleDateFormat.format(date2);
	System.out.println("The time after sorting is=" + date2Str);

}

// The previous bubble sorting algorithm is encapsulated into a method
public static void bubbleSort(int[] arr) {
	// Bubble sort time complexity O(n^2), write it yourself
	int temp = 0; // Temporary variable
	boolean flag = false; // Identification variable, indicating whether exchange has been performed
	for (int i = 0; i < arr.length - 1; i++) {

		for (int j = 0; j < arr.length - 1 - i; j++) {
			// If the preceding number is larger than the following number, swap
			if (arr[j] > arr[j + 1]) {
				flag = true;
				temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
		}
		if (!flag) { // In one sort, no exchange has occurred
			break;
		} else {
			flag = false; // Reset the flag!!! To judge next time
		}
	}
}

• Program running results

The time before sorting is=2020-07-15 11:44:08
 The time after sorting is=2020-07-15 11:44:16

4. Select sort

4.1 basic introduction to selection and sorting

• Selective sorting also belongs to the internal sorting method. It is to select an element from the data to be sorted according to the specified rules, and then exchange positions according to the regulations to achieve the purpose of sorting.

4.2 selection and sorting idea

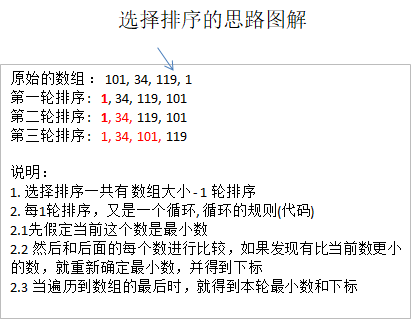
• select sorting is also a simple sorting method. Its basic idea is (n is the size of the array):
  • Select the minimum value from arr[0]~arr[n-1] for the first time and exchange with arr[0]
  • Select the minimum value from arr[1]~arr[n-1] for the second time and exchange with arr[1]
  • Select the minimum value from arr[2]~arr[n-1] for the third time and exchange with arr[2],
  • Select the minimum value from arr[i-1]~arr[n-1] for the ith time, and exchange with arr[i-1],
  • For the nth-1st time, select the minimum value from arr[n-2]~arr[n-1] and exchange it with arr[n-2],
  • Through a total of n-1 times, we get an ordered sequence from small to large according to the sorting code.

4.3. Selection and sorting diagram

• Select sorting process:
  • In the first cycle, the default arr[0] is the smallest element. Compare it with arr[1]~arr[n-1], find the smallest element, and compare it with the position of arr[0]
  • In the second cycle, the default arr[1] is the smallest element. Compare it with arr[2]~arr[n-1], find the smallest element, and compare it with the position of arr[1]
  • In the ith cycle, the default arr[i] is the smallest element. Compare it with arr[i+1]~arr[n-1], find the smallest element, and compare it with the position of arr[i]
  • Until the loop executes n - 1 times
• Summary: two layer for loop
  • The first layer of for loop controls how many times to go: for (int i = 0; I < arr.length - 1; I + +){
    • Start with the first element of the array, because each time you compare the current element arr[j] with the next element arr[j+1]
    • At the end of the penultimate element of the array, after comparing arr[arr.length - 2] with arr[arr.length - 1], the array is already an ordered array
    • If the array size is n, the array will be an ordered array after the n - 1 pass
  • The second layer of for loop controls the selection sorting from the first few elements: for (int j = I + 1; J < arr.length; j + +)
    • Each time you enter the for loop of the second layer, first assume that the current element arr[i] is the smallest element: min = arr[i], And record the subscript of the smallest element: index = i;
    • Then compare with the following element arr[j] in turn. If an element smaller than arr[i] is found, update the index of the minimum value and the minimum value: min = arr[j]; index = j ;

4.4 code implementation

4.4.1 understanding, selecting and sorting

• Step by step understanding the selection sorting algorithm

//Select sort
public class SelectSort {

	public static void main(String[] args) {
        
		int[] arr = { 101, 34, 119, 1 };
		selectSort(arr);
        
	}

	// Select sort
	public static void selectSort(int[] arr) {
        
		// Use step-by-step derivation to explain the selection and sorting
		// Round 1
		// Original array: 101, 34, 119, 1
		// First round sorting: 1, 34, 119, 101
		// The algorithm should be simple first -- to be complex means that a complex algorithm can be divided into simple problems and solved step by step

		// Round 1
		int minIndex = 0;
		int min = arr[0];
		for (int j = 0 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // Indicates the assumed minimum value, not the minimum
				min = arr[j]; // Reset min
				minIndex = j; // Reset minIndex
			}
		}
		// Put the minimum value in arr[0], that is, exchange
		if (minIndex != 0) {
			arr[minIndex] = arr[0];
			arr[0] = min;
		}
		System.out.println("After the 1st round~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 119, 101

		// Round 2
		minIndex = 1;
		min = arr[1];
		for (int j = 1 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // Indicates the assumed minimum value, not the minimum
				min = arr[j]; // Reset min
				minIndex = j; // Reset minIndex
			}
		}
		// Put the minimum value in arr[0], that is, exchange
		if (minIndex != 1) {
			arr[minIndex] = arr[1];
			arr[1] = min;
		}
		System.out.println("After the second round~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 119, 101

		// Round 3
		minIndex = 2;
		min = arr[2];
		for (int j = 2 + 1; j < arr.length; j++) {
			if (min > arr[j]) { // Indicates the assumed minimum value, not the minimum
				min = arr[j]; // Reset min
				minIndex = j; // Reset minIndex
			}
		}
		// Put the minimum value in arr[0], that is, exchange
		if (minIndex != 2) {
			arr[minIndex] = arr[2];
			arr[2] = min;
		}
		System.out.println("After the 3rd round~~");
		System.out.println(Arrays.toString(arr));// 1, 34, 101, 119
	}

}

• Program running results

After the 1st round~~
[1, 34, 119, 101]
After the second round~~
[1, 34, 119, 101]
After the 3rd round~~
[1, 34, 101, 119]

4.4.2. Compilation, selection and sorting

• Write selection sorting algorithm

//Select sort
public class SelectSort {

	public static void main(String[] args) {
		int[] arr = { 101, 34, 119, 1 };
		selectSort(arr);
	}

	// Select sort
	public static void selectSort(int[] arr) {

		// In the process of derivation, we found the law, so we can use for to solve it
		// The selection sorting time complexity is O(n^2)
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			int min = arr[i];
			for (int j = i + 1; j < arr.length; j++) {
				if (min > arr[j]) { // Indicates the assumed minimum value, not the minimum
					min = arr[j]; // Reset min
					minIndex = j; // Reset minIndex
				}
			}

			// Put the minimum value in arr[0], that is, exchange
			if (minIndex != i) {
				arr[minIndex] = arr[i];
				arr[i] = min;
			}

			System.out.println("The first" + (i + 1) + "After wheel~~");
			System.out.println(Arrays.toString(arr));
		}

	}
}

• Program running results

After the 1st round~~
[1, 34, 119, 101]
After the second round~~
[1, 34, 119, 101]
After the 3rd round~~
[1, 34, 101, 119]

4.4.3 test selection and sorting performance

• Test code

//Select sort
public class SelectSort {

	public static void main(String[] args) {

		//Create a random array to give 80000
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
		}
		
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("The time before sorting is=" + date1Str);

		selectSort(arr);

		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("The time before sorting is=" + date2Str);

	}

	// Select sort
	public static void selectSort(int[] arr) {

		// In the process of derivation, we found the law, so we can use for to solve it
		// The selection sorting time complexity is O(n^2)
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			int min = arr[i];
			for (int j = i + 1; j < arr.length; j++) {
				if (min > arr[j]) { // Indicates the assumed minimum value, not the minimum
					min = arr[j]; // Reset min
					minIndex = j; // Reset minIndex
				}
			}

			// Put the minimum value in arr[0], that is, exchange
			if (minIndex != i) {
				arr[minIndex] = arr[i];
				arr[i] = min;
			}
		}

	}
}

• Program running results

The time before sorting is=2020-07-15 19:59:19
 The time before sorting is=2020-07-15 19:59:20

4.5 summary

• Since the selection sorting algorithm only needs to record the minimum value and the index of the minimum value in the array after meeting the if (min > arr [J]) {condition in the innermost for loop, and there is no need to perform the exchange operation every time like bubble sorting, the execution speed of the selection sorting algorithm is faster than that of bubble sorting algorithm

5. Insert sort

5.1 basic introduction to insertion sorting

• Plug in sorting belongs to internal sorting method, which is to find the appropriate position of the element to be sorted by inserting, so as to achieve the purpose of sorting.

5.2. Insert sorting idea

• The basic idea of Insertion Sorting is to treat n elements to be sorted as an ordered table and an unordered table
• At the beginning, the ordered table contains only one element, and the unordered table contains n-1 elements. In the sorting process, take the first element from the unordered table every time, compare its sorting code with the sorting code of the ordered table elements in turn, and insert it into the appropriate position in the ordered table to make it a new ordered table

5.3. Insert sorting diagram

• Insert sort logic:

  • Firstly, the array is divided into two arrays. The first part is an ordered array and the second part is an unordered array. Our purpose is to take out the values in the unordered array bit by bit and put them in the area of the ordered array
  • First pass: arr[0] is the element of the ordered array, and arr[1] is the first element in the unordered array. Compare arr[1] with arr[0], and the goal is to insert arr[1] into the ordered array
  • First pass: arr[0] and arr[1] are the elements of the ordered array, and arr[2] is the first element in the unordered array. Compare arr[2] with arr[0] and arr[1], and the goal is to insert arr[2] into the ordered array
  • Trip I: arr[0]~arr[i] is the element of the ordered array, and arr[i+1] is the first element in the unordered array. Compare arr[i+1] with arr[0]~arr[i]. The goal is to insert arr[i+1] into the ordered array
  • Trip n-1: at this time, the ordered array is arr[0]~arr[n-2], and the unordered array is arr[n-1]. Insert the last element in the unordered array into the ordered array
  • How to insert?
    • Suppose there is a pointer (index) pointing to the first element in the unordered array, that is, arr[index] is the first element in the unordered array. We define a variable to store the value: int insertVal = arr[index]
      ;, now insert it into the previous ordered array
    • Move the index one step forward to point to the last element of the ordered array. We define a new variable to store the pointer: insertIndex = index - 1;, that is, arr[insertIndex] is the last element of the ordered array
    • We need to find a value smaller than insertVal and insert insertVal after the value:
      • If insertval > arr [insertindex], perform the insertion
      • If insertval < arr [insertIndex], move the ordered array backward to make room for insertion, move the insertIndex pointer forward, and then check whether the previous element meets the conditions until the insertion position is found
      • That is, the cycle termination condition is to find the insertion position, which can be divided into two cases:
        • Find the insertion position in the middle of the ordered array
        • insertVal is smaller than all the numbers in the ordered array and is inserted in the first position of the array (in the case of insertIndex = 0)

• Summary: two-layer cycle

  • The for loop controls how many times to go: for (int i = 1; I < arr.length; I + +) {, starting from the first element of the array and ending at the last element of the array

  • The while loop continuously moves the pointer forward, finds the insertion position in the ordered array, and executes the insertion:

    while (insertIndex >= 0 && insertVal < arr[insertIndex]) {

5.4 code implementation

5.4.1 understand insertion sorting

• Understand insertion sorting algorithm

public class InsertSort {

	public static void main(String[] args) {
        
		int[] arr = { 101, 34, 119, 1 };
		insertSort(arr);

	}

	// Insert sort
	public static void insertSort(int[] arr) {

		// Use step-by-step derivation to explain and facilitate understanding
		// Round 1 {101, 34, 119, 1}; = > {34, 101, 119, 1}

		// {101, 34, 119, 1}; => {101,101,119,1}
		// Defines the number of to insert
		int insertVal = arr[1];
		int insertIndex = 1 - 1; // That is, the subscript of the number before arr[1]

		// Find the insertion position for insertVal
		// explain
		// 1. Insertindex > = 0 ensure that the insertion position of insertVal is not exceeded
		// 2. Insertval < arr [insertindex] the number to be inserted, and the insertion position has not been found
		// 3. You need to move arr[insertIndex] backward
		while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
			arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
			insertIndex--;
		}
		// When exiting the while loop, the insertion position is found, insertIndex + 1
		// Example: I can't understand. Let's debug later
		arr[insertIndex + 1] = insertVal;

		System.out.println("Round 1 insertion");
		System.out.println(Arrays.toString(arr));

		// Round 2
		insertVal = arr[2];
		insertIndex = 2 - 1;

		while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
			arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
			insertIndex--;
		}

		arr[insertIndex + 1] = insertVal;
		System.out.println("Round 2 insertion");
		System.out.println(Arrays.toString(arr));

		// Round 3
		insertVal = arr[3];
		insertIndex = 3 - 1;

		while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
			arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
			insertIndex--;
		}

		arr[insertIndex + 1] = insertVal;
		System.out.println("Round 3 insertion");
		System.out.println(Arrays.toString(arr));

	}

}

• Program running results

Round 1 insertion
[34, 101, 119, 1]
Round 2 insertion
[34, 101, 119, 1]
Round 3 insertion
[1, 34, 101, 119]

5.4.2. Write insert sort

• Write insertion sorting algorithm

public class InsertSort {

	public static void main(String[] args) {
        
		int[] arr = { 101, 34, 119, 1 };
		insertSort(arr);

	}

	// Insert sort
	public static void insertSort(int[] arr) {
		int insertVal = 0;
		int insertIndex = 0;
		//Use the for loop to simplify the code
		for(int i = 1; i < arr.length; i++) {
			//Defines the number of to insert
			insertVal = arr[i];
			insertIndex = i - 1; // That is, the subscript of the number before arr[1]
	
			// Find the insertion position for insertVal
			// explain
			// 1. Insertindex > = 0 ensure that the insertion position of insertVal is not exceeded
			// 2. Insertval < arr [insertindex] the number to be inserted, and the insertion position has not been found
			// 3. You need to move arr[insertIndex] backward
			while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
				arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
				insertIndex--;
			}
			// When exiting the while loop, the insertion position is found, insertIndex + 1
			// Because the value of the element we found, that is, the element with the subscript insertIndex, is smaller than insertVal
             // So we want to insert insertVal into insertIndex + 1
			arr[insertIndex + 1] = insertVal;
			System.out.println("The first"+i+"Wheel insertion");
			System.out.println(Arrays.toString(arr));
		}

	}

}

• Program running results

Round 1 insertion
[34, 101, 119, 1]
Round 2 insertion
[34, 101, 119, 1]
Round 3 insertion
[1, 34, 101, 119]

5.4.3 test insertion sorting performance

• Test insert sort performance

public class InsertSort {

	public static void main(String[] args) {
		
		// Create a random array to give 80000
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
		}

		System.out.println("Before inserting sort");
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("The time before sorting is=" + date1Str);

		insertSort(arr); // Call insert sort algorithm

		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("The time before sorting is=" + date2Str);

	}

	// Insert sort
	public static void insertSort(int[] arr) {
		int insertVal = 0;
		int insertIndex = 0;
		//Use the for loop to simplify the code
		for(int i = 1; i < arr.length; i++) {
			//Defines the number of to insert
			insertVal = arr[i];
			insertIndex = i - 1; // That is, the subscript of the number before arr[1]
	
			// Find the insertion position for insertVal
			// explain
			// 1. Insertindex > = 0 ensure that the insertion position of insertVal is not exceeded
			// 2. Insertval < arr [insertindex] the number to be inserted, and the insertion position has not been found
			// 3. You need to move arr[insertIndex] backward
			while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
				arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
				insertIndex--;
			}
			// When exiting the while loop, the insertion position is found, insertIndex + 1
			// Example: I can't understand. Let's debug later
			//Here we judge whether assignment is required
			arr[insertIndex + 1] = insertVal;
		}

	}

}

• Program running results

Before inserting sort
 The time before sorting is=2020-07-15 21:49:48
 The time before sorting is=2020-07-15 21:49:50

5.5 summary

• When finding the insertion position, insertion sort needs to move the array elements as a whole, so the efficiency is slightly lower than selection sort

6. Hill sort

6.1. Simple insertion sorting problem

• Let's look at the possible problems of simple insertion sorting. Array arr = {2, 3, 4, 5, 6, 1} the number of inserts to be inserted is 1 (minimum). The process of simple insertion sorting is as follows
• Conclusion: when the number of inserts is small, the number of backward moves increases significantly, which has an impact on the efficiency

{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}

6.2 basic introduction to Hill sorting

• Hill sort is a sort algorithm proposed by Donald Shell in 1959. Hill sort is also an insertion sort. It is a more efficient version of simple insertion sort, also known as reduced incremental sort.

6.3. Basic idea of Hill ranking

• Hill sort groups the arrays according to the increment, and uses the direct insertion sorting algorithm for each group; with the increment decreasing, each group contains more and more keywords. When the increment is reduced to 1, the whole file is divided into one group, and the algorithm terminates

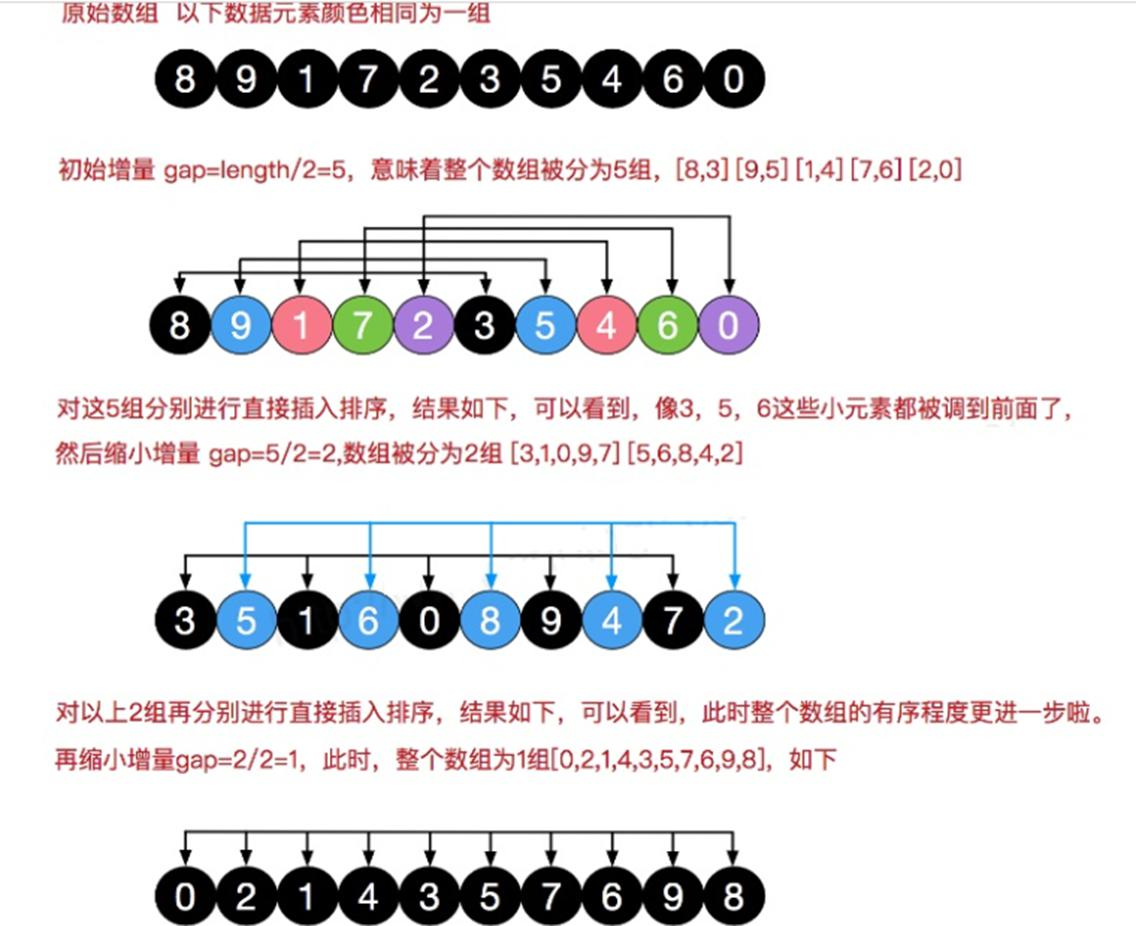
6.4 Hill ranking diagram (exchange method)

• The first time: gap = arr.length/5 = 5, the array is divided into five groups, and the index difference of each array element is 5

  • How to complete the first sorting?
    • Think about it, we need a loop to sort the elements in each group
    • There are five groups in total. We need another cycle
    • Therefore, two layers of loops are required to complete each sorting
  • The program code is as follows. i and j are regarded as auxiliary pointers:
    • i and j are used together to move the pointer from the first element of the array to the last element. The purpose is to traverse the array
    • j and i are used together to traverse forward from the array index i every time, move gap positions forward every time, and then exchange (bubble sorting): see if the previous element is greater than my value. If the previous element is greater than my value, i will exchange positions with him and run to the front

  // Round 1 of Hill sort
  // Because the first round of sorting is to divide 10 data into 5 groups
  for (int i = 5; i < arr.length; i++) {
      // Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
      for (int j = i - 5; j >= 0; j -= 5) {
          // If the current element is larger than the element after adding the step size, it indicates the exchange
          if (arr[j] > arr[j + 5]) {
              temp = arr[j];
              arr[j] = arr[j + 5];
              arr[j + 5] = temp;
          }
      }
  }
  
  

• The second time: gap = gap /2 = 2;, divide the array into two groups, and the index of each array element differs by 2

  • Group 1:
    • When i = 2, the array traverses forward from index 2 at an interval of 2: sort arr[0] and arr[2]
    • When i = 4, the array traverses forward from index 4 at an interval of 2: sort arr[0], arr[2], and arr[4]
    • When i = 6, the array traverses forward from index 6 with an interval of 2: sort arr[0], arr[2], arr[4] and arr[6]
    • When i = 8, the array traverses forward from index 8 with an interval of 2: sort arr[0], arr[2], arr[4], arr[6] and arr[8]
  • Group 2:
    • When i = 3, the array traverses forward from index 3 at an interval of 2: sort arr[1] and arr[3]
    • When i = 5, the array traverses forward from index 5 with an interval of 2: sort arr[1], arr[3], and arr[5]
    • When i = 7, the array traverses forward from index 7 at an interval of 2: sort arr[1], arr[3], arr[5] and arr[7]
    • When i = 9, the array traverses forward from index 9 with an interval of 2: sort arr[1], arr[3], arr[5], arr[7], and arr[9]

// Round 2 of Hill sort
// Because the second round of sorting is to divide 10 data into 5 / 2 = 2 groups
for (int i = 2; i < arr.length; i++) {
    // Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
    for (int j = i - 2; j >= 0; j -= 2) {
        // If the current element is larger than the element after adding the step size, it indicates the exchange
        if (arr[j] > arr[j + 2]) {
            temp = arr[j];
            arr[j] = arr[j + 2];
            arr[j + 2] = temp;
        }
    }
}
System.out.println("Hill sort after 2 rounds=" + Arrays.toString(arr));

• third time:

  gap = gap /2 = 1;

  , the array is divided into a group, and the index difference of each array element is 1. For the exchange method, this is abnormal bubble sorting

  • When i = 1, the array traverses forward from index 1 at an interval of 1: sort arr[0] and arr[1]
  • When i = 2, the array traverses forward from index 2 at an interval of 1: sort arr[0], arr[1], and arr[2]
  • When i = 3, the array traverses forward from index 3 with an interval of 1: sort arr[0], arr[1], arr[2], and arr[3]
  • ...

// Round 3 of Hill sort
// Because the third round of sorting is to divide 10 data into 2 / 2 = 1 groups
for (int i = 1; i < arr.length; i++) {
    // Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
    for (int j = i - 1; j >= 0; j -= 1) {
        // If the current element is larger than the element after adding the step size, it indicates the exchange
        if (arr[j] > arr[j + 1]) {
            temp = arr[j];
            arr[j] = arr[j + 1];
            arr[j + 1] = temp;
        }
    }
}
System.out.println("Hill sort after 3 rounds=" + Arrays.toString(arr));

• Summary: change the value of gap every time using the loop (initial value: array size / 2, then: gap = gap/2), and then nest the above double-layer for loop in the loop changing gap

  • Change gap: for (int gap = arr.length/2; gap > 0; gap / = 2){
  • Inner loop: sort each group of arrays

  for (int i = gap; i < arr.length; i++) {
      // Traverse all elements in each group (a total of gap groups, with? Elements in each group), step gap
      for (int j = i - gap; j >= 0; j -= gap) {
      }
  }
  

    
- Hill sort pseudo code
    
    ```java
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < arr.length; i++) {
        	// Traverse all elements in each group (a total of gap groups, with? Elements in each group), step gap
        	for (int j = i - gap; j >= 0; j -= gap) {
                // Bubble sort each group
            }
        }
    }
    

6.5 code implementation

6.5.1 understanding Hill sorting (exchange method)

• Understand Hill sort based on exchange method

public class ShellSort {

	public static void main(String[] args) {
        
		int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
		shellSort(arr);

	}

	// Use step-by-step derivation to write Hill sort
	// In Hill sorting, the exchange method is adopted for the insertion of ordered sequences,
	// Idea (algorithm) = = > code
	public static void shellSort(int[] arr) {

		int temp = 0;

		// Round 1 of Hill sort
		// Because the first round of sorting is to divide 10 data into 5 groups
		for (int i = 5; i < arr.length; i++) {
			// Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
			for (int j = i - 5; j >= 0; j -= 5) {
				// If the current element is larger than the element after adding the step size, it indicates the exchange
				if (arr[j] > arr[j + 5]) {
					temp = arr[j];
					arr[j] = arr[j + 5];
					arr[j + 5] = temp;
				}
			}
		}
		System.out.println("Hill sort after 1 round=" + Arrays.toString(arr));

		// Round 2 of Hill sort
		// Because the second round of sorting is to divide 10 data into 5 / 2 = 2 groups
		for (int i = 2; i < arr.length; i++) {
			// Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
			for (int j = i - 2; j >= 0; j -= 2) {
				// If the current element is larger than the element after adding the step size, it indicates the exchange
				if (arr[j] > arr[j + 2]) {
					temp = arr[j];
					arr[j] = arr[j + 2];
					arr[j + 2] = temp;
				}
			}
		}
		System.out.println("Hill sort after 2 rounds=" + Arrays.toString(arr));

		// Round 3 of Hill sort
		// Because the third round of sorting is to divide 10 data into 2 / 2 = 1 groups
		for (int i = 1; i < arr.length; i++) {
			// Traverse all elements in each group (5 groups in total, 2 elements in each group) in steps of 5
			for (int j = i - 1; j >= 0; j -= 1) {
				// If the current element is larger than the element after adding the step size, it indicates the exchange
				if (arr[j] > arr[j + 1]) {
					temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
			}
		}
		System.out.println("Hill sort after 3 rounds=" + Arrays.toString(arr));

	}
}

• Program running results

Hill sort after 1 round=[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]
Hill sort after 2 rounds=[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
Hill sort after 3 rounds=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

6.5.2 compiling Hill sort (exchange method)

• Write Hill sorting algorithm based on exchange method

public class ShellSort {

	public static void main(String[] args) {

		int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
		shellSort(arr);

	}

	// Use step-by-step derivation to write Hill sort
	// In Hill sorting, the exchange method is adopted for the insertion of ordered sequences,
	// Idea (algorithm) = = > code
	public static void shellSort(int[] arr) {

		int temp = 0;
		int count = 0;
		// Based on the previous step-by-step analysis, cyclic processing is used
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			for (int i = gap; i < arr.length; i++) {
				// Traverse all elements in each group (a total of gap groups, with? Elements in each group), step gap
				for (int j = i - gap; j >= 0; j -= gap) {
					// If the current element is larger than the element after adding the step size, it indicates the exchange
					if (arr[j] > arr[j + gap]) {
						temp = arr[j];
						arr[j] = arr[j + gap];
						arr[j + gap] = temp;
					}
				}
			}
			System.out.println("Hill sort No" + (++count) + "round =" + Arrays.toString(arr));
		}
        
}

• Program running results

Hill sort round 1 =[3, 5, 1, 6, 0, 8, 9, 4, 7, 2]
Hill sort round 2 =[0, 2, 1, 4, 3, 5, 7, 6, 9, 8]
Hill sort round 3 =[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

6.5.3 test Hill sorting (exchange method) performance

• Test the performance of hill sorting algorithm based on exchange method

public class ShellSort {

	public static void main(String[] args) {

		// Create a random array to give 80000
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
		}

		System.out.println("Before sorting");
		Date date1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(date1);
		System.out.println("The time before sorting is=" + date1Str);

		shellSort(arr); // Exchange type

		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("The time before sorting is=" + date2Str);

	}

	// Use step-by-step derivation to write Hill sort
	// In Hill sorting, the exchange method is adopted for the insertion of ordered sequences,
	// Idea (algorithm) = = > code
	public static void shellSort(int[] arr) {

		int temp = 0;
		int count = 0;
		// Based on the previous step-by-step analysis, cyclic processing is used
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			for (int i = gap; i < arr.length; i++) {
				// Traverse all elements in each group (a total of gap groups, with? Elements in each group), step gap
				for (int j = i - gap; j >= 0; j -= gap) {
					// If the current element is larger than the element after adding the step size, it indicates the exchange
					if (arr[j] > arr[j + gap]) {
						temp = arr[j];
						arr[j] = arr[j + gap];
						arr[j + gap] = temp;
					}
				}
			}
		}
	}
    
}

• Program running results

Before sorting
 The time before sorting is=2020-07-16 10:22:27
 The time before sorting is=2020-07-16 10:22:33

• Analysis: because the hill sorting algorithm is implemented by the exchange method, the hill sorting algorithm based on the exchange method is slower than the simple selection sorting algorithm, so we must write the hill sorting algorithm based on the insertion method

6.5.4 compiling Hill sort (insertion method)

• Write Hill sorting algorithm based on insertion method:

  • Record the element value of the current position

    int temp = arr[j]

    , start from the previous position of the current element, look forward, and move gap distances each time

    • If temp < arr [J - gap]:
      • Move the array element backward to make room for insertion: arr[j] = arr[j - gap];
      • Then continue to look forward: j -= gap;
    • If temp > arr [j - gap], find the insertion position and execute the insertion. arr[j] = temp; because the insertion space has been made up in the previous step and the pointer j has been moved forward, it can be inserted directly
    • If the front of the array is found or the insertion position is not found: J - gap < 0, it proves that temp needs to be inserted at the front of the array

  • Just replace the bubbling operation of the previous exchange method with the insertion operation

public class ShellSort {

	public static void main(String[] args) {

		int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };
		
		System.out.println("Before sorting");
		System.out.println(Arrays.toString(arr));
		
		shellSort(arr);
		
		System.out.println("Before sorting");
		System.out.println(Arrays.toString(arr));

	}

	// Optimize Hill sort of commutative - > shift method
	public static void shellSort(int[] arr) {
		// Increment gap, and gradually reduce the increment
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			// From the gap element, directly insert and sort the groups one by one
			for (int i = gap; i < arr.length; i++) {
				int j = i;
				int temp = arr[j];
				if (arr[j] < arr[j - gap]) {
					while (j - gap >= 0 && temp < arr[j - gap]) {
						// move
						arr[j] = arr[j - gap];
						j -= gap;
					}
					// temp is larger than arr[j - gap], so it needs to be inserted at j
					arr[j] = temp;
				}

			}
		}
	}

}

• Program running results

Before sorting
[8, 9, 1, 7, 2, 3, 5, 4, 6, 0]
Before sorting
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

6.5.5 test Hill sorting (insertion method) performance

• Test the performance of hill sorting algorithm based on insertion method

public class ShellSort {

	public static void main(String[] args) {

		// Create a random array to give 80000
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
		}

		System.out.println("Before sorting");
		Date date1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(date1);
		System.out.println("The time before sorting is=" + date1Str);

		shellSort(arr); // Exchange type

		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("The time before sorting is=" + date2Str);

	}

	// Optimize Hill sort of commutative - > shift method
	public static void shellSort(int[] arr) {
		// Increment gap, and gradually reduce the increment
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			// From the gap element, directly insert and sort the groups one by one
			for (int i = gap; i < arr.length; i++) {
				int j = i;
				int temp = arr[j];
				if (arr[j] < arr[j - gap]) {
					while (j - gap >= 0 && temp < arr[j - gap]) {
						// move
						arr[j] = arr[j - gap];
						j -= gap;
					}
					// After exiting while, find the insertion location for temp
					arr[j] = temp;
				}

			}
		}
	}

}

• Program running results: less than 1s, really fast

Before sorting
 The time before sorting is=2020-07-16 11:02:20
 The time before sorting is=2020-07-16 11:02:20

• Test results of eight million data

Before sorting
 The time before sorting is=2020-07-16 14:38:55
 The time before sorting is=2020-07-16 14:38:57

7. Quick sort

7.1 introduction to fast exhaust

1. Quick sort is a sort algorithm developed by Tony hall. On average, sorting n items takes more time Ο (nlogn) comparisons. Required in the worst case Ο (n2) comparisons, but this situation is not common. In fact, quick sorting is usually significantly better than others Ο (nlogn)
   The algorithm is faster because its inner loop can be implemented efficiently on most architectures.
2. Quick sort uses Divide and conquer strategy to divide a serial list into two sub lists.
3. In essence, quick sort should be regarded as a recursive divide and conquer method based on bubble sort.
4. The name of quick sort is simple and rough, because you know the meaning of its existence as soon as you hear the name. It is fast and efficient! It is one of the fastest sorting algorithms to process big data.
5. Although the time complexity of Worst Case reaches O(n ²)， But others are excellent. In most cases, they perform better than the sorting algorithm with an average time complexity of O(n logn), but I don't know why. Fortunately, my obsessive-compulsive disorder has been committed again. I checked N
   Many materials finally found a satisfactory answer in the algorithm art and informatics competition:
6. The worst case for quicksort is O(n) ²)， For example, the fast arrangement of sequential sequence, but its expected spreading time is O(nlogn), and the constant factor implicit in the O(nlogn) sign is very small, and the specific complexity is stable, equal to O(nlogn)
   Therefore, for the vast majority of random number sequences with weak order, quick sort is always better than merge sort.

7.2 code ideas

1. Pick out an element from the sequence and call it "pivot"; individuals like to use the number corresponding to the middle subscript
2. Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side).
3. After the partition exits, the benchmark is in the middle of the sequence. This is called partition operation;
4. Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element;

Analysis of quick discharge process

Quicksort is an improvement on bubble sort. The basic idea is: divide the data to be sorted into two independent parts through one-time sorting, and all the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method**
The whole sorting process can be performed recursively * *, so that the whole data becomes an ordered sequence

7.3 code implementation

7.3.1 write fast scheduling algorithm

• Quick code

private static void quickSort(int[] arr, int left, int right) {
    int l = left; //Left subscript
    int r = right; //Right subscript
    int pivot = arr[(left + right) / 2];
    System.out.println("(left + right) / 2 = " + (left + right) / 2 + " pivot = " + pivot);
    int temp = 0;
    while (l < r) {
        while (arr[l] < pivot) {
            l++;
        }
        while (arr[r] > pivot) {
            r--;
        }
        if (l >= r) {
            break;
        }
        temp = arr[l];
        arr[l] = arr[r];
        arr[r] = temp;

        if (arr[l] == pivot) {
            r--;
        }
        if (arr[r] == pivot) {
            l++;
        }
        System.out.println(Arrays.toString(arr));// 1, 34, 119, 101
    }
    System.out.println("===");
    // If l == r, it must be l++, r --, otherwise stack overflow occurs
    if (l == r) {
        l++;
        r--;
    }

    //Left recursion
    if (left < r) {
        System.out.println("Left recursion");
        quickSort2(arr, left, r);
    }
    //Recursive right
    if (l < right) {
        System.out.println("Recursive right");
        quickSort2(arr, l, right);
    }
}

• Test code

public static void main(String[] args) {
    int[] arr = {4561, -9, 78, 0, 23, -567, 70, -1, 900};
    quickSort(arr, 0, arr.length - 1);
    System.out.println(Arrays.toString(arr));
}

• Program output

arr=[-567, -9, -1, 0, 23, 70, 78, 900, 4561]

7.3.2 test quick sort performance

• Compile and test the performance of quick sorting algorithm

public class QuickSort {

    public static void main(String[] args) {
        //        int[] arr = {4561, -9, 78, 0, 23, -567, 70, -1, 900};

        //        Test the execution speed of fast platoon
        //         Create a random array to give 80000
        int[] arr = new int[800000];
        for (int i = 0; i < 800000; i++) {
            arr[i] = (int) (Math.random() * 80000000); // Generate a [0, 8000000) number
        }

        System.out.println("Before sorting");
        Date data1 = new Date();
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String date1Str = simpleDateFormat.format(data1);
        System.out.println("The time before sorting is=" + date1Str);

        quickSort(arr, 0, arr.length - 1);

        Date data2 = new Date();
        String date2Str = simpleDateFormat.format(data2);
        System.out.println("The time before sorting is=" + date2Str);
        //        System.out.println("arr=" + Arrays.toString(arr));
    }

    public static void quickSort(int[] arr, int left, int right) {
        int l = left; //Left subscript
        int r = right; //Right subscript
        //pivot axis value
        int pivot = arr[(left + right) / 2];
        int temp = 0; //Temporary variable, used in exchange
        //The purpose of the while loop is to put smaller than the pivot value to the left
        //Larger than pivot value to the right
        while (l < r) {
            //Keep looking on the left side of pivot, and exit only after finding a value greater than or equal to pivot
            while (arr[l] < pivot) {
                l += 1;
            }
            //Keep looking on the right side of pivot, and exit only after finding a value less than or equal to pivot
            while (arr[r] > pivot) {
                r -= 1;
            }
            //If l > = R, it indicates that the left and right values of pivot are all on the left
            //Less than or equal to the pivot value, and all on the right are greater than or equal to the pivot value
            if (l >= r) {
                break;
            }

            //exchange
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            //If after the exchange, it is found that this arr[l] == pivot value is equal to r --, move forward
            //After the exchange, arr[l] == pivot indicates that the r subscript has pointed to the location of the pivot before the exchange,
            //r -- is to skip this pivot position
            if (arr[l] == pivot) {
                r -= 1;
            }
            //If after the exchange, it is found that the arr[r] == pivot value is equal to l + +, move it back
            if (arr[r] == pivot) {
                l += 1;
            }
        }

        // If l == r, it must be l++, r --, otherwise stack overflow occurs
        if (l == r) {
            l += 1;
            r -= 1;
        }

        //Left recursion
        if (left < r) {
            quickSort(arr, left, r);
        }
        //Recursive right
        if (right > l) {
            quickSort(arr, l, right);
        }
    }
}

• Program running results: 800000 data a second, really fast.

Before sorting
 The time before sorting is=2021-11-11 16:47:19
 The time before sorting is=2021-11-11 16:47:20

8. Merge sort

8.1 basic introduction to merging and sorting

• Merge sort is a sort method based on the idea of merging. The algorithm adopts the classical divide and conquer strategy
• Divide and conquer divides the problem into some small problems and then solves them recursively, while the conquer stage "fixes" the answers obtained in different stages, that is, divide and conquer

8.2. Merging and sorting idea

• Sub -- > treatment

8.3 thoughts on merging and sorting codes

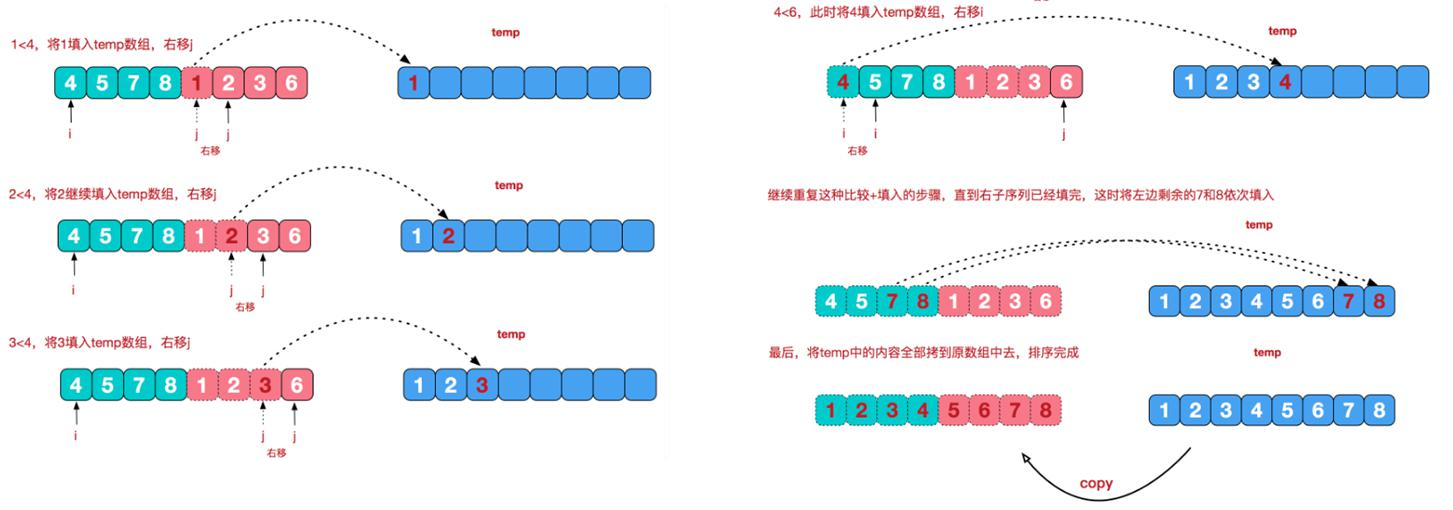
• When merging, you actually merge two adjacent sub arrays (arr1 and arr2) in the original array (ARR)

  , we use three pointers to represent the position of the two subarrays in the original array

  • arr[left] ~ arr[mid] is arr1
  • arr[mid + 1] ~ arr[right] is arr2

• How to merge?

  • First, you need a temporary temp array with the same size as the original array arr
  • Define auxiliary pointer i to traverse arr1 and auxiliary pointer j to traverse arr2. The principle is to put the numbers in arr1 and arr2 into temp so that temp[left] ~ temp[right] are ordered arrays
  • Finally, copy the data in the temp temporary array back to the original array (personally, it's OK to copy it back next time...)

• How?

  • Left recursive splitting: mergeSort(arr, left, mid, temp);
  • Right recursive splitting: mergeSort(arr, mid + 1, right, temp);

8.4 code implementation

8.4.1 compile merge sorting algorithm

• Merge sort algorithm implementation code

public class MergetSort {

	public static void main(String[] args) {
        
		int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 };
		int temp[] = new int[arr.length]; // Merge sort requires an extra space
		mergeSort(arr, 0, arr.length - 1, temp);
		System.out.println("After merging and sorting=" + Arrays.toString(arr));

	}

	// Opening + closing method
	public static void mergeSort(int[] arr, int left, int right, int[] temp) {
		if (left < right) {
			int mid = (left + right) / 2; // Intermediate index
			// Decompose recursively to the left
			mergeSort(arr, left, mid, temp);
			// Decompose recursively to the right
			mergeSort(arr, mid + 1, right, temp);
			// merge
			merge(arr, left, mid, right, temp);
		}
	}

	// Merging method
	/**
	 * 
	 * @param arr   Sorted original array
	 * @param left  Initial index of left ordered sequence
	 * @param mid   Intermediate index
	 * @param right Right index
	 * @param temp  Array for transit
	 */
	public static void merge(int[] arr, int left, int mid, int right, int[] temp) {

		int i = left; // Initialization i, the initial index of the left ordered sequence
		int j = mid + 1; // Initialization j, the initial index of the ordered sequence on the right
		int t = 0; // Points to the current index of the temp array

		// (I)
		// First, fill the left and right (ordered) data into the temp array according to the rules
		// Until one side of the ordered sequence on the left and right is processed
		while (i <= mid && j <= right) {// continue
			// If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
			// Fill the current element on the left into the temp array
			// Then t++, i++
			if (arr[i] <= arr[j]) {
				temp[t] = arr[i];
				t += 1;
				i += 1;
			} else { // On the contrary, fill the current element of the ordered sequence on the right into the temp array
				temp[t] = arr[j];
				t += 1;
				j += 1;
			}
		}

		// (II)
		// Fill all the data on the side with remaining data into temp in turn
		while (i <= mid) { // The ordered sequence on the left and the remaining elements are filled into temp
			temp[t] = arr[i];
			t += 1;
			i += 1;
		}

		while (j <= right) { // The ordered sequence on the right and the remaining elements are filled into temp
			temp[t] = arr[j];
			t += 1;
			j += 1;
		}

		// (III)
		// Copy the elements of temp array to arr
		// Note that not all are copied every time
		t = 0;
		int tempLeft = left; //
		// The first time: templeft = 0, right = 1 / / the second time: templeft = 2, right = 3 / / the third time: TL = 0, RI = 3
		// Last tempLeft = 0 right = 7
		while (tempLeft <= right) {
			arr[tempLeft] = temp[t];
			t += 1;
			tempLeft += 1;
		}

	}

}

• Program running results

After merging and sorting=[1, 2, 3, 4, 5, 6, 7, 8]

8.4.2 test the merging and sorting performance

• Test the performance of merge sorting algorithm

public class MergetSort {

    public static void main(String[] args) {

        // Test the execution speed of fast platoon
        // Create a random array to give 80000
        int[] arr = new int[8000000];
        for (int i = 0; i < 8000000; i++) {
            arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
        }
        System.out.println("Before sorting");
        Date data1 = new Date();
        SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String date1Str = simpleDateFormat.format(data1);
        System.out.println("The time before sorting is=" + date1Str);

        int temp[] = new int[arr.length]; // Merge sort requires an extra space
        mergeSort(arr, 0, arr.length - 1, temp);

        Date data2 = new Date();
        String date2Str = simpleDateFormat.format(data2);
        System.out.println("The time before sorting is=" + date2Str);

        // System.out.println("after merging and sorting =" + Arrays.toString(arr));
    }

    // Opening + closing method
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            int mid = (left + right) / 2; // Intermediate index
            // Decompose recursively to the left
            mergeSort(arr, left, mid, temp);
            // Decompose recursively to the right
            mergeSort(arr, mid + 1, right, temp);
            // merge
            merge(arr, left, mid, right, temp);
        }
    }

    // Merging method

    /**
     *
     * @param arr   Sorted original array
     * @param left  Initial index of left ordered sequence
     * @param mid   Intermediate index
     * @param right Right index
     * @param temp  Array for transit
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {

        int i = left; // Initialization i, the initial index of the left ordered sequence
        int j = mid + 1; // Initialization j, the initial index of the ordered sequence on the right
        int t = 0; // Points to the current index of the temp array

        // (I)
        // First, fill the left and right (ordered) data into the temp array according to the rules
        // Until one side of the ordered sequence on the left and right is processed
        while (i <= mid && j <= right) {// continue
            // If the current element of the left ordered sequence is less than or equal to the current element of the right ordered sequence
            // Fill the current element on the left into the temp array
            // Then t++, i++
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { // On the contrary, fill the current element of the ordered sequence on the right into the temp array
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }

        // (II)
        // Fill all the data on the side with remaining data into temp in turn
        while (i <= mid) { // The ordered sequence on the left and the remaining elements are filled into temp
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }

        while (j <= right) { // The ordered sequence on the right and the remaining elements are filled into temp
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }

        // (III)
        // Copy the elements of temp array to arr
        // Note that not all are copied every time
        t = 0;
        int tempLeft = left; //
        // The first time: templeft = 0, right = 1 / / the second time: templeft = 2, right = 3 / / the third time: TL = 0, RI = 3
        // Last tempLeft = 0 right = 7
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft += 1;
        }

    }

}

• Program running results: eight million data took 1s, which is also very fast

Before sorting
 The time before sorting is=2020-07-16 16:18:32
 The time before sorting is=2020-07-16 16:18:33

8.5 summary

• First divide the array into left and right halves, and first perform left half recursion:
  • First, execute left recursion to the deepest layer. If the condition if (left < right) is not satisfied, start merging, merge {8,4} into the temporary array temp, change it into an ordered array {4,8}, and then copy it back to the original array arr
  • Then, execute the deepest right recursion. If the condition if (left < right) is not satisfied, start merging, merge {5,7} into the temporary array temp, change it into an ordered array {2,7}, and then copy it back to the original array arr
  • After merging, recursively backtrack to the previous section and start merging. Merge {4,5,7,8} into the temporary array temp, change it into an ordered array {4,5,7,8}, and then copy it back to the original array arr
• The same is true for recursion on the right and left sides

9. Cardinality sort

9.1 basic introduction to cardinality sorting

• radix sort belongs to "distribution sort", also known as "bucket sort" or bin sort. As the name suggests, it is the value of each bit of the key value,
  Assign the elements to be sorted to some "buckets" to sort
• Cardinal ranking method belongs to stable ranking, and cardinal ranking method is a stable ranking method with high efficiency
• Radix sort is an extension of bucket sort
• Cardinality sorting was invented by Herman hollery in 1887. It is implemented in this way: the integer is cut into different numbers according to the number of bits, and then compared according to each number of bits.

9.2 cardinality sorting idea

• Unify all values to be compared into the same digit length, and fill zero in front of the shorter digit.
• Then, start from the lowest order and sort once in turn. In this way, the sequence becomes an ordered sequence from the lowest order to the highest order.

9.3 cardinality sorting diagram

• There are 10 barrels with corresponding numbers of 0 ~ 9

• step

  • Step 1: according to the single digit of each element in the original array arr, put it into buckets 0 ~ 9 in turn (each bucket is placed from front to back). After placement, take out the data in the bucket in turn (each bucket is taken from the back) and put it back into the original array arr, so that the original array arr
    The single digit elements are already arranged in order
  • Step 2: according to the ten digits of each element in the original array arr, put it into buckets 0 ~ 9 in turn (each bucket is placed from front to back). After placement, take out the data in the bucket in turn (each bucket is taken from the back) and put it back into the original array arr, so that the ten digits in the original array arr+
    The single digit elements are already arranged in order
  • Step 3: according to the hundredths of each element in the original array arr, put it into buckets 0 ~ 9 in turn (each bucket is placed from front to back). After placement, take out the data in the bucket in turn (each bucket is taken from the back) and put it back into the original array arr, so that the hundredths of the original array arr + tens+
    The single digit elements are already arranged in order
  • ...

• When is the sorting complete? When the elements with the longest digits in the array are processed, the sorting is completed

• How to determine the capacity of the barrel? Assuming that the number of bits of each element of the array is the same, the maximum capacity of a single bucket is the array capacity. We use a two-dimensional array to represent the bucket: int[][] bucket = new int[10][arr.length];

• How do we know how many elements are in a barrel? This also requires records, which are recorded with a one-dimensional array:

  int[] bucketElementCounts = new int[10];

• Summary:

  • Assuming that the longest digit of the elements in the array is maxLength, after processing the maxLength digit, the array sorting is completed: for (int, I = 0, n = 1; I < maxLength; I + +, n * = 10){

  • Use a for loop to process the original one-dimensional array arr and put it into the bucket

    for(int j = 0; j < arr.length; j++) {

  • Use a two-layer for loop to process 10 buckets and put the elements back into the original one-dimensional array

    for (int k = 0; k < bucketElementCounts.length; k++) {
    if (bucketElementCounts[k] != 0) {
    for (int l = 0; l < bucketElementCounts[k]; l++) {

9.4 code implementation

9.4.1 understand cardinality sorting

• Step by step decomposition, understand the cardinality sorting algorithm

public class RadixSort {

    public static void main(String[] args) {

        int arr[] = {53, 3, 542, 748, 14, 214};
        radixSort(arr);
        System.out.println("After cardinality sorting " + Arrays.toString(arr));

    }

    //Cardinality sorting method
    public static void radixSort(int[] arr) {

//		//According to the previous derivation process, we can get the final cardinality sorting code

        //1. Get the number of digits of the largest number in the array
        int max = arr[0]; //Suppose the first number is the maximum number
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }

        //Define a two-dimensional array, representing 10 buckets, and each bucket is a one-dimensional array
        //explain
        //1. The two-dimensional array contains 10 one-dimensional arrays
        //2. In order to prevent data overflow when putting in numbers, the size of each one-dimensional array (bucket) is set to arr.length
        //3. The name is clear, and cardinality sorting is a classical algorithm that uses space for time
        int[][] bucket = new int[10][arr.length];

        //In order to record how many data are actually stored in each bucket, we define a one-dimensional array to record the number of data put in each bucket
        //It can be understood here
        //For example, bucketElementCounts[0] records the number of data put into the bucket[0]
        int[] bucketElementCounts = new int[10];


        //Round 1 (sort the bits of each element)
        for (int j = 0; j < arr.length; j++) {
            //Take out the value of one bit of each element
            int digitOfElement = arr[j] / 1 % 10;
            //Put it into the corresponding bucket
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            bucketElementCounts[digitOfElement]++;
        }
        //According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
        int index = 0;
        //Traverse each bucket, and put the data in the bucket into the original array
        for (int k = 0; k < bucketElementCounts.length; k++) {
            //If there is data in the bucket, we put it into the original array
            if (bucketElementCounts[k] != 0) {
                //Loop the bucket, i.e. the k-th bucket (i.e. the k-th one-dimensional array), and put it into
                for (int l = 0; l < bucketElementCounts[k]; l++) {
                    //Take out the element and put it into the arr
                    arr[index++] = bucket[k][l];
                }
            }
            //After the 1st round of processing, each bucket e l ementcounts [k] = 0!!!!
            bucketElementCounts[k] = 0;
        }
        System.out.println("Round 1: sorting of individual bits arr =" + Arrays.toString(arr));


        //Round 2 (sort the ten bits of each element)
        for (int j = 0; j < arr.length; j++) {
            // Take out the ten digit value of each element
            int digitOfElement = arr[j] / 10 % 10; //748 / 10 => 74 % 10 => 4
            // Put it into the corresponding bucket
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            bucketElementCounts[digitOfElement]++;
        }
        // According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
        index = 0;
        // Traverse each bucket, and put the data in the bucket into the original array
        for (int k = 0; k < bucketElementCounts.length; k++) {
            // If there is data in the bucket, we put it into the original array
            if (bucketElementCounts[k] != 0) {
                // Loop the bucket, i.e. the k-th bucket (i.e. the k-th one-dimensional array), and put it into
                for (int l = 0; l < bucketElementCounts[k]; l++) {
                    // Take out the element and put it into the arr
                    arr[index++] = bucket[k][l];
                }
            }
            //After the second round of processing, each bucket elementcounts [k] = 0!!!!
            bucketElementCounts[k] = 0;
        }
        System.out.println("Round 2: sorting of individual bits arr =" + Arrays.toString(arr));


        //Round 3 (sort the hundreds of each element)
        for (int j = 0; j < arr.length; j++) {
            // Take out the value of the hundredth of each element
            int digitOfElement = arr[j] / 100 % 10; // 748 / 100 => 7 % 10 = 7
            // Put it into the corresponding bucket
            bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
            bucketElementCounts[digitOfElement]++;
        }
        // According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
        index = 0;
        // Traverse each bucket, and put the data in the bucket into the original array
        for (int k = 0; k < bucketElementCounts.length; k++) {
            // If there is data in the bucket, we put it into the original array
            if (bucketElementCounts[k] != 0) {
                // Loop the bucket, i.e. the k-th bucket (i.e. the k-th one-dimensional array), and put it into
                for (int l = 0; l < bucketElementCounts[k]; l++) {
                    // Take out the element and put it into the arr
                    arr[index++] = bucket[k][l];
                }
            }
            //After the third round of processing, each bucket elementcounts [k] = 0!!!!
            bucketElementCounts[k] = 0;
        }
        System.out.println("Round 3: sorting of individual bits arr =" + Arrays.toString(arr));
    }

}

• Program running results

Round 1: sorting of individual bits arr =[542, 53, 3, 14, 214, 748]
Round 2: sorting of individual bits arr =[3, 14, 214, 542, 748, 53]
Round 3: sorting of individual bits arr =[3, 14, 53, 214, 542, 748]
After cardinality sorting [3, 14, 53, 214, 542, 748]

9.4.2. Compiling cardinality sorting

• Write cardinality sorting algorithm

public class RadixSort {

	public static void main(String[] args) {

		int arr[] = { 53, 3, 542, 748, 14, 214 };
		radixSort(arr);
		System.out.println("After cardinality sorting " + Arrays.toString(arr));

	}

	// Cardinality sorting method
	public static void radixSort(int[] arr) {
		
		//According to the previous derivation process, we can get the final cardinality sorting code	
		//1. Get the number of digits of the largest number in the array
		int max = arr[0]; //Suppose the first number is the maximum number
		for(int i = 1; i < arr.length; i++) {
			if (arr[i] > max) {
				max = arr[i];
			}
		}
		//What is the maximum number
		int maxLength = (max + "").length();
		
		//Define a two-dimensional array, representing 10 buckets, and each bucket is a one-dimensional array
		//explain
		//1. The two-dimensional array contains 10 one-dimensional arrays
		//2. In order to prevent data overflow when putting in numbers, the size of each one-dimensional array (bucket) is set to arr.length
		//3. The name is clear, and cardinality sorting is a classical algorithm that uses space for time
		int[][] bucket = new int[10][arr.length];
		
		//In order to record how many data are actually stored in each bucket, we define a one-dimensional array to record the number of data put in each bucket
		//It can be understood here
		//For example, bucketElementCounts[0] records the number of data put into the bucket[0]
		int[] bucketElementCounts = new int[10];
		
		
		// n=1 indicates processing bits, n=10 indicates processing ten bits, n=100 indicates processing hundreds
		for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
			//(sort the corresponding bits of each element). The first is a bit, the second is a ten bit, and the third is a hundred bit
			for(int j = 0; j < arr.length; j++) {
				//Take out the value of the corresponding bit of each element
				int digitOfElement = arr[j] / n % 10;
				//Put it into the corresponding bucket
				bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
				bucketElementCounts[digitOfElement]++;
			}
			//According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
			int index = 0;
			//Traverse each bucket and put the data in the bucket into the original array
			for(int k = 0; k < bucketElementCounts.length; k++) {
				//If there is data in the bucket, we put it into the original array
				// Traverse the kth bucket (i.e. the kth one-dimensional array) and put the data in the bucket back into the original array
				for (int l = 0; l < bucketElementCounts[k]; l++) {
					// Take out the element and put it into the arr
					arr[index++] = bucket[k][l];
				}
				//After the i+1 round of processing, each bucket elementcounts [k] = 0!!!!
				bucketElementCounts[k] = 0;				
			}
			System.out.println("The first"+(i+1)+"Round, sorting of individual bits arr =" + Arrays.toString(arr));
		}
	}
	
}

• Program running results

Round 1: sorting of individual bits arr =[542, 53, 3, 14, 214, 748]
Round 2: sorting of individual bits arr =[3, 14, 214, 542, 748, 53]
Round 3: sorting of individual bits arr =[3, 14, 53, 214, 542, 748]
After cardinality sorting [3, 14, 53, 214, 542, 748]

9.4.3 test cardinality sorting performance

• Test the performance of cardinality sorting algorithm

public class RadixSort {

	public static void main(String[] args) {

		// 80000000 * 11 * 4 / 1024 / 1024 / 1024 =3.3G 
		int[] arr = new int[8000000];
		for (int i = 0; i < 8000000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // Generate a [0, 8000000) number
		}
		System.out.println("Before sorting");
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("The time before sorting is=" + date1Str);
		
		radixSort(arr);
		
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("The time before sorting is=" + date2Str);
		

	}

	// Cardinality sorting method
	public static void radixSort(int[] arr) {
		
		//According to the previous derivation process, we can get the final cardinality sorting code	
		//1. Get the number of digits of the largest number in the array
		int max = arr[0]; //Suppose the first number is the maximum number
		for(int i = 1; i < arr.length; i++) {
			if (arr[i] > max) {
				max = arr[i];
			}
		}
		//What is the maximum number
		int maxLength = (max + "").length();
		
		//Define a two-dimensional array, representing 10 buckets, and each bucket is a one-dimensional array
		//explain
		//1. The two-dimensional array contains 10 one-dimensional arrays
		//2. In order to prevent data overflow when putting in numbers, the size of each one-dimensional array (bucket) is set to arr.length
		//3. The name is clear, and cardinality sorting is a classical algorithm that uses space for time
		int[][] bucket = new int[10][arr.length];
		
		//In order to record how many data are actually stored in each bucket, we define a one-dimensional array to record the number of data put in each bucket
		//It can be understood here
		//For example, bucketElementCounts[0] records the number of data put into the bucket[0]
		int[] bucketElementCounts = new int[10];
		
		
		// n=1 indicates processing bits, n=10 indicates processing ten bits, n=100 indicates processing hundreds
		for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {
			//(sort the corresponding bits of each element). The first is a bit, the second is a ten bit, and the third is a hundred bit
			for(int j = 0; j < arr.length; j++) {
				//Take out the value of the corresponding bit of each element
				int digitOfElement = arr[j] / n % 10;
				//Put it into the corresponding bucket
				bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
				bucketElementCounts[digitOfElement]++;
			}
			//According to the order of the bucket (the subscripts of the one-dimensional array take out the data in turn and put it into the original array)
			int index = 0;
			//Traverse each bucket and put the data in the bucket into the original array
			for(int k = 0; k < bucketElementCounts.length; k++) {
				//If there is data in the bucket, we put it into the original array
				// Traverse the kth bucket (i.e. the kth one-dimensional array) and put the data in the bucket back into the original array
				for (int l = 0; l < bucketElementCounts[k]; l++) {
					// Take out the element and put it into the arr
					arr[index++] = bucket[k][l];
				}
				//After the i+1 round of processing, each bucket elementcounts [k] = 0!!!!
				bucketElementCounts[k] = 0;				
			}
			System.out.println("The first"+(i+1)+"Round, sorting of individual bits arr =" + Arrays.toString(arr));
		}
	}
	
}

• Program running results: Yes, eight million data are arranged in 1s, but it takes up too much space

Before sorting
 The time before sorting is=2020-07-16 18:16:21
 The time before sorting is=2020-07-16 18:16:22

9.5. Description of cardinality sorting

• Cardinality sorting is an extension of traditional bucket sorting, which is very fast
• Cardinality sorting is a classic space for time method, which takes up a lot of memory. When sorting massive data, it is easy to cause OutOfMemoryError.
• Cardinality sorting is stable. [Note: it is assumed that there are multiple records with the same keyword in the record sequence to be sorted. If sorted, the relative order of these records remains unchanged, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still
  Before r[j], this sort algorithm is called stable; otherwise, it is called unstable]
• For arrays with negative numbers, we do not use cardinality sorting. If you want to support negative numbers, refer to: https://code.i-harness.com/zh-CN/q/e98fa9

10. Summary and comparison of common sorting algorithms

10.1 comparison diagram of sorting algorithms

10.2 interpretation of relevant terms

• Stable: if a is in front of b and a=b, a is still in front of b after sorting;
• Unstable: if a was originally in front of b and a=b, a may appear after b after sorting;
• Internal sorting: all sorting operations are completed in memory;
• External sorting: because the data is too large, the data is placed on the disk, and the sorting can only be carried out through the data transmission of disk and memory;
• Time complexity: the time spent in the execution of an algorithm.
• Space complexity: the amount of memory required to run a program.
• n: Data scale
• k: Number of "barrels"
• In place: no extra memory
• Out place: use additional memory