Chapter 3 stack and queue
Stacks and queues are linear tables that restrict inserts and deletions to the "end" (end) of the table
That is, stacks and queues are subsets of linear tables (linear tables with restricted insertion and deletion positions)
Stack features: first in, last out
Queue characteristics: first in first out
3.1 definition and characteristics of stack and queue
3.1.1 definition and characteristics of stack
1. The definition can only be operated at the top of the stack
2. Logical structure one-to-one
3. Storage structure sequence stack or chain stack. Sequence stack is more common
4. Operation rules can only be operated at the top of the stack, and the principle of "last in, first out" is followed when accessing nodes
5. The key to the implementation method is to write the stack in and stack out functions. The specific implementation varies according to the storage structure
Operation diagram of stack
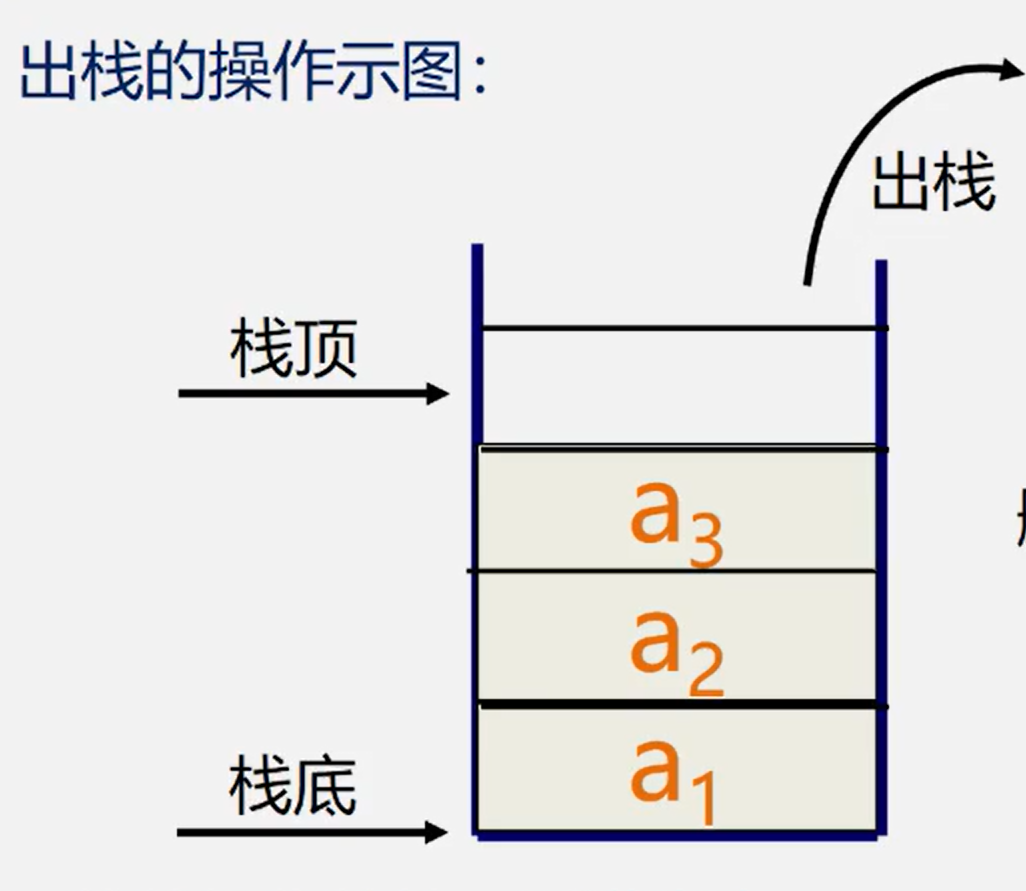
The difference between stack and general linear table is only that the operation rules are different

3.1.2 definition and characteristics of queue
1. Insert one end of the definition table and delete the other end (head deletion and tail insertion)
2. Logical structure one-to-one
3. Storage structure sequence team or chain team, cyclic sequence team is more common
4. Operation rules can only be operated at the top of the stack, and the principle of "last in, first out" is followed when accessing nodes
5. The key to the implementation method is to master the operation of joining and leaving the team. The specific implementation varies according to the order of the team and the chain team
3.2 stack representation and operation implementation
3.2.1 representation and implementation of sequence stack
Set the top pointer to point to the position of the top element of the stack
Set the base pointer to point to the position of the element at the bottom of the stack (for ease of operation, top usually points to the subscript address above the element at the top of the stack)
Stack size is used to represent the maximum capacity of the stack
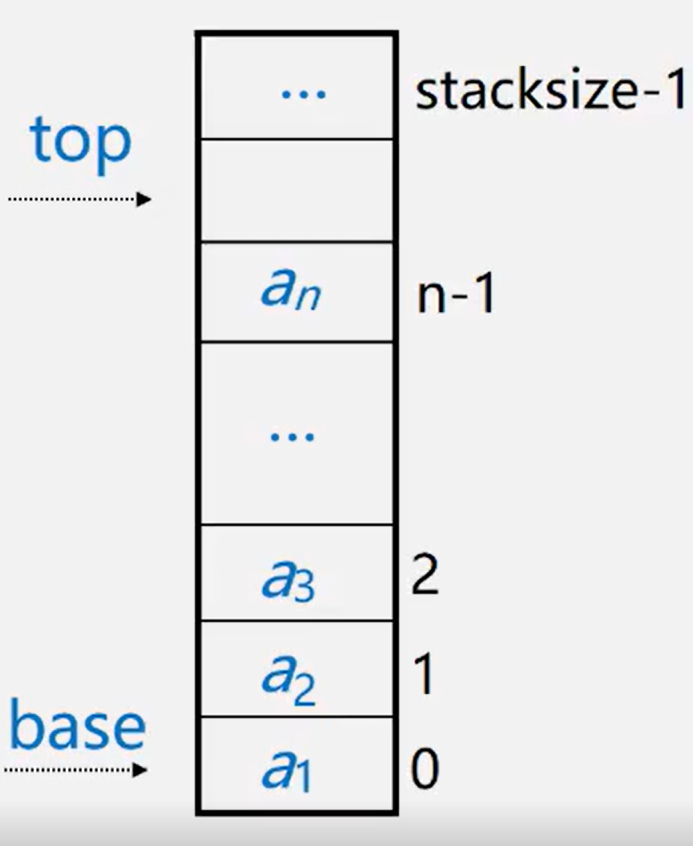
Empty stack: base == top is an empty stack
Stack full: top - base == stacksize
Stack full processing method:
- An error is reported. The stack overflows
- Allocate more space and transfer the contents of the original stack to the new stack
Overflow is divided into overflow and underflow
Overflow: the stack is full, and there are new elements pressing the stack
Underflow: if the stack is empty, you have to play the stack
Note: overflow is an error that prevents problem handling; Underflow is an end condition, that is, the end of problem processing
3.2.2 algorithm
Representation of sequential stack
# define MAXSIZE 100
typedef struct{
SElemType *base; //Stack bottom pointer
SElemType *top; //Stack top pointer
int stacksize; //Maximum available stack capacity
}SqStack
3.2.2.1 initialization of sequence stack
Status InitStack(SqStack &S){ // Construct an empty stack
S.base = new SElemType[MAXSIEZE];
if (!S.base) exit (OVERFLOW); // Storage allocation failed
S.top = S.base //Stack top pointer equals stack bottom pointer
S.stacksize = MAXSIZE;
return OK;
}
3.2.2.2 determine whether the sequence stack is empty
Status StackEmpty(SqStack S){
// If the stack is empty, return true; otherwise, return false
if(S.top == S.base){
return true;
else
return false;
}
3.2.2.3 sequence stack length
int StackLength(SqStack S){
return S.top - S.base;
}
3.2.2.4 clear sequence stack
Status ClearStack(SqStack S){
if(S.base)
S.top = S.base;
return OK;
}
3.2.2.5 destruction sequence stack
Status DestroyStack(SqStack S){
if(S.base){
delete S.base;
S.stacksize = 0;
S.top = S.base = null;
}
return OK;
}
Several important algorithms
3.2.2.6 stacking of sequence stack
It takes three steps to stack
1.Judge whether the stack is full. If the stack is full, an error will be reported(Overflow)
2.Stack elements(e) Endow top Pointer
3.Stack top pointer+1
Status Push(SqStack &S,SElemType e){
if(S.top - S.base == S.stacksize) //Stack full
return error;
*S.top = e;
S.top++;
return ok;
}
3.2.2.7 out of sequence stack
chu Stack requires three steps
1.Judge whether the stack is empty. If the stack is empty, an error will be reported(Underflow)
2.Get stack top element (e)
3.Stack top pointer - 1
Status POP(SqStack &S,SElemType &e){
if(S.top == S.base ) //If the stack is empty, you can check whether it is empty
return error;
--S.top;
e = *S.top;
return ok;
}
3.2.3 representation and implementation of chain stack
Chain stack is a single linked list with limited operation. It can only be operated at the head of the linked list
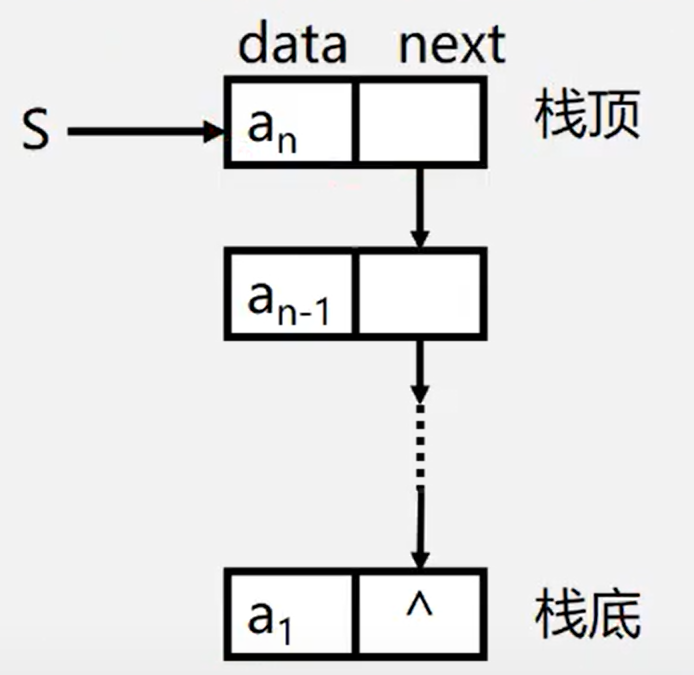
- The head pointer of the linked list is the top of the stack
- No header node is required
- The stack is basically not full
- An empty stack is equivalent to a header pointer pointing to null
- Inserts and deletions are performed only at the top of the stack
3.2.4 algorithm
3.2.4.1 initialization of chain stack
void InitStack(LinkStack &s){
S=NULL;
return OK;
}
3.2.4.2 judge whether the chain stack is empty
Status StackEmpty(LinkStack S){
if(S==NULL) return true;
else return false
}
3.2.4.3 chain stacking
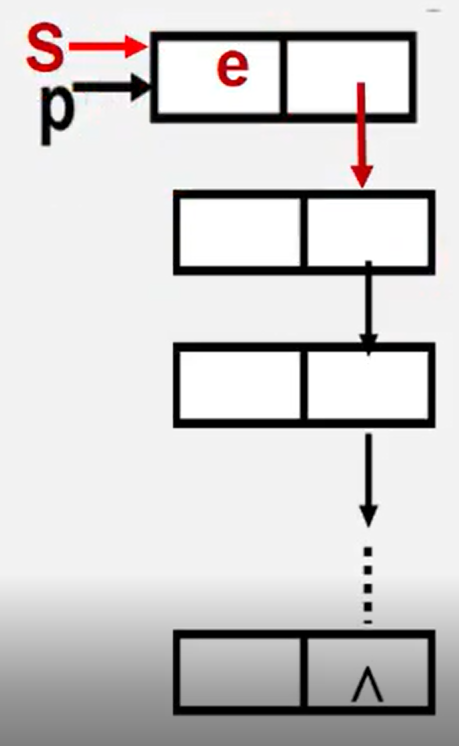
Status Push(LinkStack &S, SElemType e){
p=new StackNode; //New production node P
p->data=e; //Set the new node data field to e
p->next=S; //Insert the new node into the top of the stack
S=p; //Modify stack top pointer
return OK;
}
3.2.4.4 chain stack exit
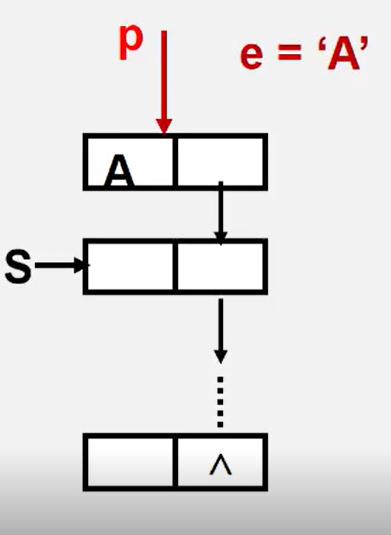
Status Pop(LinkStack &S, SElemType e){
if(S==NULL) return error;
e = S-> data;
p = S;
S = S-> next;
delete p;
return OK;
}
3.2.4.5 stack top elements
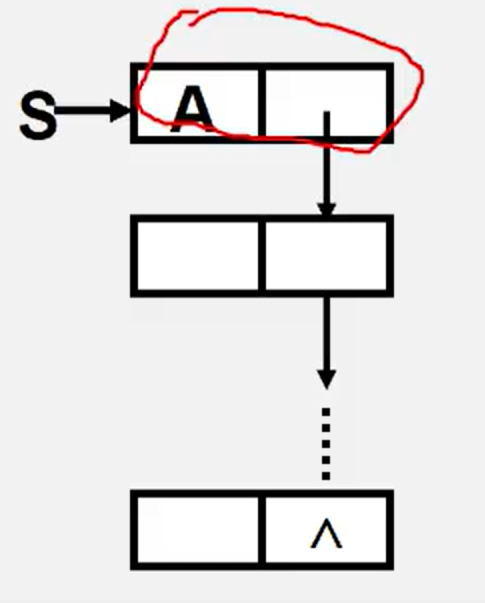
Status Pop(LinkStack &S, SElemType e){
if(S!=NULL)
return S->next;
}
3.3 stack and recursion
3.3.1 definition of recursion
-
If part of the an object contains itself, or it defines itself, object is said to be recursive
-
If a procedure calls itself directly or indirectly, it is called a recursive procedure
Recursive problem -- solved by divide and conquer method
- Divide and conquer method: for a more complex problem, it can be decomposed into several relatively simple sub problems with the same or similar solution
Three necessary conditions
- It can transform a problem into a new problem, and the solution of the new problem is the same or similar to that of the original problem. The only difference is the processing objects, and these processing objects change regularly
- The problem can be simplified through the above transformation
- There must be an explicit recursive exit, or recursive boundary
General form of algorithm for solving recursive problem by divide and conquer method:
void p(Parameter table){
if(Recursive end condition) can be solved directly -- Basic item
else p(Smaller parameter) --- inductive term
}
example: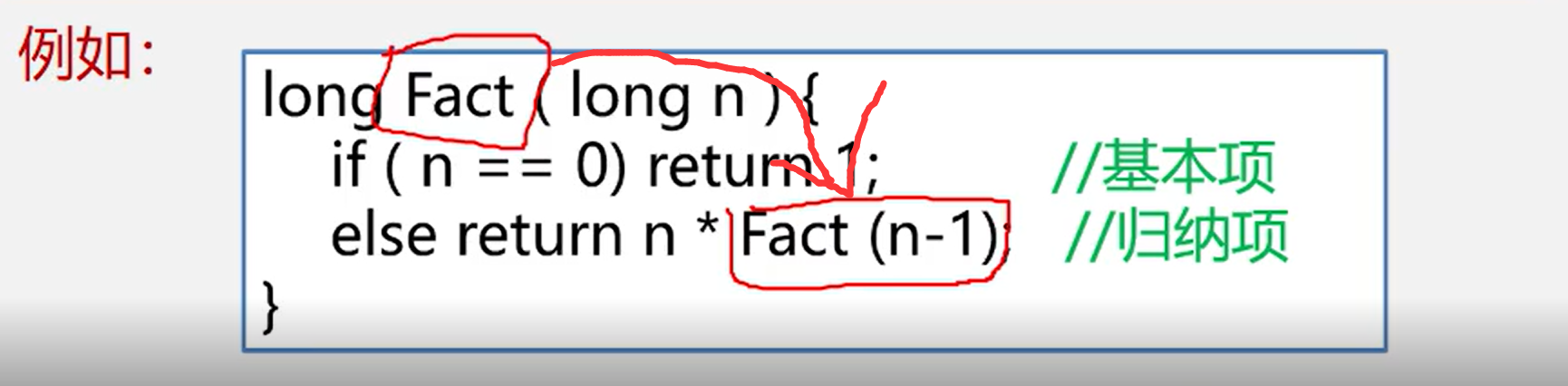
3.3.2 advantages and disadvantages of recursion
Advantages: clear structure and easy to read program
Disadvantages: each call needs to generate a work record, save the status information and put it on the stack; When returning, you need to get out of the stack and reply to the status information. High time cost
3.4 queue representation and operation implementation
Queue storage methods are divided into sequential queue and chain queue
3.4.1 representation of sequential queue
#define MAXQSIZE 100 // Maximum queue length
Typedef struct{
QElemType *base // Initialize dynamically allocated space
int front //Head pointer
int rear //Tail pointer
}SqQueue
True overflow: that is, all elements are full
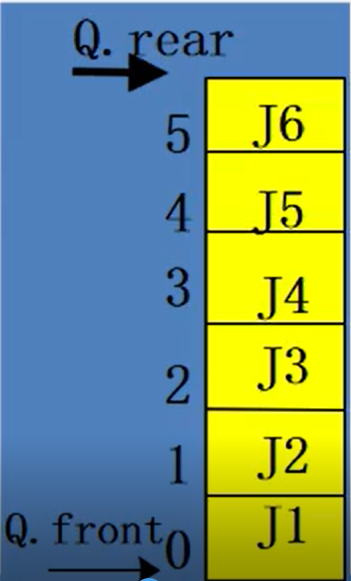
False overflow: that is, the element is not full
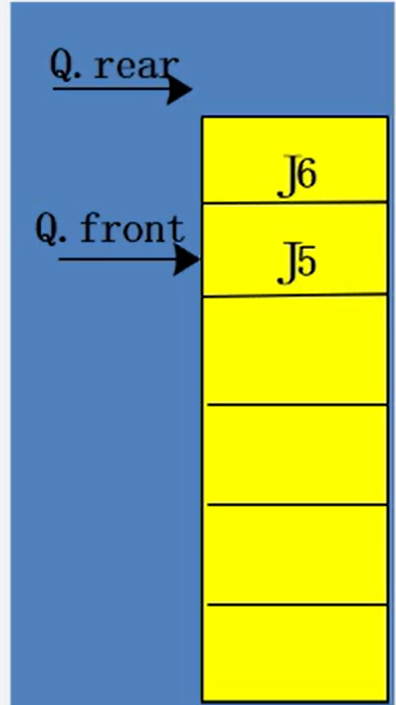
A method to solve false overflow -- circular queue
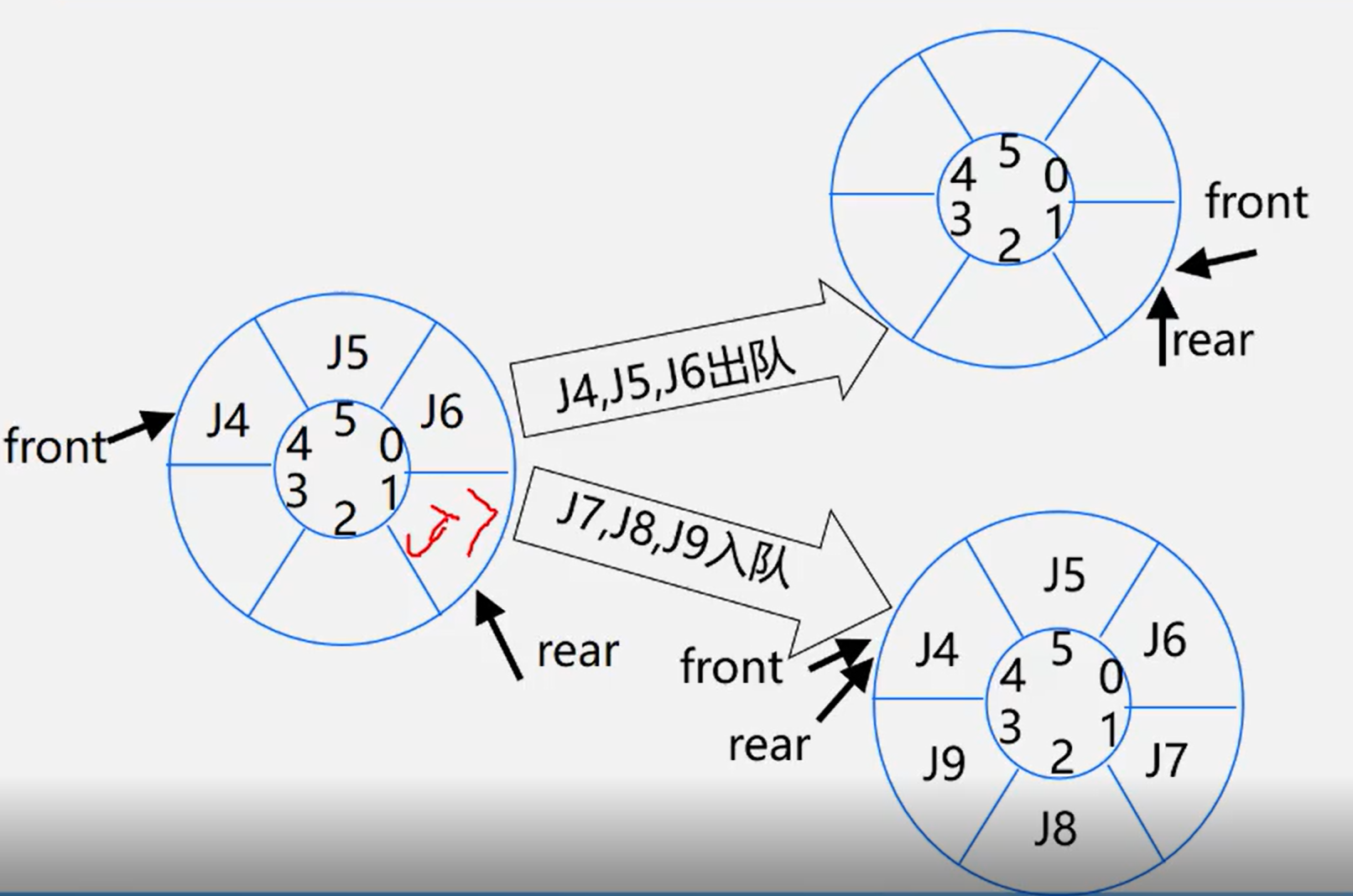
But circular queues pose a problem
Team empty: front==rear
Team full: front==rear
Solution:
1. Another sign shall be set to distinguish between empty and full teams
2. Set another variable to record the number of elements, for example: count
3. Use one less element space
3.4.2 algorithm
3.4.2.1 queue initialization
Status InitQueue(SqQueue &Q){ Q.base = new QElemType[MAXSIZE] //Allocate array space if(!Q.base) exit (OVERFLOW); // Storage allocation failed, Q.front = Q.rear = 0; // The head pointer and tail pointer are set to 0, and the queue is empty. return OK;}
3.4.2.2 calculating queue length
int InitQueue(SqQueue &Q){ return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE);}
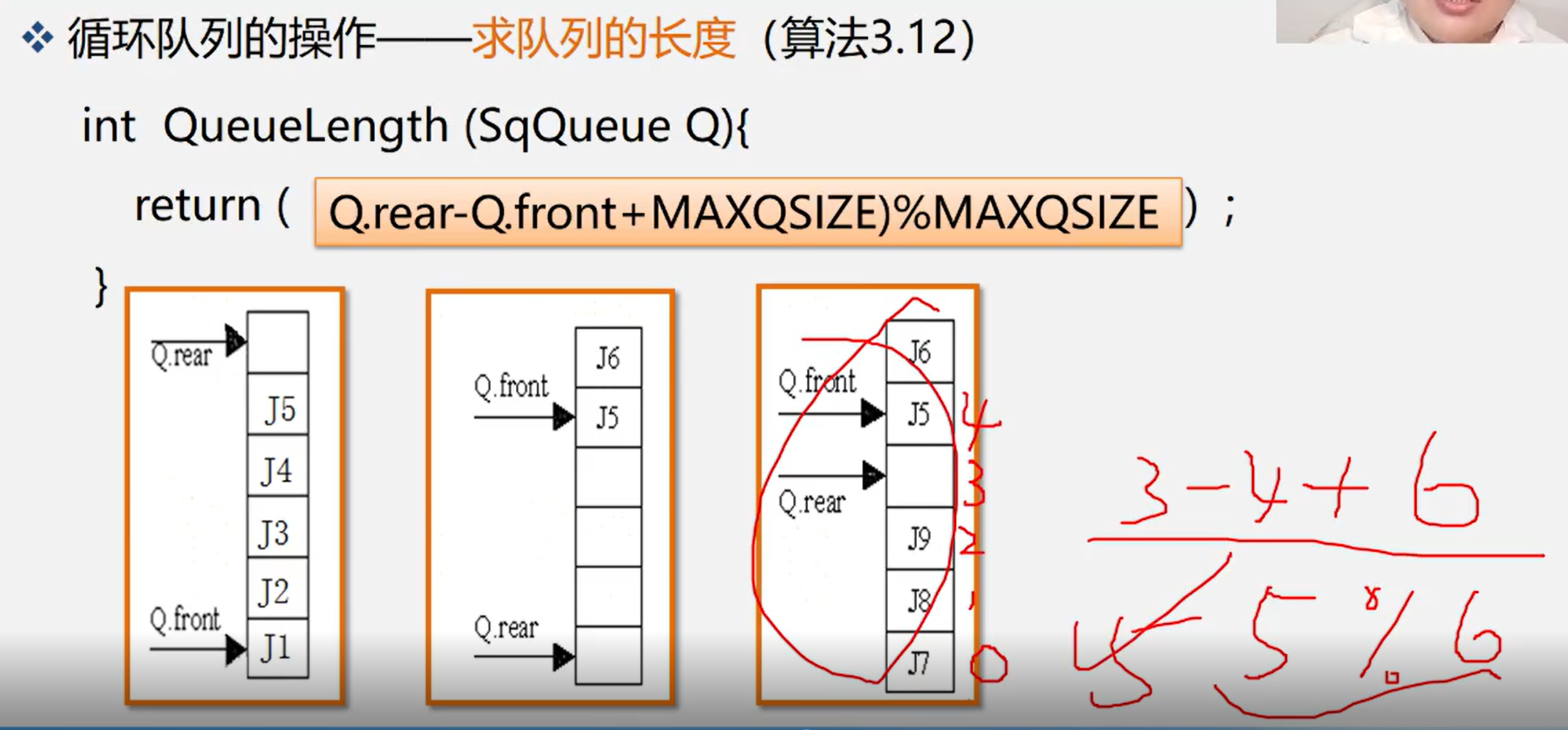
3.4.2.3 queue entry
Status EnQueue(SqQueue &Q,QElemType &e){ if((Q.rear+1)%MAXQSIZE==Q.front) return ERROR;//Team full Q.base[Q.raer]=e; // New elements are added to the tail of the team. Q.raer=(Q.raer)%MAXQSIZE; // End of line pointer + 1 return OK;}

3.4.2.4 queue out
Status DeQueue(SqQueue &Q,QElemType &e){ if(Q.front==Q.rear) return ERROR; //Team air e=Q.base[Q.front]; // Save queue header element Q.front=(Q.front+1)%MAXQSIZE // Team leader pointer + 1 return OK;}

3.4.2.5 take team head element
SElemType GetHead(SqQueue Q){ if(Q.front!=Q.rear) //Queue is not empty return Q.base[Q.front]; // Returns the value of the queue head pointer element. The queue head pointer remains unchanged}

3.4.3 representation and implementation of chain team
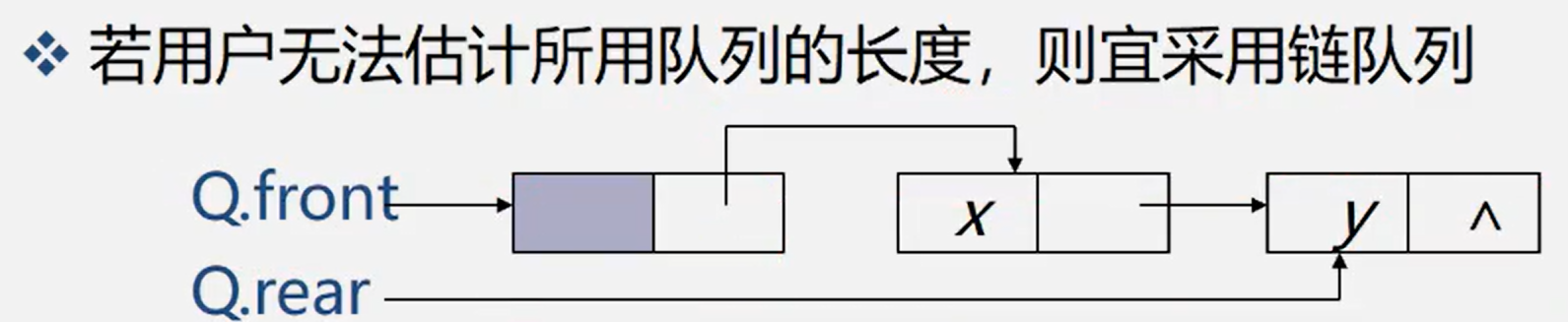
typedef struct { QuenePtr front; //Queue head pointer QuenePtr rear; // End of queue pointer} LinkQueue
3.4.4 algorithm
3.4.4.1 chain team initialization
Status InitQueue(LinkQueue &Q){ Q.front = Q.rear =(QueuePtr)malloc(sizeof(QNode)); if(!Q.front) exit (OVERFLOW); Q.front->next = NULL; return OK;}
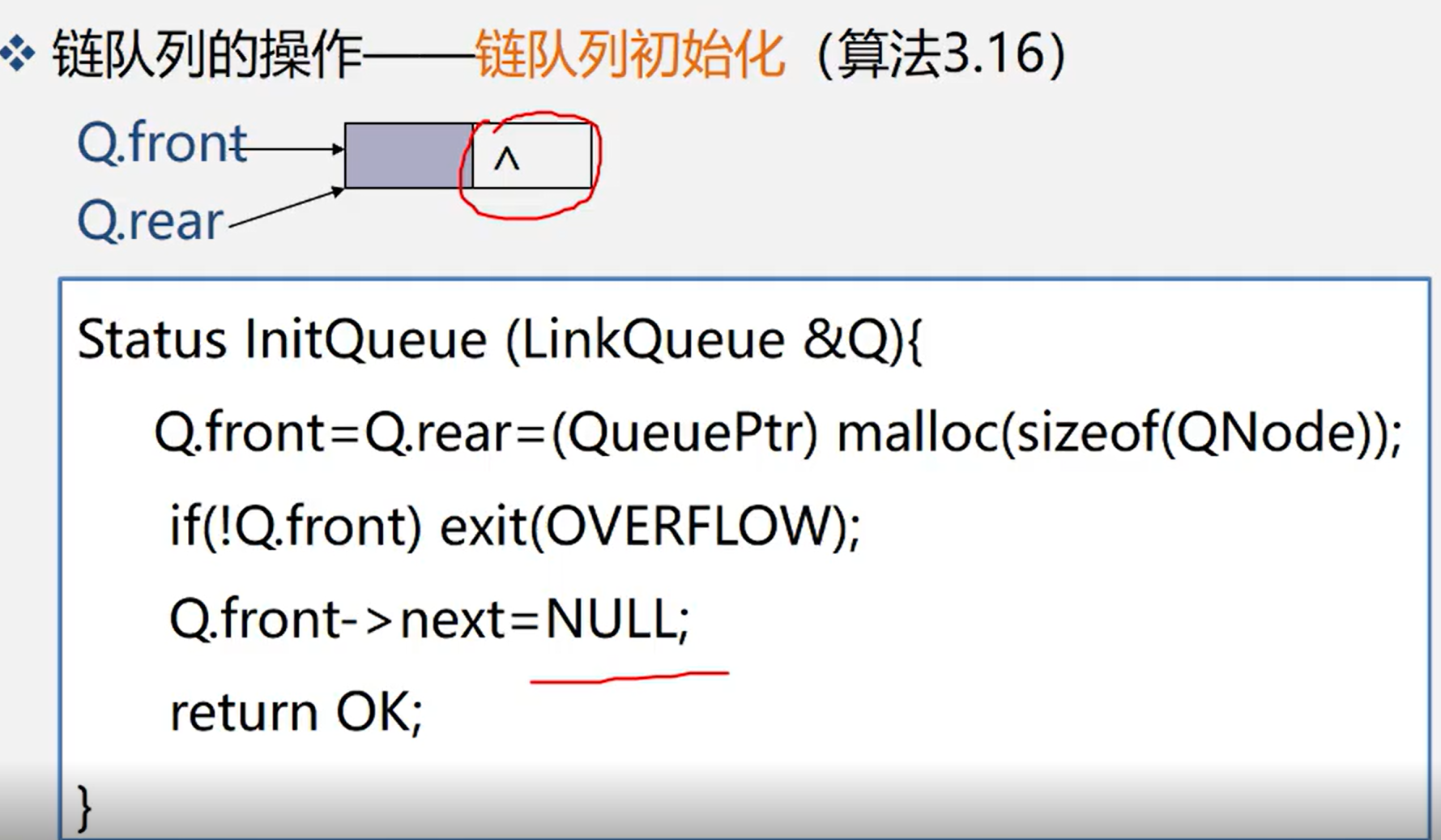
3.4.4.2 chain team destruction
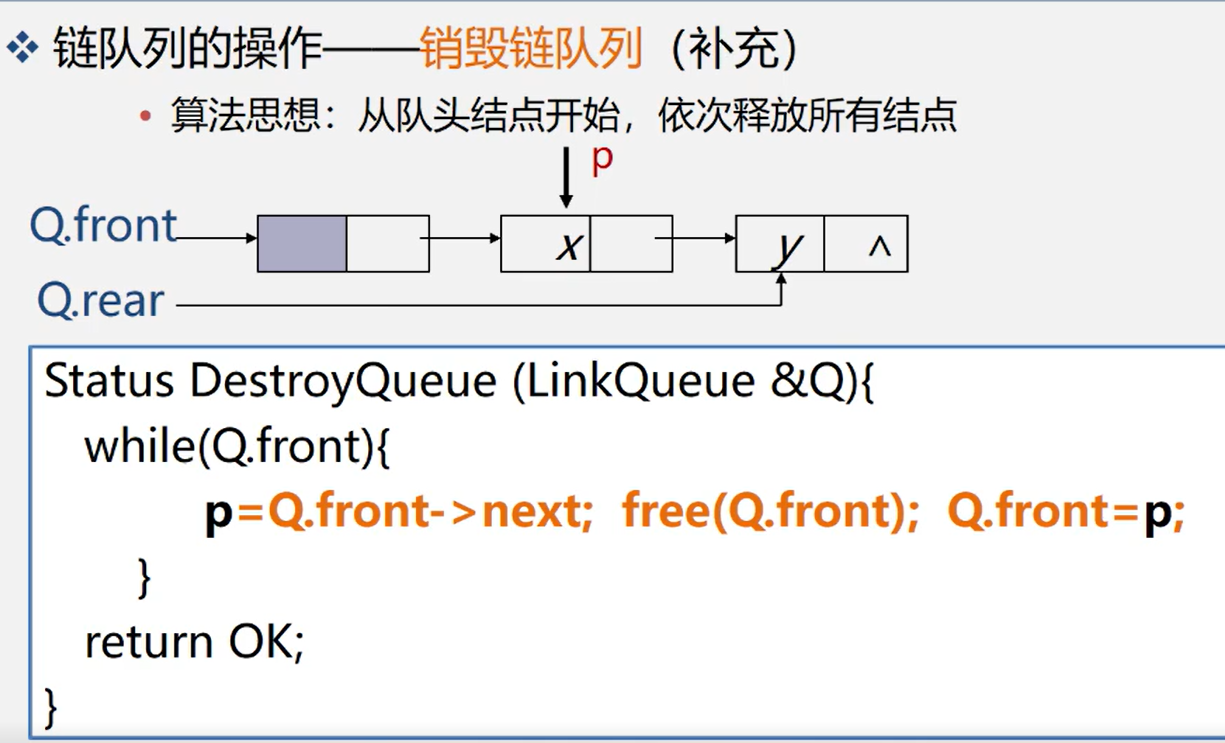
Status DestroyQueue(LinkQueue &Q){ whlie(Q.front){ p=Q.front->next; free(Q.front); Q.front-p; } return OK;}
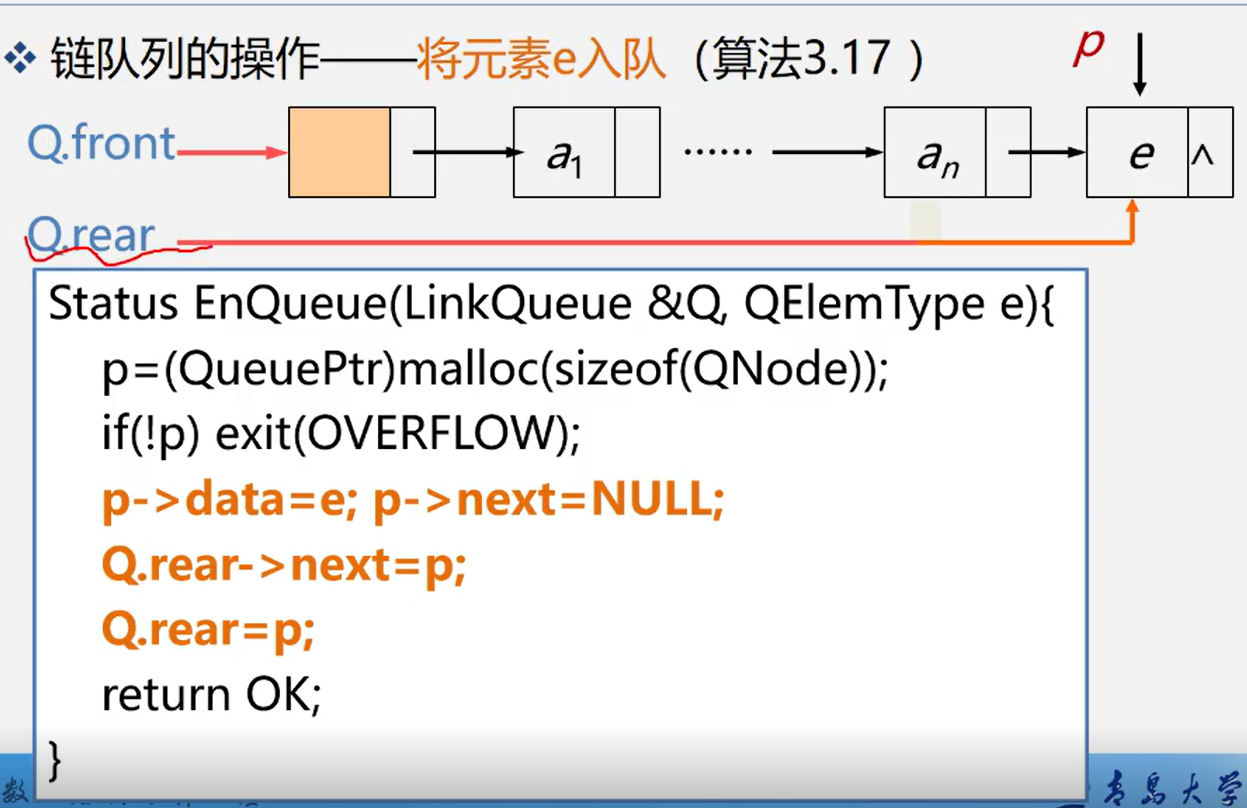
3.4.4.3 join the chain team
Status DestroyQueue(LinkQueue &Q,QElemType &e){ p=(QueuePtr)malloc(sizeof(QNode)); if(!P) exit(OVERFLOW); P->data=e; p->next=NULL; Q.rear-next=p; Q.rear=p; return OK;}
3.4.4.4 chain team out
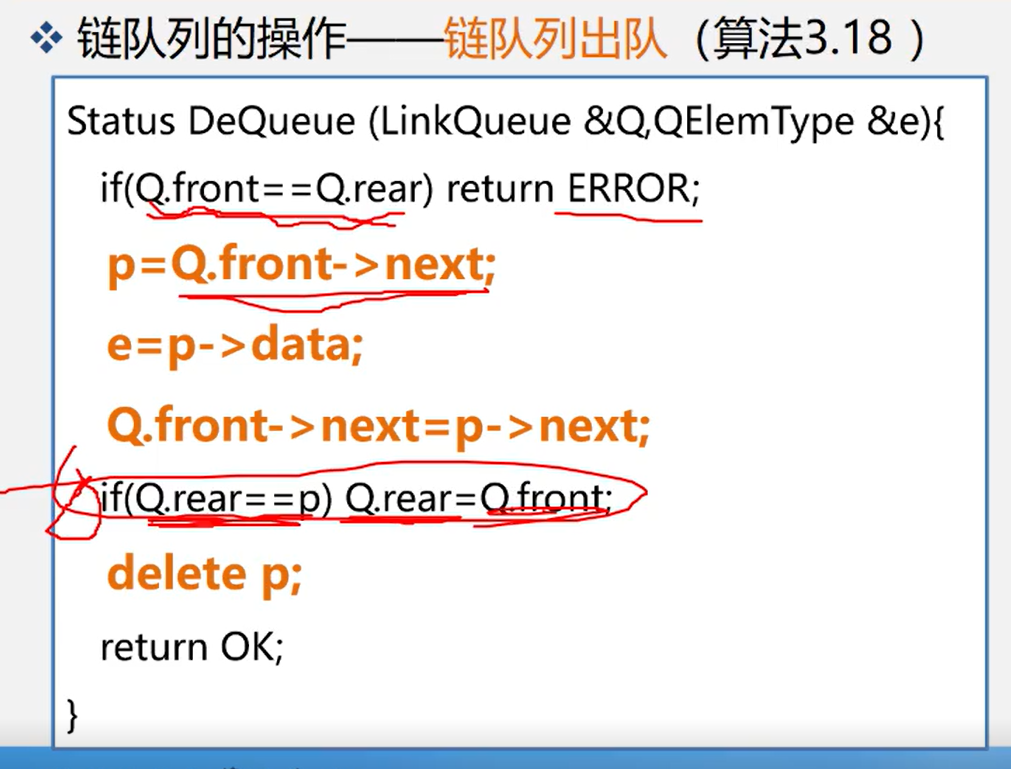
Status DestroyQueue(LinkQueue &Q,QElemType &e){ if(Q.front==Q.rear) return ERROR; p=Q.front->next; e=p->data; Q.front-next=p->next; if(Q.raer==p)Q.rear=Q.front; delete p; return OK;}
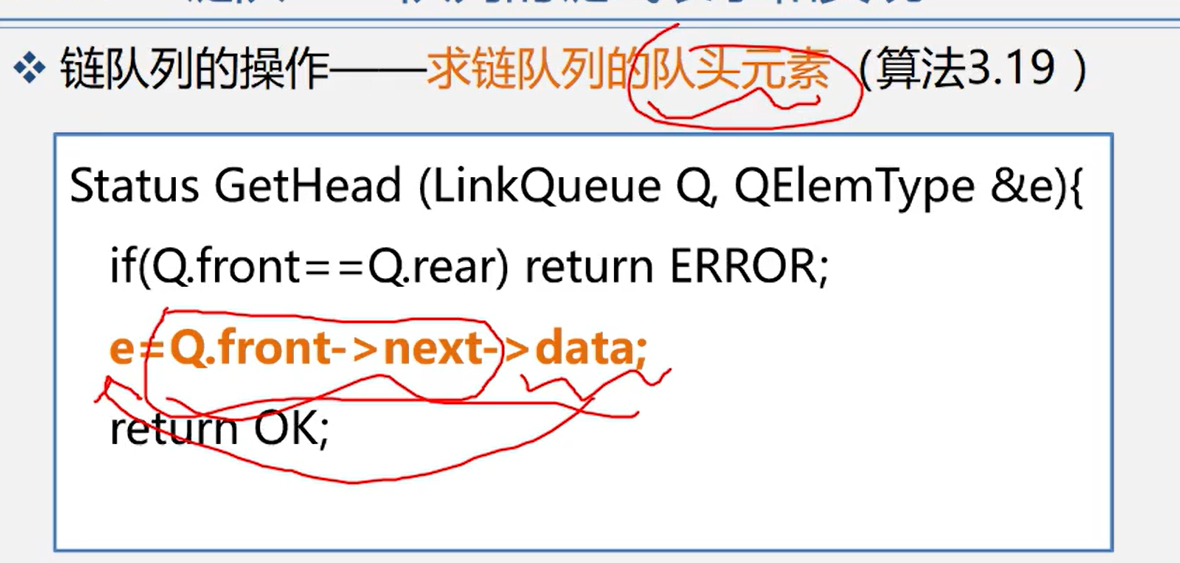
3.4.4.5 chain team take team head element
Status DestroyQueue(LinkQueue &Q,QElemType &e){ if(Q.front==Q.rear) return ERROR; e=Q.front-next->data; return OK;}