T1 statistics

subject

[Title Description]

Let S(N) denote the sum of the digits of N, such as S(484) = 4+8+4 = 16, S(22) = 2+2 = 4.

If a positive integer satisfies S(x*x) = S(x) *S(x), we call it Rabbit N umber. For example, 22 is a Rabbit N umber because S(484) = S(22) *S(22).

Now, give an interval [L, R], and find the number of Rabbit N umber in that interval.

[Input Format]

Enter only one line, two numbers L and R separated by spaces.

[Output Format]

The output is an integer in one row, representing the number of Rabbit N umber that is sought.

[Input sample]

58 484

[Output sample]

24 

[Data Scale]

1 <= L <= R <= 10^9

analysis

First reaction after reading the title: from L enumeration to R, determine whether each number is Rabbit N umber. However, the data size is 109, which is obviously timed out.

But it's okay. After finishing the violence, try to figure out the rules.

Rabbit N umber in 1-1000 is as follows:

1 2 3 10 11 12 13 20 21 22 30 31 100 101 102 103 110 111 112 113 120 121 122 130 200 201 202 210 211 212 220 221 300 301 310 311 1000

It is easy to see that no matter which one is, there is no more than 3 figures.

So there's paper-cut: any digit with more than three digits will be skipped.

So there are two approaches:

1. dfs+ paper cutting
2. Watch + Two Points

Let's not say (too much trouble) here. Let's talk about the dfs practice here.

dfs(int temp):temp can be understood as the current number is temp + a new number of digits, see the code to understand.

Starting from temp=0, each dfs function deals with a number of bits of 0.123, which satisfies the conditions and accumulates the number in the range of L~R.

After processing, if the number is less than or equal to R/10, dfs(x) (that is, the number of digits can be increased).

Finally, the total number of output would be good, don't forget to open long, as for S(x), direct simulation would be good.

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
using namespace std;
long long read()
{
    long long num=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        num=(num<<1)+(num<<3)+ch-'0';
        ch=getchar();
    }
    return num*w;
}
long long l,r,ans;
int S(long long x)
{
    int n=0;
    while(x>0)
    {
        n+=x%10;
        x/=10;    
    }
    return n;
}
void dfs(int temp)
{
    for(int i=0;i<=3;i++)
    {
        long long x=temp*10+i;
        int s=S(x);
        if(x==0||S(x*x)!=s*s) continue;
        if(l<=x&&r>=x) ans++;
        if(x<=r/10) dfs(x);
    }
}
int main()
{
    //freopen("rabbit.in","r",stdin);
    //freopen("rabbit.out","w",stdout);
    l=read(),r=read();
    dfs(0);
    cout<<ans;
    return 0;
}

T2 Digital Edge Scheme

subject

[Title Description]

Give you an undirected connected graph with n points and m edges, each edge has edge weight. Let disai denote the shortest distance from point i to point 1 in this graph.

Now you are asked to delete the m-(n-1) edge in the graph to make the graph a tree. Let disbi denote the shortest distance from point I to point 1 of the tree. Now, please find out how many edge deletion schemes there are so that for any i, there is disai=disbi.

[Input Format]

The first row contains two positive integers n and m, representing the number of points and edges of undirected connected graphs.

Next there are m lines, each line has three positive integers u,v,w, indicating that there is an undirected edge with a weight of w between point u and point v.

Data guarantees no multiple edges and self-rings.

[Output Format]

The output line is an integer, which represents the result of modularization of 214783647 by the number of schemes satisfying the conditions.

[Input sample]

3 3
1 2 2
1 3 1
2 3 1

[Output sample]

2 

[Data Scale]

analysis

It is said that there is a thing called the shortest path graph, which is a subgraph composed of the edges (u,v,w) satisfying dis(u)+w=dis(v) in the original graph.

In this question, the edge weight must be a positive integer, so the shortest path graph is a directed acyclic graph, the answer only needs to enumerate the number of spanning trees in the directed acyclic graph, but still can not pass.

In fact, in the process of constructing the shortest path map, it is to select a father for each point, and the total number of father-selectable points is the degree of this point. Obviously, the answer is the product of the degree.

The specific implementation is the shortest path, and Dijkstra is used in this capsule.

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;
priority_queue<pair<int,int> > q;
const int N=1010,M=1000100;
const long long mod=2147483647;
int n,m,head[N],ver[M],edge[M],from[M],tot,next[M],d[N],deg[N];
long long ans=1;
bool v[N];
void add(int x,int y,int z)
{
    ver[++tot]=y,edge[tot]=z,from[tot]=x,next[tot]=head[x],head[x]=tot;
}
void dijkstra()
{
    memset(d,0x7f7f7f7f,sizeof(d));
    memset(v,false,sizeof(v));
    d[1]=0;
    q.push(make_pair(0,1));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(v[x]) continue;
        v[x]=1;
        for(int i=head[x];i;i=next[i])
        {
            int y=ver[i],z=edge[i];
            if(d[y]>d[x]+z)
            {
                d[y]=d[x]+z;
                q.push(make_pair(-d[y],y));
            }
        }
    }
    for(int i=1;i<=tot;i++)
    {
        int x=from[i],y=ver[i],z=edge[i];
        if(d[x]+z==d[y]) deg[y]++;
    }
    for(int i=1;i<=n;i++)
        if(deg[i]) ans=(1LL*ans*deg[i])%mod;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);
        add(y,x,z);
    }
    dijkstra();
    cout<<ans;
    return 0;
}

T3 root number

subject

[Title Description]

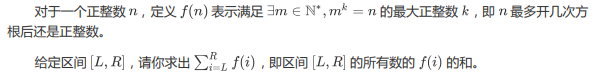
[Input Format]

The input contains multiple sets of data. Each group of data contains a row of two positive integers L,R.

The file ends with 0 (no output is required at the end).

[Output Format]

For each set of data, output a line to indicate the answer. Make sure the answer is within [0,263].

[sample input]

2 10
248832 248832
0 0

[Sample output]

13
5

[Data Scale]

analysis

Terrible Number Thesis~~~

Firstly, the interval is prefixed and expressed, so only the answer of [1,n] is needed.

It is very difficult to find the f(i) of each number i n turn. Consider the number of f(i)=k in [1,n]. The number of f(i)=k is expressed by g(k).

Using p(k) to denote the number of open k-th power or positive integers in [1,n], we can get p(k) = n1/k (downward integer).

be.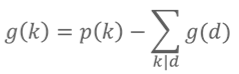

So use recursion to get the answer.

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-10;
long long l,r,f[100];
long long solve(long long x)
{
    if(x<2) return 1;
    int num=0;
    for(int i=63;i>=2;i--)
    {
        f[i]=(long long)(pow(x,(double)1.0/i)+eps)-1;
        for(int j=i+i;j<=63;j+=i) f[i]-=f[j];
        num+=f[i]*(i-1); 
    }
    return num+x;
}
int main()
{
    cin>>l>>r;
    while(l!=0&&r!=0)
    {
        cout<<solve(r)-solve(l-1)<<endl;
        cin>>l>>r;
    }
    return 0;
}

T4 travel

subject

[Title Description]

[Input Format]

The first line contains two non-negative integers n and k, meaning as described in the title description.

Next, in line n-1, there are three positive integers u,v,w in each line, indicating that there is an edge with a weight of w between u and V.

[Output Format]

Output an integer in a row to indicate the answer. Guarantee the existence of a legal solution.

[Input sample]

5 6
1 2 3
1 3 4
2 4 2
2 5 3

[Output sample]

4 

[Data Scale]

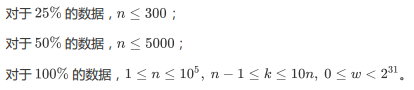
analysis

It is not difficult to find that:

• dis(u,v)=dis(u,1)+dis(v,1).
• If the number of edges passing through is odd, then one point must have an odd depth, and the other point has an even depth.

So we classify all points according to the parity of depth, and then we have two sequences a and b, which only need the k-th smallest value of ai+bi.

Code

#include <algorithm>
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;
const int N=100010;
struct node
{
    long long v;
    int p;
    node(long long a,int b):v(a),p(b){}
    bool operator < (const node &a) const
    {
        return v>a.v;
    }
};
priority_queue<node> q;
int head[N],ver[N<<1],edge[N<<1],next[N<<1],tot;
long long dis[N],deep[N],a[N],b[N],cnta,cntb;
void add(int x,int y,int z)
{
    ver[++tot]=y,edge[tot]=z,next[tot]=head[x],head[x]=tot;
}
void dfs(int x,int fa)
{
    for(int i=head[x];i;i=next[i])
    {
        int y=ver[i],z=edge[i];
        if(y==fa) continue;
        dis[y]=-dis[x]+z,deep[y]=deep[x]+1;
        dfs(y,x);
    }
}
int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n-1;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);
        add(y,x,z);
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
        if(deep[i]&1) a[++cnta]=dis[i];
        else b[++cntb]=dis[i];
    sort(b+1,b+cntb+1);
    for(int i=1;i<=cnta;i++) q.push(node(a[i]+b[1],i));
    for(int i=1;i<=cnta;i++) head[i]=1;    
    while(k>1)
    {
        node t=q.top();
        q.pop();
        if((++head[t.p])<=cntb) q.push(node(a[t.p]+b[head[t.p]],t.p));
        k--;
    }
    cout<<q.top().v;
    return 0;
}