1. Structures
Structures are important in data structures, so first understand the structure-related knowledge points.
struct LNode{ int data; char name[20]; }; //struct is the keyword that defines the structure, and LNode is the name of the structure //For example, create an object for the previous structure, struct LNode n; //Objects must be created here with the structure keyword struct.n is the object and can be used directly struct LNode{ int data; char name[20]; }n; //This creates the object n at the time of definition typedef struct LNode{ int data; struct LNode *next;//Aliases cannot be used here yet because the alias to which the code goes is undefined }node; //Typeedef is the keyword that defines the alias, and node is the alias of struct LNode.The object created is a node n; there is no need for struct LNode n; //Notice that the typedef keyword is added, followed by the node as an alias, and the node object is created at the time of definition without typedef
2. Recursion
Recursion is used a lot in tree and graph traversal. Understanding recursion is very helpful for understanding the code associated with tree diagrams.
1. Recursive implementation of 1+2+...+n.
int sum(int n){ //sum(n) is the result of returning 1+2+...+n int s; if(n == 1){ s = 1; }else{ s = sum(n-1) + n; } return s; }
Understanding the recursive function I think we should have a good grasp of the relationship between the whole and the local. The whole is what the whole recursive function does. The local is how we achieve this recursion. First of all, understand the function and its role. For example, sum(n) returns 1+2+...The first step is to consider the special case of n=1, which is the export of recursion. By the time n=1 does not recurse, it begins to return the result step by step.The second step is to call this recursive function, which combines the last step with the previous n-1 step recursive function, such as s = n+sum (n-1); sum (n-1) is the result of adding 1 to n-1. This is the function of this recursive function. Do not go into the recursion step by step, it will be dizzy. We just need to know that it is the function and we can use it directly.
2. Recursively sum any number of integers.
int sum(int a[],int n){ //A is a n integer array containing n integers, with subscripts ranging from 0 to n-1 if(n==1){//Recursive exit, when there is only one number its integer sum is a[0] return a[0]; }else{ return sum(a,n-1)+a[n-1];//sum(a,n-1) represents the sum of the first n-1 numbers in the array } }
Similar to the previous question, find out that sum(a,n) first returns the sum of the first n numbers in array a, with subscripts ranging from 0 to n-1, then determines the export n=1, and finally adds a[n-1] to the result sum(a,n-1) of the previous n-1 numbers.
3. Find the maximum of n numbers
int max(int a[],int n){//Role: Returns the maximum of n numbers if(n==1){//Recursive Exit return a[0];//Only one maximum number can be it }else{ if(a[n-1]>max(a,n-1)){//Compare the last number to the maximum of the previous n-1 numbers return a[n-1]; }else{ return max(a,n-1); } } }
4. A classic recursive question: how many ways can you walk up a 15-step staircase with a maximum of three steps in one step.
Analysis:
First, define a function, fun(n), to return to the n-step stairs, how many different walks there are;
(2) There are three ways of doing the first step:
Take one level, there are n-1 stairs left to go, and there are fun(n-1) walking styles left.
Take two steps, there are n-2 stairs left to walk, and there are fun(n-2) walking styles left.
Take the third level, there are n-3 stairs left to walk, and there are fun(n-3) walking styles left.
So the way to walk the n-step stairs is fun(n)=fun(n-1)+fun(n-2)+fun(n-3); n>3
(3) Based on the above analysis, a recursive function, fun(n), can be defined and we can quickly calculate fun(1) = 1,fun(2) = 2,fun(3) = 4. The rest can be deduced step by step through the formula.The implementation code is as follows:
int fun(int n){ //How many ways to walk back to the n-step stairs if(n==1){return 1;}//Exit if(n==2){return 2;}//Exit if(n==3){return 4;}//Exit return fun(n-1)+fun(n-2)+fun(n-3); }
The types of recursion above are similar, so is the analysis. Let's look at recursion in the tree
void PreOrder(BiTree T){ //Traversing a tree with T as its root node in order if(T!=NULL){//The exit is hidden, T==NULL does not recurse down visit(T);//The first step in sequential traversal must be to access the root node PreOrder(T->lchild);//Traversing Left Subtree PreOrder(T->rchild);//Traversing right subtree } }
These are recursive topics, and the more you do, the slower you will understand.
Chain List
The basic knowledge of chain table is not introduced much, mainly about how to do the programming problems of chain table.
In some programming problems of chain table, the first thing to do is to analyze the topic. You can draw a chain table on the draft paper. The analysis requires several pointers. Where should the initial position of the pointer point to, what role each pointer plays, how to achieve it, find out these and start the problem again.
1. For example, a simple finding and deleting all nodes with the value x from the leading node chain list L
Draw the list first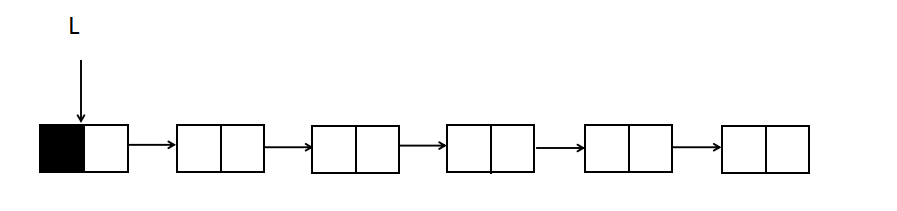
Next, analyze which pointers to use. Since finding nodes must be traversed entirely, you need a pointer P to traverse the nodes with the value x from beginning to end. The initial position of P is behind the head node, because there is no information in the head node, P should point to the first node where data is stored; when P traverses backwards from the first valid node until a node with the value x is foundHow do I delete this node?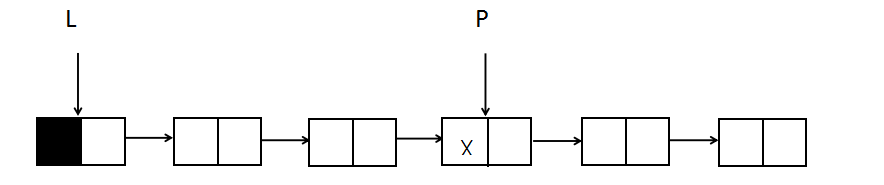
This requires another pointer, Pro, which points to the node before the P pointer, so that deletion of node X can be easily achieved, and P should always remain behind the node that Pro points to.Pro starts at the same location as L, just before the P pointer.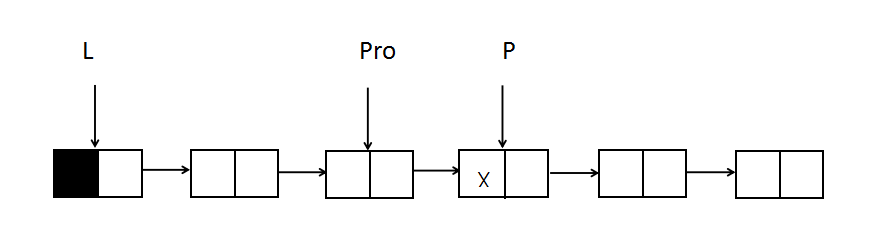
Pro->next = P->next;//Perform deletion free(P);//Release Node Space
The initial positions of the Pro and P pointers are as follows: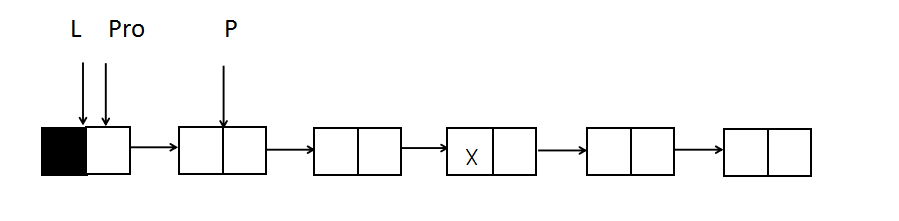
Full code:
void delete_X(LNode *L,int x){ //Delete node with value x from list L LNode *Pro,*P;//Define pointers to use Pro = L;//Define the initial location of Pro P = Pro->next;//Define the initial position of P while(P!=NULL){//P points to a node that is not empty but traverses through it all the time if(P->data == x){//Delete the node if found Pro->next = P->next; free(P); P = Pro->next;//Relocate P and continue searching }else{//Otherwise move back one bit as a whole Pro = P; p = Pro->next; } } }
2. Delete the node with the smallest median value in the single-chain list of leading nodes
First look at what pointers are needed. To find the smallest node, there must be a pointer P that keeps looking backwards, and a pointer Min that points to the smallest of these currently found nodes.Both P and min point to the first node (non-header node) at the beginning. min means that the default first node in the initial state is the minimum node. P starts from the first node and finds a smaller node than min. The min pointer has to point to the smaller node, then p continues to find it until the end of the min-specified node is the minimum node.
But how to delete it?The min node eventually points to the minimum node, and deleting it requires adding a pointer pmin in front of the min pointer, which needs to remain in front of the min pointer.The change of the Min pointer is based on the P pointer. The P pointer finds a smaller node, and the Min points directly to the node that P is currently pointing to. In this case, the P min pointer cannot be kept before the min, and a pointer Pro needs to be kept before the P.P finds the location, min goes over to p, P min goes over to pro.
The initial locations are as follows: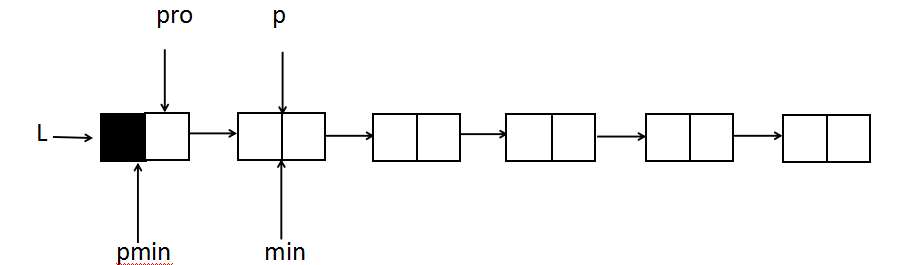
The implementation code is as follows:
void delete_min(LNode *L){ LNode *pro,*p,*pmin,*min;//Define the required pointer pro = pmin = L;//Location determination p = min = pro->next;//Location determination while(p!=NULL){//Find as long as p is not empty if(p->data<min->data){//Find a smaller node, min, pmin will pass min = p; pmin = pro; } pro = p; p = p->next; } //Min after the end refers to the smallest node, pmin before min pmin->next = min->next; free(min); }
3. Sort the L-list of the leading node chain in ascending order by direct insertion sort
Direct insertion sort considers the first number to be an ordered table, then inserts the following numbers into the ordered table in turn until all numbers are inserted into the ordered table.
The basic idea implemented in a chain table is to break the list from the first node and divide it into two chained lists, L and L2.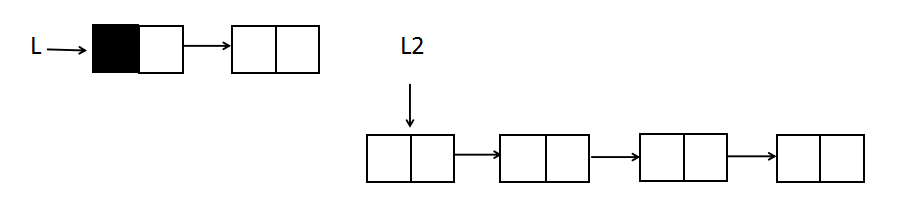
L is an ordered list with only one node. The nodes in L2 are removed and inserted into the list L to complete the sorting.
Need pointer p, P is to find the position of the node to insert in the L-chain table, ascending order must satisfy that the value of inserted node is greater than that of the p-pointer, less than that of the p-pointer to the subsequent node of the node, note that the node may be inserted at both ends, so the p-pointer should point to the head node L, because the first position may be inserted; also need pointer qro, q, QRO is to insert into the L-chain tableThe node, the first node in the L2 list, has to take out the node that QRO points to, so the pointer Q also points to the next node to insert, which is the second node in the L2 list. Otherwise, the node cannot be removed after it is removed.
The initial locations are as follows: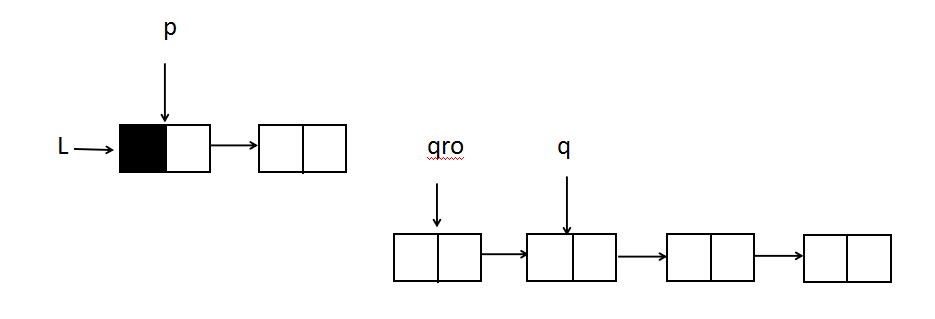
//Implementation code: void sort(LNode *L){//Use direct insertion sort for ascending sorting of chain list L LNode *p,*qro,*q;//Define Nodes p = L->next;//Define Initial Position qro = p->next;//Define Initial Position p->next = NULL;//Break the list into two chains while(qro!=NULL){//Loop insertion until qro is empty, that is, all inserted, no nodes q = qro->next;//Location defining q p = L;//p is moving, resetting its position to the beginning each time while(p->next!=NULL&&p->next->data<qro->data){//Find the location where qro is inserted, note that p->next, not p p = p->next; } qro->next = p->next; p->next = qro; qro = q;//Reset the qro position to the first node of the remaining nodes after insertion } }
IV. Trees
Tree programming problems are mainly based on tree traversal. Tree traversal includes before, after, and recursive non-recursive implementation plus hierarchical traversal of seven kinds. These traversal codes are very important, many topics can be solved by modifying the seven traversal algorithms.
1. Sequential Traversal - Recursive
void PreOrder(BiTree T){ if(T!=NULL){ visit(T);//access node PreOrder(T->lchild);//Traversing Left Subtree PreOrder(T->rchild);//Traversing right subtree } }
2. Mid-order Traversal - Recursive
void InOrder(BiTree T){ if(T!=NULL){ PreOrder(T->lchild);//Traversing Left Subtree visit(T);//access node PreOrder(T->rchild);//Traversing right subtree } }
3. Post-order Traversal - Recursive
void PostOrder(BiTree T){ if(T!=NULL){ PreOrder(T->lchild);//Traversing Left Subtree PreOrder(T->rchild);//Traversing right subtree visit(T);//access node } }
4. Sequential traversal - non-recursive
void PreOrder(BiTree T){ BiTree *p = T; SeqStack S;//Define a stack while(p||!S.Empty_Stack()){//Pointer p and stack S only need one not null to continue traversal if(P){ visit(p); S.Push_Stack(p);//p pointer stacking p = p->lchild;//Access left subtree }else{ S.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p p = p->rchild;//Access right subtree } } }
5. Ordered traversal - non-recursive
void InOrder(BiTree T){ BiTree *p = T; SeqStack S;//Define a stack while(p||!S.Empty_Stack()){//Pointer p and stack S only need one not null to continue traversal if(P){ S.Push_Stack(p);//p pointer stacking p = p->lchild;//Access left subtree }else{ S.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p visit(p); p = p->rchild;//Access right subtree } } }
6. Post-order traversal - non-recursive
void PostOrder(BiTree T){ SeqStack s1;//s1 stack holds node pointers SeqStack s2;//s2 stack stores flag, which records whether the node has been visited BiTree *p =T; int flag; while(p||!s1.Empty_Stack()){ if(p){ flag = 0; s1.Push_Stack(p);//Current p-pointer first stacked s2.Push_Stack(flag);//flag on stack, keep in sync with pointer p = p->lchild; }else{ s1.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p s2.Pop_Stack(flag);//The elements in the stack go out of the stack and assign them to flag if(flag == 0){//Indicates that the corresponding p-pointer has only entered the stack once flag = 1; s1.Push_Stack(p);//Current p-pointer second stack s2.Push_Stack(flag);//flag on stack, keep in sync with pointer p = p->rchild; }else{ visit(p); p = NULL;//p must be empty } } } }
7. Hierarchical Traversal - Queue Implementation
void LevelOrder(BiTree T){ InitQueue(Q);//Initialize Queue Q BiTree p; EnQueue(Q,T);//Root node T queued Q while(!IsEmpty(Q)){ DeQueue(Q,p);//The opposite element is queued and assigned to p visit(p); if(p->lchild!=NULL){ EnQueue(Q,p->lchild); } if(p->rchild!=NULL){ EnQueue(Q,p->rchild); } } }
The above algorithm emphasizes understanding, drawing a tree, and following the steps of the program to simulate walking down, slowly understand. It is important to note that non-recursive implementation of the tree's order and middle order, each node only once into the stack and once out of the stack, instead of recursive implementation of the tree's subsequent nodes into the stack twice, out of the stack.
Now let's do some exercises based on the traversal algorithm described above
1. Calculate the number of binary tree nodes
This is only used to count access nodes
As in recursive mode:
int count = 0; void PreOrder(BiTree T){ if(T!=NULL){ //visit(T);//access node count++;//count requires a global variable and is not affected by recursion PreOrder(T->lchild);//Traversing Left Subtree PreOrder(T->rchild);//Traversing right subtree } }
2. Calculating Binary Tree Height
The height of a binary tree is the maximum height of the left and right subtrees plus one, and the height of the left and right subtrees is the same as the height of the whole binary tree, so it can be implemented recursively
int Height(BiTree T){ if(T == NULL) return 0; else{ return Max(Height(T->lchild),Height(T->rchild))+1; } }
Tree heights can also be obtained by hierarchical traversal, which is a complex algorithm explained as follows:
Using the hierarchical traversal algorithm, set the variable level to record the number of layers where the current node is located, set the variable last to point to the rightmost node of the current layer, and compare it with the last pointer each time the hierarchy traverses out of the queue. If the two are equal, end the traversal of the current layer, add one layer, and let last point to the rightmost node of the next layer until the traversal is complete.The level value is the height of the binary tree.You can go through the process on paper as follows to gain a better understanding.Similar ideas are used when finding the number of nodes in a layer and the width of a tree.
int Btdepth(BiTree T){ if(!T){ return 0; } int front = -1,rear = -1;//Initialize Queue Head and End Pointer int last = 0,level = 0;//LastPoint to the position of the first node on the next level BiTree Q[Maxsize];//Set queue large enough to store binary tree node pointer Q[++rear] = T;//Root node enqueued BiTree p; while(front<rear){//If queue is not empty, loop p = Q[++front];//Queue if(p->lchild){ Q[++rear] = p->lchild;//Left Child Enrolled } if(p->rchild){ Q[++rear] = p->rchild;//Right Child Enrolled } if(frnot == rear){//Processing the rightmost node of this layer level++;//Layers plus one last = rear;//LastPoint Down } } return level; }
3. Access each node on the longest path in the binary tree in turn, and access the leftmost one if there are more than one.
Solve this problem with an algorithm that calculates the height of a tree, and each time we visit the highest subtree.
int Height(BiTree T){//Calculate the height of a tree whose root node is T if(T == NULL) return 0; else{ return Max(Height(T->lchild),Height(T->rchild))+1; } } void longPath(BiTree T){ if(T!=NULL){ visit(T); if(Height(T->lchild)<Height(T->rchild)){//Left subtree height is less than right subtree height longPath(T->rchild);//Recursive traversal of right subtree }else{ longPath(T->lchild);//Recursive traversal of left subtree } } }
4. Join the leaf nodes of a binary tree from left to right to form a single-chain table with the head pointer. When joining, use the right pointer field of the leaf node to store the single-chain table pointer.
The order in which we traverse leaf nodes is left to right. The relative order between them is unchanged. We can use non-recursive order and middle order to modify them slightly. We define a head er pointer and a rear Ender pointer. During traversal, each node is judged to be a leaf node (left and right subtrees are empty), and all leaf nodes are connected in sequence.Come.
BiTree *PreOrder_link(BiTree T){ BiTree *p = T,*head = NULL,*rear; SeqStack S;//Define a stack while(p||!S.Empty_Stack()){//Pointer p and stack S only need one not null to continue traversal if(P){ //visit(p); change the access P node to the following code if(p->lchild==NULL&&p->rchild == NULL){//If it is a leaf node if(head == NULL){//If it is the first leaf node head = rear = p; }else{ rear->rchild = p; rear = p; } } S.Push_Stack(p);//p pointer stacking p = p->lchild;//Access left subtree }else{ S.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p p = p->rchild;//Access right subtree } } //Finally empty the tail pointer rchild field and return the header pointer rear->rchild = NULL; return head; }
5. All ancestor nodes whose value is x are printed in the binary tree, and only one node whose value is X.
First, we need to understand that in non-recursive sequential traversal, the root node is visited last, when a node is visited, all elements in the stack are the ancestors of that node, and print out of the stack in turn.We just need to modify it on the basis of the non-recursive postorder traversal algorithm.
void PostOrder(BiTree T,int x){ SeqStack s1;//s1 stack holds node pointers SeqStack s2;//s2 stack stores flag, which records whether the node has been visited BiTree *p =T; int flag; while(p||!s1.Empty_Stack()){ if(p){ flag = 0; s1.Push_Stack(p);//Current p-pointer first stacked s2.Push_Stack(flag);//flag on stack, keep in sync with pointer p = p->lchild; }else{ s1.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p s2.Pop_Stack(flag);//The elements in the stack go out of the stack and assign them to flag if(flag == 0){//Indicates that the corresponding p-pointer has only entered the stack once flag = 1; s1.Push_Stack(p);//Current p-pointer second stack s2.Push_Stack(flag);//flag on stack, keep in sync with pointer p = p->rchild; }else{ //visit(p); modify the access node code as follows if(p->data == x){//When the value x is accessed, the elements in the stack are all ancestor nodes while(!s1.Empty_Stack()){//All elements in the print stack s1.Pop_Stack(p);//The elements in the stack go out of the stack and assign them to p visit(p); } } p = NULL;//p must be empty } } } }
This can also be derived from a more complex question, finding the closest common ancestor nodes of two nodes P and q, which is also used for the above properties. All the elements in the stack (that is, all the ancestors of p) when accessing node P are stored in one stack, and all the elements in the stack (that is, all the ancestors of q) when accessing node Q are stored in the other stack, and the result can be obtained by comparing the two stacks.
typedef struct{//Define the structure of the stack, the name of the structure after the struct can be omitted BiTree t; int flag; //The above stack for node pointers needs a corresponding flag tag stack. //In this case, if two node pointer stacks are needed, then two flag stacks are necessary. This is too cumbersome, so defining a structure for node pointers and flag tags is easy to use. }stack;//stack is a structure alias stack s[Maxsize],s1[Maxsize];//Define a stack large enough BiTree Ancestor(BiTree T,BiTree *p,BiTree *q){ int top1,top = 0;//Initialization stack pointer BiTree *bt = T; while(bt!=NULL||top>0){//Top>0 means the stack is not empty while(bt!=NULL&&bt!=p&&bt!=q){ while(bt!=NULL){ s[++top].t = bt; s[top].flag = 0; bt = bt->lchild; } } while(top!=0&&s[top].flag == 1){ //Assuming that P is to the left of q, when p is encountered, the elements in the stack are all ancestors of P if(s[top].t == p){ for(i = 1;i<=top;i++){//Transfer elements of stacks to auxiliary stacks s1 for saving s1[i] = s[i]; } top1 = top;//Save stack top position at the same time } if(s[top].t == q){ for(i = top;i>0;i--){//Match elements in two stacks for(j = top1;j>0;j--){ if(s1[j].t == s[i].t){//Same finds the closest common ancestor return s[i].t; } } } top--;//Unstack } } if(top!= 0){ s[top].flag = 1; bt = s[top].t->rchild; } } return NULL;//No return node at this point indicates no common ancestor }
Five, Fig.
The traversal algorithm of the graph is basically based on the storage structure of the adjacent table, where all the related algorithms of the graph are also based on the storage structure of the adjacent table.Graph traversal mainly includes depth-first traversal and breadth-first traversal. Depth-first traversal can be implemented by recursive and non-recursive methods.
First understand the structure of the graph
#define MaxVertexNum 100 //Maximum number of vertices in graph typedef struct ArcNode{ //Structures of Edge Table Nodes int adjvex; //Stored vertices struct ArcNode *next;//A pointer to the next arc }ArcNode; typedef struct VNode{//Structure of vertex table nodes int data;//Vertex information ArcNode *first;//A pointer to the first arc attached to that vertex }VNode; typedef struct{ VNode adjlist[MaxVertexNum];//The adjacency table is the vertex table stored sequentially int vexnum,arcnum;//Number of vertices and edges of a graph }Graph;//The structure of a graph
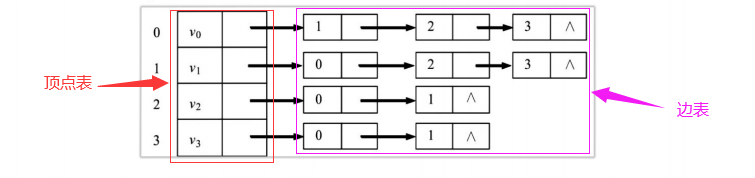
1. Width first traversal
bool visited[MaxVertexNum];//Access tag array void BFS(Graph G,int v){//Starting from vertex v, graph G is traversed with breadth first, and the algorithm relies on an auxiliary queue ArcNode *p;//Define an Edge Table Node Pointer int w; visit(v);//Access vertex v visited[v] = true;//Mark that the vertex has been visited and will not be visited again Enqueue(Q,v);//Vertex v joins the team while(!isEmpty(Q)){ Dequeue(Q,v);//Vertex v leaves the queue for(p =adjlist[v].first;p;p = p->next ){ //P is initialized as the first edge table after vertex v; P alone equals p!=NULL w = p->data; if(!visited[w]){//The vertices shown on the edge table are accessed and marked without being visited visit[w]; visited[w] = true; Enqueue(Q,w); } } } } void BFSTraverse(Graph G){ for(i= 0;i<G.vexnum;i++){ visited[i] = false;//Initialization tag array } InitQueue(Q);//Initialize secondary queue Q for(i= 0;i<G.vexnum;i++){ if(!visited[i]){ BFS(G,i); } } }
2. Depth First Traversal - Recursion
bool visited[MaxVertexNum];//Access tag array void DFS(Graph G,int v){//Starting from vertex v, graph G is traversed with depth first using recursion ArcNode *p; int w; visit(v); visited[v]=true; for(p =adjlist[v].first;p;p = p->next ){ w = p->data; if(!visited[w]){ DFS(G,w); } } } void DFSTraverse(Graph G){ for(i= 0;i<G.vexnum;i++){ visited[i] = false;//Initialization tag array } for(i= 0;i<G.vexnum;i++){ if(!visited[i]){ DFS(G,i); } } }
3. Depth-first traversal - non-recursive
bool visited[MaxVertexNum];//Access tag array void DFS_Non_RC(Graph G,int v){//Depth first traverses graph G starting from vertex v, traversing all vertices of a connected component at once ArcNode *p; int w; InitStack(S);//Initialization stack Push(S,v);//Stacking visited[v]=true; while(!IsEmpty(S)){ k = Pop(S);//Stack Out visit(k); for(p =adjlist[v].first;p;p = p->next ){ w = p->data; if(!visited[w]){ Push(S,w); visited[w] = true; } } } } void DFSTraverse(Graph G){ for(i= 0;i<G.vexnum;i++){ visited[i] = false;//Initialization tag array } for(i= 0;i<G.vexnum;i++){ if(!visited[i]){ DFS_Non_RC(G,i); } } }
Note that traversing a graph is different from traversing a graph from a vertex.If it is a connected graph, traversing the graph from a vertex can complete all the nodes at once, which means traversing the graph. If a graph has n connected components, traversing the whole graph requires traversing the graph from n vertices belonging to different connected components, that is, calling n functions traversing from a single node, such as D above.FS, BFS.
Programming questions about diagrams:
1. Use depth-first traversal and width-first traversal to determine whether there is a path from vertex V(i) to V(j) in a directed graph (i!= j).
This problem only needs to traverse the graph from a single vertex i. If vertex j appears during the traversal, the path exists, otherwise it does not exist.
//Implementation of deep traversal for(i= 0;i<G.vexnum;i++){//Initialize tag array first, not in recursion visited[i] = false; } bool DFS(Graph G,int i,int j){//Starting from vertex i, using recursive thinking, depth first traverses graph G ArcNode *p; int w; //visit(v); if(i == j){ return true; } visited[i]=true; for(p =adjlist[i].first;p;p = p->next ){ w = p->data; if(!visited[w]){ DFS(G,w,j); } } } //Implementation of breadth traversal bool BFS(Graph G,int i,int j){//Starting from vertex i, graph G is traversed with breadth first, and the algorithm relies on an auxiliary queue ArcNode *p;//Define an Edge Table Node Pointer for(i= 0;i<G.vexnum;i++){//Initialize tag array first visited[i] = false; } int w; visit(i); visited[i] = true;//Mark that the vertex has been visited and will not be visited again Enqueue(Q,i);//Vertex i enrolled while(!isEmpty(Q)){ Dequeue(Q,i);//Vertex i queued for(p =adjlist[i].first;p;p = p->next ){ //P is initialized as the first edge table after vertex v; P alone equals p!=NULL w = p->data; if(!visited[w]){//The vertices shown on the edge table are accessed and marked without being visited //visit[w]; if(w == j){//Judge here return true; } visited[w] = true; Enqueue(Q,w); } } } return false; }