Ciel and Flipboard

Problem solution

We define s ( i , j ) s(i,j) s(i,j) indicates a i , j a_{i,j} Whether the final value of ai,j is the opposite of the original value is easy to find the following properties:

• s ( i , j ) ⊗ s ( i + m , j ) ⊗ s ( m , j ) = 0 ( i < m ) s(i,j)\otimes s(i+m,j)\otimes s(m,j)=0 (i< m) s(i,j)⊗s(i+m,j)⊗s(m,j)=0(i<m)
• s ( i , j ) ⊗ s ( i , j + m ) ⊗ s ( i , m ) = 0 ( j < m ) s(i,j)\otimes s(i,j+m)\otimes s(i,m)=0 (j< m) s(i,j)⊗s(i,j+m)⊗s(i,m)=0(j<m)

Obviously, every time we operate, we must cover the second layer m m m column, our length is more than half of the whole square, and it can certainly cover the midpoint.
If the point is covered ( i , m ) (i,m) (i,m), which means that we are in i i i must cover continuous m m m points, and the total length is only 2 m − 1 2m-1 2m − 1, so ( i , j + m ) (i,j+m) (i,j+m) and ( i , j ) (i,j) There must be and only one of (i,j) is covered.
So we will certainly operate on two of them, so the XOR value must be 0 0 0.
Similarly, the part of the column is the same.

With the above properties, we can consider dividing the original square matrix into four pieces according to the central axis, which is roughly like this:

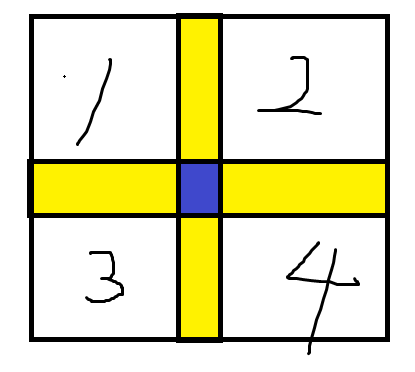
among 1 1 1， 2 2 2， 3 3 3， 4 4 All four n − 1 2 \frac{n-1}{2} 2n − 1-size square, corresponding to position s s s is equivalent or opposite, which can be determined according to the parity of points on the axis.
For a length of n n n axis, we just need to enumerate before m m m points, you can determine the values of all points on this axis.
When one axis is determined, the values of all points on the other axis are independent.
We can enumerate one axis first m m The value of m points, and then determine the point on the other axis 0 0 0 or 0 1 1 1 larger.
Point on the other axis 0 0 0 or 0 1 1 1 larger, obviously we have to take according to them 0 0 The sum of the maximum value that can be contributed at 0 is taken as 1 1 1, we can enumerate its two values to see which is greater.
When the values of the two axes are determined, the values between different points in the same block are independent, and the relationship between the corresponding points of different blocks is also determined. We only need to enumerate one point 0 0 At 0:00, four o'clock and big or big 1 1 One o'clock and four o'clock are enough.
Calculate the sum of all points on a row or column corresponding to the points on this axis and compare the size.
But at the beginning, we still need to enumerate half of the axes, but the time complexity can be seen n ⩽ 33 n\leqslant 33 n ⩽ 33 should be easy to guess.

Total time complexity O ( 2 m n 2 ) O\left(2^{m}n^2\right) O(2mn2).

Source code

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define debug(x) cerr<<#x<<"="<<x<<'\n'
typedef long long LL;
typedef unsigned long long uLL;     
const LL INF=0x3f3f3f3f3f3f3f3f;  
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int n1=50;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<LL,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){putchar('\n');while(x>9){putchar((x%10)|'0');x/=10;}putchar(x|'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
int n,m;LL ans,a[35][35];
bool rev[35];
void work(){
	LL res=0;res+=(rev[m]?-a[m][m]:a[m][m]);
	for(int i=1;i<m;i++)
		res+=(rev[i]?-a[i][m]:a[i][m]),
		res+=((rev[i]^rev[m])?-a[i+m][m]:a[i+m][m]);
	for(int i=1;i<m;i++){
		LL sum1=a[m][i]+(rev[m]?-a[m][i+m]:a[m][i+m]);
		for(int j=1;j<m;j++)
			if(rev[j]){
				if(rev[m])sum1+=Fabs(a[j][i]-a[j][i+m]+a[j+m][i]+a[j+m][i+m]);
				else sum1+=Fabs(a[j][i]-a[j][i+m]+a[j+m][i]-a[j+m][i+m]);
			}
			else{
				if(rev[m])sum1+=Fabs(a[j][i]+a[j][i+m]+a[j+m][i]-a[j+m][i+m]);
				else sum1+=Fabs(a[j][i]+a[j][i+m]+a[j+m][i]+a[j+m][i+m]);
			}
		LL sum2=-a[m][i]+(rev[m]?a[m][i+m]:-a[m][i+m]);
		for(int j=1;j<m;j++)
			if(rev[j]){
				if(rev[m])sum2+=Fabs(a[j][i]-a[j][i+m]-a[j+m][i]-a[j+m][i+m]);
				else sum2+=Fabs(a[j][i]-a[j][i+m]-a[j+m][i]+a[j+m][i+m]);
			}
			else{
				if(rev[m])sum2+=Fabs(a[j][i]+a[j][i+m]-a[j+m][i]+a[j+m][i+m]);
				else sum2+=Fabs(a[j][i]+a[j][i+m]-a[j+m][i]-a[j+m][i+m]);
			} 
		res+=max(sum1,sum2);
	}
	ans=max(ans,res);
}
void dosaka(int id){
	if(id>m){work();return ;}
	rev[id]=1;dosaka(id+1);rev[id]=0;dosaka(id+1);
}
signed main(){
	read(n);m=(n+1)/2;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			read(a[i][j]);
	dosaka(1);
	printf("%lld\n",ans);
	return 0;
}

thank you!!!