First, it's easy to know b b b sequence in a a The order in a must be sorted from small to large, otherwise exchange b b b in reverse order will be better.

Then there is a very ghost conclusion.

set up p i p_i pi indicates that only b i b_i bi} insert a a In a sequence, the optimal position is inserted in a p i − 1 a_{p_i-1} api − 1 − and a p i a_{p_i} api ， note that for the same i i i， p i p_i pi # there may be more than one.

Conclusion: if b j < b i b_j<b_i bj < Bi, for multiple p j p_j Any one of pj ， exists p i p_i pi makes p j ≤ p i p_j\leq p_i pj​≤pi​.

prove:

First consider how to obtain the "optimal position" b j b_j bj, let's put a a Less than in a b j b_j The number of bj + 0 0 0, greater than b j b_j The number of bj + 1 1 1, then insert b j b_j bj} position at p j p_j pj's contribution is a 1 , ⋯   , a p j − 1 a_1,\cdots,a_{p_j-1} a1,..., apj − 1 1 1 Number of 1 plus a p j , ⋯   , a n a_{p_j},\cdots,a_n apj,..., an 0 0 Number of 0.

Here, in order to prove the intuition, we do not consider it a a There are and in a b j b_j In the case of bj ＾ equal numbers, the proof method considering this case is the same.

Consider the counter evidence method and assume p i < p j p_i<p_j pi < PJ, put the sequence a a a divided into three sections: A = [ 1 , p i − 1 ] A=[1,p_i-1] A=[1,pi​−1]， B = [ p i , p j − 1 ] B=[p_i,p_j-1] B=[pi​,pj​−1]， C = [ p j , n ] C=[p_j,n] C=[pj​,n].

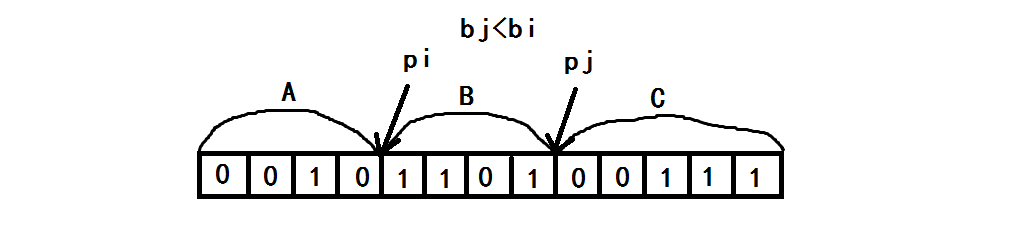
Note from b j b_j bj becomes b i b_i After the test, a a a in the sequence, only 1 1 1 becomes 0 0 0.

set up A 0 , A 1 A_0,A_1 A0, A1 indicates A A Original in A 0 , 1 0,1 Number of 0,1, A 0 ′ , A 1 ′ A'_0,A'_1 A0 ', A1' indicates from b j b_j bj becomes b i b_i bi # rear A A A medium 0 , 1 0,1 Number of 0,1. B , C B,C B. C similarly defined.

that p j p_j pj's contribution is: A 1 + B 1 + C 0 A_1+B_1+C_0 A1​+B1​+C0​.

because p j p_j pj# yes b j b_j The optimal position of bj ， so we can put p j p_j pj becomes p i p_i pi ， will not be in a better position, so: ( A 1 + B 1 + C 0 ) − ( A 1 + B 0 + C 0 ) ≤ 0 (A_1+B_1+C_0)-(A_1+B_0+C_0)\leq 0 (A1 + B1 + C0) − (A1 + B0 + C0) ≤ 0, i.e B 1 − B 0 ≤ 0 B_1-B_0\leq 0 B1​−B0​≤0.

p i p_i pi's contribution is: A 1 ′ + B 0 ′ + C 0 ′ A_1'+B_0'+C_0' A1′​+B0′​+C0′​.

Ruoba p i p_i pi ， adjust to p j p_j pj# location, contribution: A 1 ′ + B 1 ′ + C 0 ′ A_1'+B_1'+C_0' A1 ′ + B1 ′ + C0 ′ is obtained by subtracting the contribution before adjustment ( A 1 ′ + B 1 ′ + C 0 ′ ) − ( A 1 ′ + B 0 ′ + C 0 ′ ) = B 1 ′ − B 0 ′ (A_1'+B_1'+C_0')-(A_1'+B_0'+C_0')=B_1'-B_0' (A1 ′ + B1 ′ + C0 ′) − (A1 ′ + B0 ′ + C0 ′) = B1 ′− B0 ′, and B 1 ′ − B 0 ′ ≤ B 1 − B 0 ≤ 0 B_1'-B_0'\leq B_1-B_0\leq 0 B1 ′− B0 ′≤ B1 − B0 ≤ 0, so p i p_i pi ， adjust to p j p_j pj# must be in a good position, so it must exist p i ≥ p j p_i\geq p_j pi​≥pj​.

Then we can for each b i b_i bi# plug it directly into the p i p_i According to this conclusion, such interpolation must also meet the requirements b i b_i bi# sorted from small to large.

More precisely, this interpolation first ensures b b b and a a The reverse order pairs between a are the least, and it can be seen from the conclusion that at this time b b b and b b The reverse order pair between b is 0 0 0, also takes the lower bound, and a a a and a a The reverse order pair between a is fixed.

The question now is how to find each value quickly b i b_i The optimal position of bi ＾ and its reverse order contribution to.

Using segment tree maintenance [ 1 , i − 1 ] [1,i-1] In [1,i − 1] 1 1 Number of 1+ [ i , n ] [i,n] In [i,n] 0 0 The minimum number of 0.

#include<bits/stdc++.h>

#define N 1000010
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
#define mk(a,b) make_pair(a,b)

using namespace std;

inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^'0');
		ch=getchar();
	}
	return x*f;
}

int T,n,m,nn,a[N],b[N],bb[N<<1];

namespace AA
{
	int c[N<<1],lowbit[N<<1];
	void init()
	{
		const int t=2000000;
		for(int i=1;i<=t;i++) lowbit[i]=(i&-i);
	}
	void add(int x,int y)
	{
		for(;x<=nn;x+=lowbit[x]) c[x]+=y;
	}
	int query(int x)
	{
		int ans=0;
		for(;x;x-=lowbit[x]) ans+=c[x];
		return ans;
	}
	ll work()
	{
		for(int i=1;i<=nn;i++) c[i]=0;
		ll ans=0;
		for(int i=n;i>=1;i--)
		{
			ans+=query(a[i]-1);
			add(a[i],1);
		}
		return ans;
	}
}

namespace BA
{
	int minn[N<<2],lazy[N<<2];
	void downn(int k,int v)
	{
		minn[k]+=v,lazy[k]+=v;
	}
	void down(int k)
	{
		if(lazy[k])
		{
			downn(k<<1,lazy[k]);
			downn(k<<1|1,lazy[k]);
			lazy[k]=0;
		}
	}
	void up(int k)
	{
		minn[k]=min(minn[k<<1],minn[k<<1|1]);
	}
	void build(int k,int l,int r)
	{
		lazy[k]=0;
		if(l==r)
		{
			minn[k]=l-1;
			return;
		}
		int mid=(l+r)>>1;
		build(k<<1,l,mid);
		build(k<<1|1,mid+1,r);
		up(k);
	}
	void update(int k,int l,int r,int ql,int qr,int v)
	{
		if(ql<=l&&r<=qr)
		{
			downn(k,v);
			return;
		}
		down(k);
		int mid=(l+r)>>1;
		if(ql<=mid) update(k<<1,l,mid,ql,qr,v);
		if(qr>mid) update(k<<1|1,mid+1,r,ql,qr,v);
		up(k);
	}
	pii p[N];
	ll work()
	{
		for(int i=1;i<=n;i++)
			p[i]=mk(a[i],i);
		sort(p+1,p+n+1);
		sort(b+1,b+m+1);
		build(1,1,n+1);
		ll ans=0;
		int tmp1=1,tmp2=1;
		for(int i=1;i<=m;i++)
		{
			while(tmp2<=n&&p[tmp2].fi<=b[i])
			{
				update(1,1,n+1,p[tmp2].se+1,n+1,-1);
				tmp2++;
			}
			while(tmp1<=n&&p[tmp1].fi<b[i])
			{
				update(1,1,n+1,1,p[tmp1].se,1);
				tmp1++;
			}
			ans+=minn[1];
		}
		return ans;
	}
}

int main()
{
	AA::init();
	T=read();
	while(T--)
	{
		n=read(),m=read();
		for(int i=1;i<=n;i++) bb[i]=a[i]=read();
		for(int i=1;i<=m;i++) bb[n+i]=b[i]=read();
		sort(bb+1,bb+n+m+1);
		nn=unique(bb+1,bb+n+m+1)-bb-1;
		for(int i=1;i<=n;i++) a[i]=lower_bound(bb+1,bb+nn+1,a[i])-bb;
		for(int i=1;i<=m;i++) b[i]=lower_bound(bb+1,bb+nn+1,b[i])-bb;
		printf("%lld\n",AA::work()+BA::work());
	}
	return 0;
}