1. 2D pose optimization_ graph_ 2d.cc

1.1. Problem description

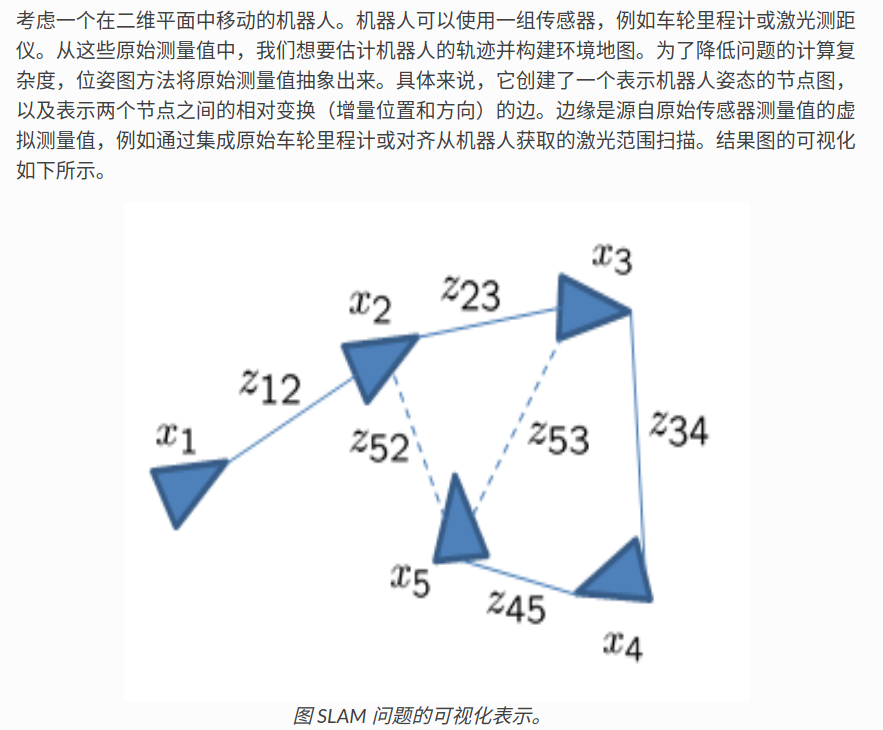
be careful:

1. There is no problem with the official website tutorial in the above picture! Because the tutorial on the official website is really very careful! Note that the formula is Ra^T, and Ra is indeed the rotation matrix from the node coordinate system to the world coordinate system, but because Pb PA is the position representation under the world coordinate system, and hat_pab represents the position and attitude of b relative to a in the coordinate system of a, so it is necessary to convert them all to the coordinate system of a for subtraction. Since the rotation matrix is an orthogonal matrix, that is, the inverse of R is equal to the transpose of R. Therefore, the above formula uses the transpose of R, that is, the inverse of R, that is, the transformation relationship between the world coordinate system and the robot coordinate system, and then multiplied by Pb PA (expressed in the world coordinate system), the result is expressed in the coordinate system of a!
2. In the bottom line, local parameterization is used, and then there is a Normalize. Later, combined with the program, it is found that the meaning is as follows: since the rotation angle is a periodic value, it should be defined in a monotonic interval, so it is selected here [- pi, pi) this interval, and then this local parameterization operation is equivalent to adding constraints to the rotation angle, so that the updated results (that is, the ψ+δψ) Keep it within this range. The function in the official website tutorial is a class defined by themselves, which is not defined in the ceres library. However, a LocalParameterization class is defined in the ceres library. Its purpose should be the same as here, in order to make some constraints on variables during variable optimization.

1.2. Detailed procedure

1.2.1.pose_graph_2d_error_term.h

This file mainly implements the classes required by ceres to calculate the residuals, that is, the structures or classes that contain the template () operator previously defined. In the definition of this class, the official notes explain the calculation formula of the residuals in great detail, which is easy to understand in combination with the program on the official website.

// Computes the error term for two poses that have a relative pose measurement
// between them. Let the hat variables be the measurement.
//
// residual =  information^{1/2} * [  r_a^T * (p_b - p_a) - \hat{p_ab}   ]
//                                 [ Normalize(yaw_b - yaw_a - \hat{yaw_ab}) ]
//
// where r_a is the rotation matrix that rotates a vector represented in frame A
// into the global frame, and Normalize(*) ensures the angles are in the range
// [-pi, pi).
class PoseGraph2dErrorTerm {
 public:
  PoseGraph2dErrorTerm(double x_ab,   // These are the actual observations, that is, the edges in the pose map
                       double y_ab,
                       double yaw_ab_radians,
                       const Eigen::Matrix3d& sqrt_information)
      : p_ab_(x_ab, y_ab),
        yaw_ab_radians_(yaw_ab_radians),
        sqrt_information_(sqrt_information) {}

  template <typename T>
   // The values of nodes are passed in the bracket operator, and then these values are used to calculate the estimated observations,
   // Make a difference with the actual incoming observation value to obtain the residual
  bool operator()(const T* const x_a,  
                  const T* const y_a,
                  const T* const yaw_a,
                  const T* const x_b,
                  const T* const y_b,
                  const T* const yaw_b,
                  T* residuals_ptr) const {
    const Eigen::Matrix<T, 2, 1> p_a(*x_a, *y_a);
    const Eigen::Matrix<T, 2, 1> p_b(*x_b, *y_b);

    // Why should it be declared as a Map? It is often operated, and the data assigned to it is the data type of Eigen?
    // map is like an array in C + +, mainly to interact with native C + + arrays
    Eigen::Map<Eigen::Matrix<T, 3, 1>> residuals_map(residuals_ptr);  

    residuals_map.template head<2>() =
        RotationMatrix2D(*yaw_a).transpose() * (p_b - p_a) - p_ab_.cast<T>();
    residuals_map(2) = ceres::examples::NormalizeAngle(
        (*yaw_b - *yaw_a) - static_cast<T>(yaw_ab_radians_));

    // Scale the residuals by the square root information matrix to account for
    // the measurement uncertainty.
    residuals_map = sqrt_information_.template cast<T>() * residuals_map;

    return true;
  }

  // When I see static again, I just want to improve the compactness of the program, because the following function is only used for the current class, which is similar to a global function
  static ceres::CostFunction* Create(double x_ab,
                                     double y_ab,
                                     double yaw_ab_radians,
                                     const Eigen::Matrix3d& sqrt_information) {
    return (new ceres::
                AutoDiffCostFunction<PoseGraph2dErrorTerm, 3, 1, 1, 1, 1, 1, 1>(
                    new PoseGraph2dErrorTerm(
                        x_ab, y_ab, yaw_ab_radians, sqrt_information)));
  }

  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

 private:
  // The position of B relative to A in the A frame.
  const Eigen::Vector2d p_ab_;
  // The orientation of frame B relative to frame A.
  const double yaw_ab_radians_;
  // The inverse square root of the measurement covariance matrix.
  const Eigen::Matrix3d sqrt_information_;
};

Pay attention to several details in the above procedure:

1. It's the same as the original routine. The formal parameters of the class pass in the actually observed data points, that is, the edges in g2o. These data values will be assigned to the member variables of the class. These member variables, that is, the observed data values, will be used when calculating the residuals in the () operation Operator, which passes in the value of the vertex, that is, the vertex in g2o, or the value to be optimized. Then, in the () operation, the calculated observation value is obtained by using these vertex values, and then subtracted from the actual observation value to obtain the residual.

2. The static function appears again in this class, which is a pointer to the automatic derivation object returned by new. The advantage of writing in this class is to make the program more compact, because the construction parameters in the automatic derivation object are closely related to the class data we define.

3. When defining residuals in () operation, the map class in eigen is used. In fact, the map class is to be compatible with eigen's matrix operation and C + + array operation.
   (1) In the program, there is a sentence EIGEN_MAKE_ALIGNED_OPERATOR_NEW that declares memory alignment, which is necessary when using Eigen data type in custom classes. In other cases, you can see that Eigen:: align... Is added after inserting Eigen variable in std::vector, which is also to declare Eigen memory alignment, so that STL container can be used. Therefore, it should be clear that Eigen is for implementation Now, the memory allocation of matrix operation is different from that of native C + +, which needs to be declared many times.
   (2) Returning to the map class, this class is designed to implement the same memory allocation method as arrays in C + +. For example, it can be accessed quickly by using pointers; but at the same time, it can support eigen's matrix operation, so it is a good choice to declare it as a map class when matrix elements need to be operated or accessed frequently. Let's see why it should be declared as a map class here? First Operation, the calculated residuals should be stored in this matrix; secondly, the calculated results (= right) are all the data types of eigen, so they should also be compatible with the data types of eigen. Therefore, it meets the two cases of using map, so it is very suitable to use map class.
   (3) For details, see: What exactly does the Map class in the Eigen library do
   (4) Question: when assigning values, what is the usage of template in map.template?

residuals_map.template head<2>() =
        RotationMatrix2D(*yaw_a).transpose() * (p_b - p_a) - p_ab_.cast<T>();
    residuals_map(2) = ceres::examples::NormalizeAngle(
        (*yaw_b - *yaw_a) - static_cast<T>(yaw_ab_radians_));

1.2.2.pose_graph_2d.h

This file is the main file, which is mainly used to add residual blocks. For each observation data, residual blocks need to be added. Then, there is the problem of normalizing the range of rotation angle mentioned on the official website.

Secondly, there is another important problem, that is, the initial pose is set to a constant at the end of the program, and it is not optimized, that is, the long annotation explains it. I don't understand it very well.

// The pose graph optimization problem has three DOFs that are not fully
// constrained. This is typically referred to as gauge freedom. You can apply
// a rigid body transformation to all the nodes and the optimization problem
// will still have the exact same cost. The Levenberg-Marquardt algorithm has
// internal damping which mitigate this issue, but it is better to properly
// constrain the gauge freedom. This can be done by setting one of the poses
// as constant so the optimizer cannot change it.
The pose graph optimization problem has three incompletely constrained degrees of freedom. This is commonly referred to as normal degrees of freedom. You can apply rigid body transformation to all nodes, and the optimization problem still has exactly the same cost. The Levenberg Marquardt algorithm has internal damping to alleviate this problem, but it is best to constrain the normal degrees of freedom appropriately. This can be achieved by setting one of the poses to constant Quantity so that the optimizer cannot change it.

// Constructs the nonlinear least squares optimization problem from the pose
// graph constraints.
// Constraint2d is a custom structure class that describes the pose constraints between vertices, that is, the edges in g2o
void BuildOptimizationProblem(const std::vector<Constraint2d>& constraints,
                              std::map<int, Pose2d>* poses,
                              ceres::Problem* problem) {
  CHECK(poses != NULL);
  CHECK(problem != NULL);
  if (constraints.empty()) {
    LOG(INFO) << "No constraints, no problem to optimize.";
    return;
  }
  // LossFunction is the sum function. Kernel function is not used here
  ceres::LossFunction* loss_function = NULL;
  // Local parameterization:
  // Lastly, we use a local parameterization to normalize the orientation in the range which is normalized between[-pi,pi)
  ceres::LocalParameterization* angle_local_parameterization =
      AngleLocalParameterization::Create();

  // Use a constant iterator to access the container and get all the elements in the container
  for (std::vector<Constraint2d>::const_iterator constraints_iter =
           constraints.begin();
       constraints_iter != constraints.end();
       ++constraints_iter) {
    const Constraint2d& constraint = *constraints_iter;  // Gets the constraint element currently accessed

    std::map<int, Pose2d>::iterator pose_begin_iter =
        poses->find(constraint.id_begin);  // The iterator pointing to vertex 1 is obtained according to the vertex Id number of the constraint
    CHECK(pose_begin_iter != poses->end())  // eureka
        << "Pose with ID: " << constraint.id_begin << " not found.";
    std::map<int, Pose2d>::iterator pose_end_iter = // The iterator pointing to vertex 2 is obtained according to the vertex Id number of the constraint
        poses->find(constraint.id_end);
    CHECK(pose_end_iter != poses->end())
        << "Pose with ID: " << constraint.id_end << " not found.";

    const Eigen::Matrix3d sqrt_information =
            // llt = LL^T, cholesky decomposition, and then matrixL is the matrix composed of cholesky factors
        constraint.information.llt().matrixL();  // The information matrix is the inverse of the covariance matrix
    // Ceres will take ownership of the pointer.
    // PoseGraph2dErrorTerm is a specially defined class for 2D pose graph optimization, which is equivalent to the () operator with residual block defined in this class
    // It is the same as the structure or class used to calculate the residual. costfunction must be used when adding parameter blocks
    ceres::CostFunction* cost_function = PoseGraph2dErrorTerm::Create(
        constraint.x, constraint.y, constraint.yaw_radians, sqrt_information);
    // For each observation, a residual block is added
    problem->AddResidualBlock(cost_function,
                              loss_function,
                              &pose_begin_iter->second.x,  // Because this is a map iterator, first in the map is the key value, and second is the value value
                              &pose_begin_iter->second.y,  // Because the key stores the id number of the pose, the pose of the vertex is used here, so it is the value
                              &pose_begin_iter->second.yaw_radians,
                              &pose_end_iter->second.x,
                              &pose_end_iter->second.y,
                              &pose_end_iter->second.yaw_radians);

    // Set parameterization, where the rotation angle of the pose of the two vertices of the edge is set to local_parameterization
    problem->SetParameterization(&pose_begin_iter->second.yaw_radians,
                                 angle_local_parameterization);
    problem->SetParameterization(&pose_end_iter->second.yaw_radians,
                                 angle_local_parameterization);
  }

  // The pose graph optimization problem has three DOFs that are not fully
  // constrained. This is typically referred to as gauge freedom. You can apply
  // a rigid body transformation to all the nodes and the optimization problem
  // will still have the exact same cost. The Levenberg-Marquardt algorithm has
  // internal damping which mitigate this issue, but it is better to properly
  // constrain the gauge freedom. This can be done by setting one of the poses
  // as constant so the optimizer cannot change it.
  std::map<int, Pose2d>::iterator pose_start_iter = poses->begin();
  CHECK(pose_start_iter != poses->end()) << "There are no poses.";
  problem->SetParameterBlockConstant(&pose_start_iter->second.x);
  problem->SetParameterBlockConstant(&pose_start_iter->second.y);
  problem->SetParameterBlockConstant(&pose_start_iter->second.yaw_radians);
}