Title Description
A1,A2,⋯,An It's a n An array of natural numbers (non negative integers). We call it Ai,⋯,Aj Is a non-zero segment if and only if the following conditions are met at the same time:
- 1≤i≤j≤n；
- For any integer k. If i ≤ K ≤ j, then Ak>0；
- i=1 or Ai−1=0；
- j=n or Aj+1=0.
Here are some simple examples:
- A=[3,1,2,0,0,2,0,4,5,0,2] Medium four The non-zero segments are [3,1,2],[2],[4,5] and [2]；
- A=[2,3,1,4,5] have only one A non-zero segment;
- A=[0,0,0] Then there are no non-zero segments (i.e. the number of non-zero segments is) 0).
Now we can compare arrays A Do the following: select any positive integer p. Then A All less than p All the numbers become 0 Try to choose a suitable one p. Make array A The number of non-zero segments in reaches the maximum. If entered A The number of non-zero segments has reached the maximum, which can be taken p=1, i.e. No A Make any changes.
Input format
Read in data from standard input.
The first line of input contains a positive integer n.
The second line of input contains n A natural number separated by spaces A1,A2,⋯,An.
Output format
Output to standard output.
Only one integer is output to represent the array A The maximum number of non-zero segments after operation.
Example 1 input
11 3 1 2 0 0 2 0 4 5 0 2
Sample 1 output
5
Example 1 explanation
p=2 When, A=[3,0,2,0,0,2,0,4,5,0,2], 5 The non-zero segments are [3],[2],[2],[4,5] and [2]； At this time, the number of non-zero segments reaches the maximum.
Example 2 Input
14 5 1 20 10 10 10 10 15 10 20 1 5 10 15
Example 2 output
4
Example 2 explanation
p=12 When, a = [0,0,20,0,0,0,15,0,20,0,0,0,0,15], 4 The non-zero segments are [20],[15],[20] and [15]； At this time, the number of non-zero segments reaches the maximum.
Example 3 input
3 1 0 0
Example 3 output
1
Example 3 explanation
p=1 When, A=[1,0,0], only one Non zero segments [1] , the number of non-zero segments reaches the maximum.
Example 4 input
3 0 0 0
Example 4 output
0
Data
Example 4 explanation
whether p What is the value, A None of them contain non-zero segments, so the number of non-zero segments is at most 0
Subtask
70% The test data meet the requirements n≤1000；
All test data meet n≤5 ×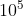
, and array A No more than 
.
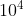problem analysis
70 code points (recursion + violence)
At the first glance, I saw the supplement of the problem scale. After simple calculation, I realized that it was impossible to use simulated violence to solve the problem, so I ran for 70 points at the beginning. I felt good before looking for P, and then... In short, the idea of 70 points is to recursively calculate the number of non-zero segments of a given sequence according to the meaning of the problem, and then violence every possible p value, Record and update max.
#include<iostream>
using namespace std;
int const N = 1000;
int a[N];
int feilingduan(int s,int e,int p){
if(s == e ){
if(a[s] - p < 0)
return 0;
else{
return 1;
}
}else{
int mid = (s + e)/2;
if(a[mid] - p >= 0 && a[mid+1] - p >= 0){
return feilingduan(s,mid,p) + feilingduan(mid+1,e,p) - 1;
}else{
return feilingduan(s,mid,p) + feilingduan(mid+1,e,p);
}
}
}
int main(){
int n;
cin >> n;
int maxa = 0;
for(int i = 0;i < n;i++){
cin>>a[i];
if(a[i] > maxa){
maxa = a[i];
}
}
int p = 1;
int max = 0;
for(p = 1;p <= maxa;p++ ){
if(max < feilingduan(0,n-1,p) ){
max = feilingduan(0,n-1,p);
}
}
cout<<max;
}
/*
110 + 022 l + r
111 + 022 l + r
110 + 200 l + r
111 + 222 l + r - 1
*/100 point code (recursion + violence + three points)
The next step is the optimization on this basis. At first, I directly thought of the idea similar to dichotomy. Later, after thinking, I found that it could not be realized, because it was neither monotonous nor unipolar. I read it later Teacher's solution Only then did I know that there were three optimization ideas (although the teacher said it was lucky, it was still 100).
#include<iostream>//42min
using namespace std;
int const N = 5*100000;
int a[N];
int n;
int feilingduan(int s,int e,int p){
if(s == e ){
if(a[s] - p < 0)
return 0;
else{
return 1;
}
}else{
int mid = (s + e)/2;
if(a[mid] - p >= 0 && a[mid+1] - p >= 0){
return feilingduan(s,mid,p) + feilingduan(mid+1,e,p) - 1;
}else{
return feilingduan(s,mid,p) + feilingduan(mid+1,e,p);
}
}
}
int findmax(int sp,int ep){
while(ep - sp > 4){
int ssp = sp + (ep - sp + 1) / 3;
int eep = ep - (ep - sp + 1) / 3;
if(feilingduan(0,n-1,ssp) < feilingduan(0,n-1,eep))
sp = ssp;
else
ep = eep;
}
int max = 0;
for(int i = sp;i <= ep ;i++ ){
if(max < feilingduan(0,n-1,i) ){
max = feilingduan(0,n-1,i);
}
}
return max;
}
int main(){
cin >> n;
int maxa = 0;
for(int i = 0;i < n;i++){
cin>>a[i];
if(a[i] > maxa){
maxa = a[i];
}
}
if(n <= 1000){
int p = 1;
int max = 0;
for(p = 1;p <= maxa;p++ ){
if(max < feilingduan(0,n-1,p) ){
max = feilingduan(0,n-1,p);
}
}
cout<<max;
}
else{
cout<<findmax(1,maxa);
}
}
/*
110 + 022 l + r
111 + 022 l + r
110 + 200 l + r
111 + 222 l + r - 1
*/100 point code (index)
According to the teacher's problem solution, I learned the teacher's index code. However, I feel that it is easy to confuse whether the book array storage is set to 0 and 1 is set to 0, so I changed it and used the array to represent its outline. For example, 1 is non-0 and 0 is < p, but the conditions for changing the segmentation have not changed.
#include<iostream>//42min + 30min
#include<vector>
using namespace std;
int const N = 5*100000;
int a[N];//Store each specific data
int range[N];//Stored as abstract 0 1 0 represents < p 1 represents > = P
vector<int>v[10000+1];//Each v[i] stores the position corresponding to all I
int main(){
int n;
int last = 1;//Last is the score of the last stroke. When p = 0, last = 1
cin >> n;
int maxa = 0;
for(int i = 1;i <= n;i++){
cin >> a[i];
v[a[i]].push_back(i);
if(a[i] > maxa){
maxa = a[i];
}
range[i] = 1;
}
range[0] = 0;
range[n + 1] = 0;
int max = 0;
for(int p = 0;p <= maxa;p++){
if(v[p].size() != 0){//Mark the number less than p as 0 in the range array, which is equivalent to changing the condition to < = p to 1. If the problem is not investigated, p has little impact
int t = last;
for(int i = 0;i < v[p].size();i++){
range[ v[p][i] ]= 0;//Set all in v[p] to 0
if(range[ v[p][i] - 1] == 0 && range[ v[p][i] + 1] == 0){
t--;
}else if(range[ v[p][i] - 1] == 1 && range[ v[p][i] + 1] == 1){
t++;
}
}
if(max < last) max = last;
if(max < t) max = t;
last = t;
}
}
cout<<max;
}
/*
110 + 022 l + r
111 + 022 l + r
110 + 200 l + r
111 + 222 l + r - 1
*/
/*
01111110 p = 0
01010110 p = 1
*/