In C language, we all know about stack and queue.
C + + provides a better solution. STL can help developers reduce a lot of work. In other words, some big guys have helped us write these data structures and encapsulated them into a library. For these basic data structures, you can create a data structure object like using int and double.
stack simulation
Introducing stack
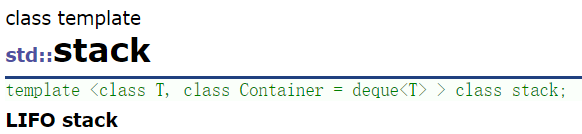
Compared with the "official" description of stack, STL basically implements a class template, which allows users to create different types of data structures according to their own needs.

It is described here that stack is a container adapter. In other words, stack is not a pure container. Unlike vector, it implements a sequence table by itself. Instead, it adapts to other lower level containers and makes some modifications.
In other words, stack uses other containers, such as vector and list, to make relevant adjustments to simulate the effect of a stack.
Specifically, use class container = deque < T > to adapt the deque container.
Class method
Look at stack's class methods

As a last in first out data structure, stack can operate only the top elements of the stack, and other elements cannot operate.
Simulate the basic functions of a stack
namespace cz
{
template <class T,class Container=std::vector<T>>
class stack
{
public:
stack()
:con(T())
{}
void pop(void)
{
con.pop_back();
}
void push(const T& val)
{
con.push_back(val);
}
size_t size(void)
{
return con.size();
}
T top(void)
{
return con.back();
}
bool empty(void)
{
return con.empty();
}
private:
Container con;
};
}
This is a basic class template implemented in my namespace. I use stack to adapt vector, which is equivalent to using sequence table to implement a stack.
The spring stack uses vector::pop_back()
The stack uses vector::push_back()
All operate on the last element of the sequence table.
Reference questions
Leetcode-946. Verify stack sequence
queue

Like stack, it is also used as a container adapter.

Class method of queue

Simulation Implementation
namespace cz
{
template <class T,class Container=std::vector<T>>
class queue
{
public:
size_t size(void)
{
return _con.size();
}
void pop(void)
{
_con.erase(_con.begin());
}
void push(const T& val)
{
_con.push_back(val);
}
bool empty(void)
{
return _con.empty();
}
T front(void)
{
return _con.front();
}
T back(void)
{
return _con.back();
}
private:
Container _con;
};
}
For queue outgoing, you can use ear and iterator begin to erase.
priority_queue
Priority queue
Although it is a queue, in fact, it is a heap (a special binary tree). Moreover, it is also a container adapter.
This is similar to the heap. Elements can be inserted at any time, and only the largest / smallest heap elements (at the top of the priority queue) can be retrieved.

The priority queue is the adapter of vector, because the heap is basically arranged through an array.
functor
This class compare = less < typename container:: value_type >
In fact, it is an imitation function, and less is actually a class.
Imitation function is to simulate the effect of function through class.
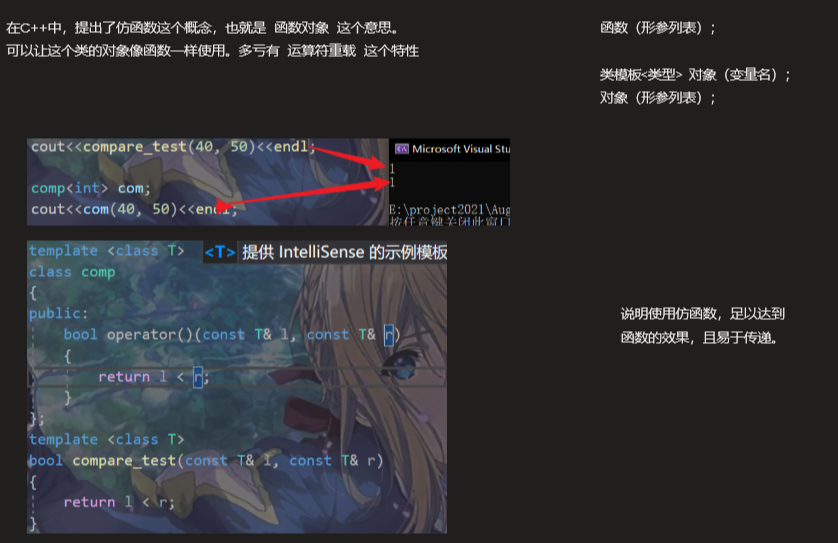

The instantiation type of the imitative function here is the element type of the adapted container, which plays a comparative role.
Because when creating a large / small heap, it is necessary to compare the child node with the parent node. The exchange will be carried out only when the conditions are met. In addition, whether to build a large heap or a small heap can be controlled through less < >, greater < >. Less can build a large heap and greater can build a small heap.
Simulation Implementation
namespace cz
{
template<class T,class Container=std::vector<T>,class Compare=std::less<typename Container::value_type> >
class priority_queue
{
public:
priority_queue(const Compare& comp = Compare(),const Container& ctnr = Container())//structure
:_con(ctnr)//Container construction
,comp(comp)//Imitative function construction
{}
template <class InputIterator>//iterator
priority_queue(InputIterator first, InputIterator last,
const Compare& comp = Compare(),
const Container& ctnr = Container())
: _con(ctnr)//Container construction
, comp(comp)//Imitative function construction
{
//Iterator deep copy
}
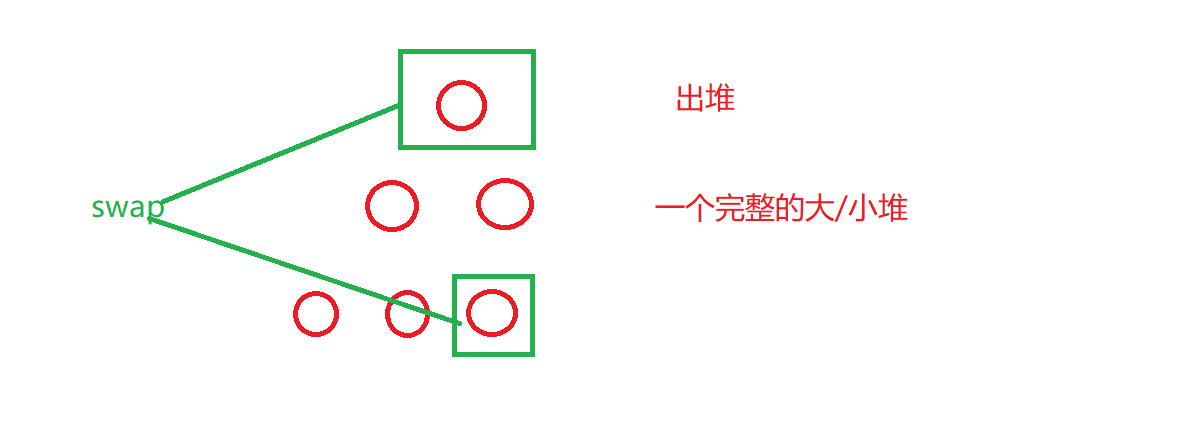
void pop(void)
{
std::swap(_con[0], _con[size() - 1]);
_con.pop_back();
AdjustDown(0);//Downward adjustment
}
void push(const T& val)
{
//Upward adjustment algorithm
_con.push_back(val);
AdjustUp(size()-1);
}
size_t size(void)
{
return _con.size();
}
bool empty(void)
{
return _con.empty();
}
T top(void)
{
return _con[0];
}
void AdjustUp(int child)
{
int parent = (child - 1) >> 1;
while (child > 0)
{
if (comp(_con[parent] , _con[child]))
{
::swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) >> 1;
}
else
break;
}
}
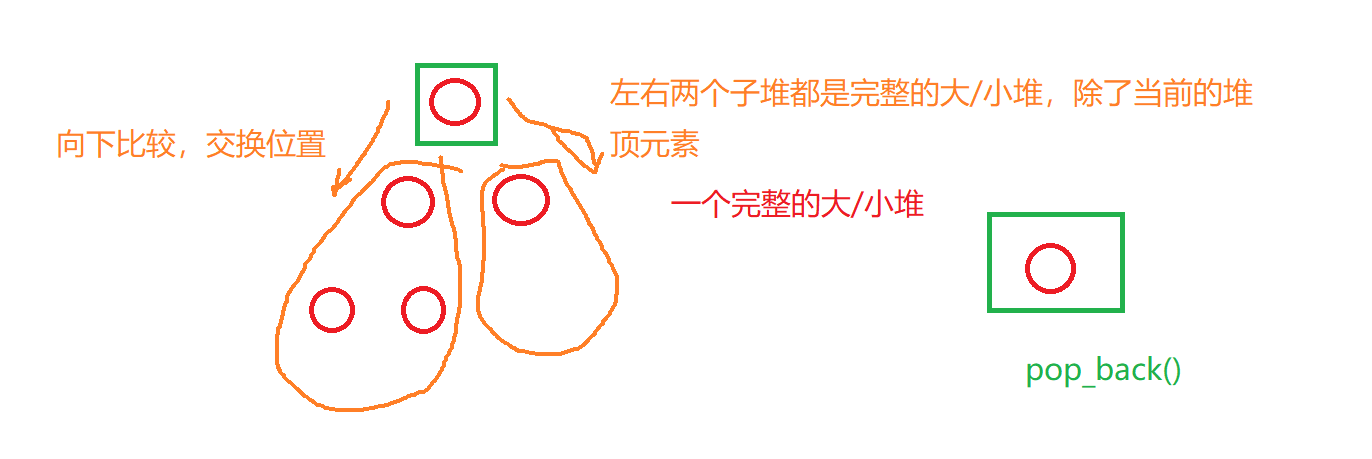
void AdjustDown(int parent)
{
int child = parent * 2 + 1;
int len = size();
while (child < len)
{
if (child + 1 < len && comp(_con[child], _con[child+1]))
{
child += 1;
}
if (comp(_con[parent], _con[child]))
{
::swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
private:
Container _con;
Compare comp;
};
}
Up adjustment algorithm and down adjustment algorithm
To sum up, when we put an element into the heap, we want to put the element on the last element of the array. At this time, we all assume / think that it is already a large / small heap. There is a problem with the last element and destroys the heap structure. We need to adjust this element and adjust it upward.
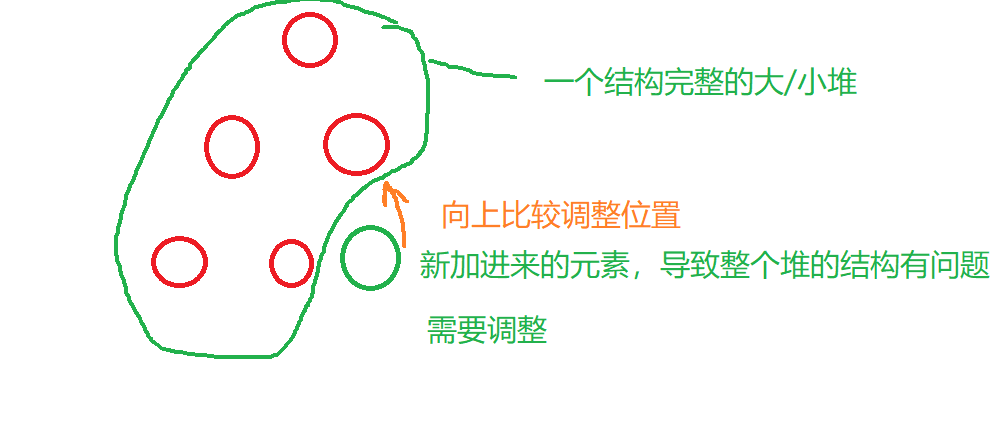
When we take an element out of the heap, we can only operate on the top of the heap element. Therefore, the top of the heap element is either the maximum value or the minimum value. Once pop, the integrity of the heap will be destroyed. Therefore, we generally choose to replace the last element to the top of the heap. In this way, except for the top of the heap element, the left and right sub heaps are all structurally complete Heap. Therefore, only the top element of the heap affects the integrity of the whole heap, so we need to compare and exchange this element downward. We need to use the downward adjustment algorithm.