Mahjong Foundation
Before introducing the code, let's introduce the basis of Mahjong:
There are 4 pieces of 10000-90000, 4 pieces of 1-9 cake, 4 pieces of 1-9 rope and 4 pieces of southeast and northwest white hair in a pair of mahjong cards
The three consecutive cards of 10000, cake and flower color are called shunzi, for example: 12000, 23000, 5, 6 and 7
Three cards of the same suit are called lettering, for example: 4 cakes, 4 cakes, 4 cakes, 9 cords, 9 cords and 9 cords
Two cards of the same suit are called pairs, such as 55000, Dongfeng and Dongfeng
In the article, 10000-90000 is defined as 1-9m, 1-9 cake is 1-9p, 1-9 rope is 1-9s, and 1-7z in white hair in southeast, northwest and northwest respectively. For example, 1 cake, 2 cakes and 3 cakes are 1p2p3p
Here is the basic formula of xiahu card: m shunzi + n engraved Zi + 1 pair (where m+n=4)
Just look at this formula, it may be a little abstract. It is understood that there is a pair in the hand, and the sum of the number of shunzi and engraved Zi is equal to 4, which is the Hu card.
In most areas, there are such rules: there are 13 CARDS + a touch card in your hand. If this touch card and the remaining 13 cards comply with the above Hu card formula, you can push the card and shout: "Hu!"
Why use pair method?
After talking so much, now let's get to the point: with c# how to determine whether a set of 14 cards meets the Hu card type? So let's talk about my method, the pair method, and the benefits of the pair method
To let the computer determine whether the hand is a Hu card, first let the computer know that there are several shunzi, engraved Zi and pairs in the hand, corresponding to the Hu card formula just introduced: m shunzi + n engraved Zi + 1 pair (where m+n=4). The first step is to decompose the hand, for example 4m5m6m 7p8p9p 6s6s, divide it into two shunzi and one engraved Zi, but if it is decomposed directly in the forward direction (that is, first decompose the shunzi Carver, and then decompose the pair). This will happen: 3m4m6m can be decomposed into a shunzi 3m4m5m, a carver 4m4m4m and an isolated card 6m, or two pairs 4m4m 4m4m and an isolated card 3m 5m6m. In this case, some card types may derive a variety of decomposition methods, which is not conducive to the rapid calculation of the program.
Although there are many cases of shunzi and Kezi, there is only one case of a pair. Therefore, first decompose the pair, then decompose the shunzi and the pair, and the situation will be reduced. Take the just 3m4m6m as an example, first decompose a pair of 4m4m, then decompose 3m4m5m, and the remaining 4m and 6m are isolated. In this way, we can immediately judge whether a set of hand meets the Hu card type. There are the most cards in a set There will only be 7 pairs, but shunzi and Kezi can combine a lot. If a deck of cards has no pairs, it can be immediately determined that no Hu cards can be played. Therefore, find out the pairs first, the decomposition is the least, and the program operation efficiency is the highest.
Procedural thinking
As mentioned above, 10000-90000 is defined as 1-9m, 1-9 cake as 1-9p, 1-9 rope as 1-9s, and 1-7z in the southeast, northwest and white hair respectively. This code is also used to replace the corresponding card in the c# program.
Let's start with an example of pairing method: 1m1m3m4m5m6m7m8m9m

This is the famous pure nine lotus treasure lamp
Use the pair method to find out the pair first, and then decompose the shunzi carving. There are only two pairs: 10000 and 90000
If 10000 pairs are found, the remaining cards will be broken down into 1m2m3m 4m5m6m 7m8m9m 9m9m, which is just in line with the Hu card formula
If you find out 90000 pairs, the remaining cards are 1m1m, 2m3m4m, 5m6m7m and 8m9m9m. At this time, the number of shunzi plus engravers is 3, which is not in line with the Hu card formula, but if you find out 10000 pairs, it is in line. This pair of cards is naturally the Hu card state.
Take another example: 3m3m7p8p9p3s4s4s5s5s6s7z7z7z

This set of cards has four pairs that can be found. It's obvious to find 30000, 7p8p9p and 7z7z7z first. The pile of cables needs a little analysis. You can also see the two shunzi of 3s4s5s and 4s5s6s. If you take four cables or five cables as pairs, 3S and 6s will be isolated. If you use Hongzhong as a pair, you can't form a Hu card. This shows that finding pairs first This method can greatly reduce the number and difficulty of judgment. If you want to calculate the number of times, you can also cover all cases.
source code
Code implementation principle: add the decomposed shunzi, engraved Zi and pairs to temp_brand_arr, and finally judge whether temp_brand_arr is null. If yes, it is impossible to Hu card. If not, it is that the hand is successfully decomposed into four faces + one pair, which can Hu card
The following is c# the source code of the implementation. If you don't understand anything, you can send me a private letter or add my QQ. The contact information is at the end of the article.
using System;
namespace mahjong
{
class Program
{
static void Main(string[] args)
{
while (true)
{
Console.Write("Please enter the card type:");
string input = Console.ReadLine();
Console.WriteLine(IfRon(input));
}
}
// Main function
private static string IfRon(string brand)
{
int count;
int brand_j;
int brand_k;
int brand_l;
string ifron = "No";
string[] brand_arr = new string[14]; //Array of cards passed in
string[] temp_brand_arr = new string[14]; //Array of cards output
for (int i = 0; i < 27; i += 2)
{
brand_arr[i / 2] = brand.Substring(i, 2); //Decompose string
}
for (int i = 0; i < 13; i++)
{
count = 0;
//Find the right one first
if (Array.IndexOf(temp_brand_arr, null) != -1)
{
for (int j = 0; j < brand_arr.Length; j++)
{
temp_brand_arr[j] = brand_arr[j];
}
}
if (temp_brand_arr[i] == temp_brand_arr[i + 1])
{
temp_brand_arr[i] = null;
temp_brand_arr[i + 1] = null;
for (int j = 0; j < 12; j++)
{
if (temp_brand_arr[j] == null)
{
continue;
}
for (int k = j + 1; k < 13;)
{
if (temp_brand_arr[k] == null)
{
k++;
continue;
}
if (temp_brand_arr[k][1] == temp_brand_arr[j][1])
{
brand_k = int.Parse("" + string.Format("{0}", temp_brand_arr[k][0]));
brand_j = int.Parse("" + string.Format("{0}", temp_brand_arr[j][0]));
if (brand_k == brand_j + 1 && temp_brand_arr[k][1] != 'z')
{
for (int l = k + 1; l < 14;)
{
if (temp_brand_arr[l] == null)
{
l++;
continue;
}
if (temp_brand_arr[l][1] == temp_brand_arr[k][1])
{
brand_l = int.Parse("" + string.Format("{0}", temp_brand_arr[l][0]));
if (brand_l == brand_k + 1)
{
temp_brand_arr[j] = null;
temp_brand_arr[k] = null;
temp_brand_arr[l] = null;
break;
}
else
{
l++;
}
}
else
{
break;
}
}
break;
}
else if (brand_k == brand_j)
{
for (int l = k + 1; l < 14;)
{
if (temp_brand_arr[l] == null)
{
l++;
continue;
}
if (temp_brand_arr[l][1] == temp_brand_arr[k][1])
{
brand_l = int.Parse("" + string.Format("{0}", temp_brand_arr[l][0]));
if (brand_l == brand_k)
{
temp_brand_arr[j] = null;
temp_brand_arr[k] = null;
temp_brand_arr[l] = null;
break;
}
else
{
l++;
}
}
else
{
break;
}
}
break;
}
else
{
k++;
}
}
else
{
break;
}
}
}
for (int j = 0; j < temp_brand_arr.Length; j++)
{
if (temp_brand_arr[j] == null)
{
count++;
}
}
if (count == 14)
{
ifron = "Yes";
return ifron;
}
}
}
return ifron;
}
}
}
Use example:
The last example can't be Hu because 3z4z5z it's westerly and northerly whiteboard, which can't form shunzi
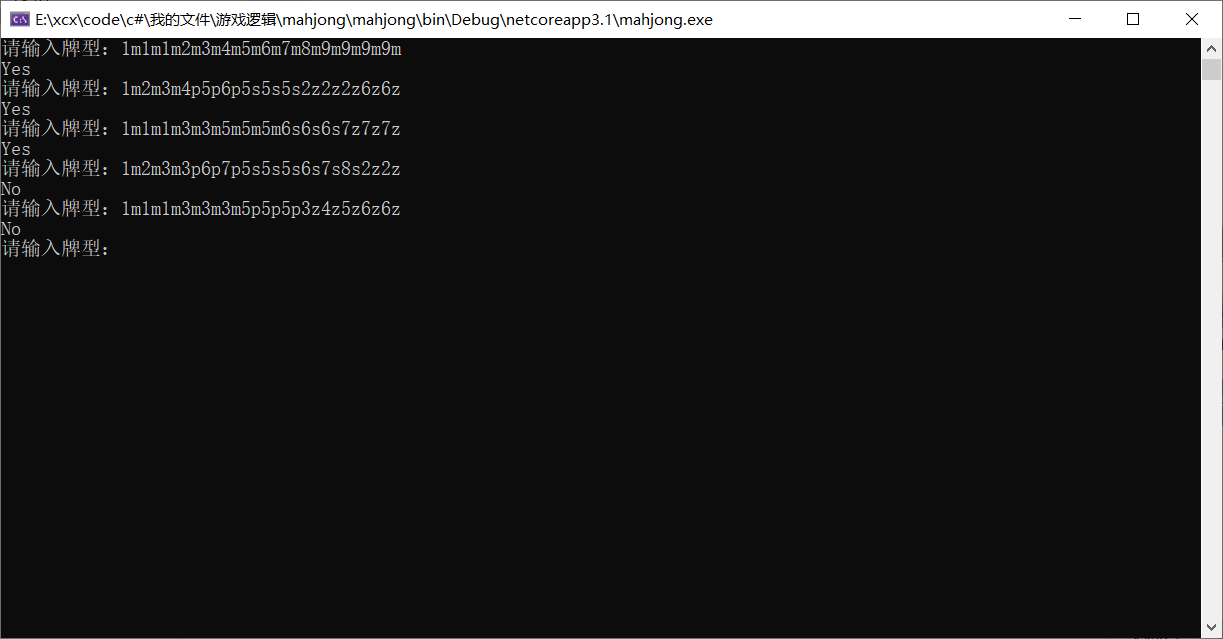
Here, the introduction of Hu card judgment algorithm is over. If you are interested in game development, please join our small group or add me to QQ research and discussion!
QQ:792006305
Group No.: 385075578