1. (1): judge whether open parentheses and closed parentheses in an arithmetic expression are paired.

Implementation code:

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct{
	char data[MAXSIZE];
	int top;
}seqstack;
int MatchCheck(char str[]){
	seqstack s;
	int i = 0;
	s.top = -1;
	while (str[i] != '\0'){
		// Open bracket encountered, stack
		if (str[i] == '(' || str[i] == '[' || str[i] == '{'){
			s.data[++s.top] = str[i];
		}
		// Close bracket encountered, out of stack 
		if (str[i] == ')'){
			if (s.data[s.top] == '(') s.top--;
			else return 0;
		}
		if (str[i] == ']'){ 
			if (s.data[s.top] == '[') s.top--;
			else return 0;
		}
		if (str[i] == '}'){
			if (s.data[s.top] == '{') s.top--;
			else return 0;
		}
		i++;
	}
	if (s.top >= 0) return 0;
	else return 1;
}
int main(){
	char str[20];
	int flag;
	printf("Please enter an arithmetic expression:\n");
	gets(str);
	flag = MatchCheck(str);
	if (flag == 1){
		printf("Open parentheses and closed parentheses are paired in this arithmetic expression!\n");
    }else{
		printf("The open parentheses and closed parentheses in this arithmetic expression are not paired!\n");
	}
	return 0;
}

Operation results:

The arithmetic expression entered is 9 * {8 + [7 - (6 + 5)]}:

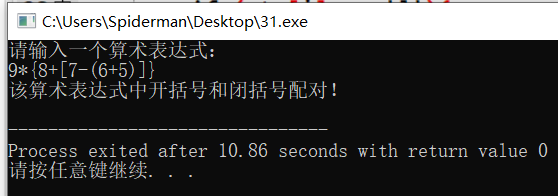
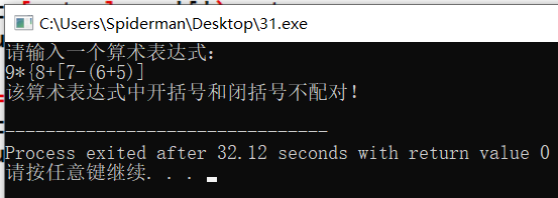
The arithmetic expression entered is 9 * {8 + [7 - (6 + 5)]:

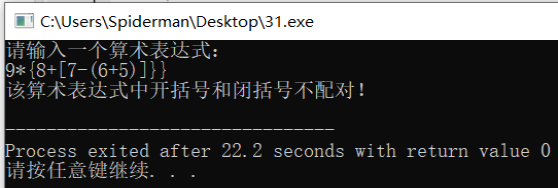
The arithmetic expression entered is 9 * {8 + [7 - (6 + 5)]}}:

analysis:

The time complexity and space complexity of the function used to check whether the open parentheses and closed parentheses in the arithmetic expression are paired are linear order O (n).

(2) : test the tower of Hanoi problem.

Let's first explain the Hanoi Tower problem:

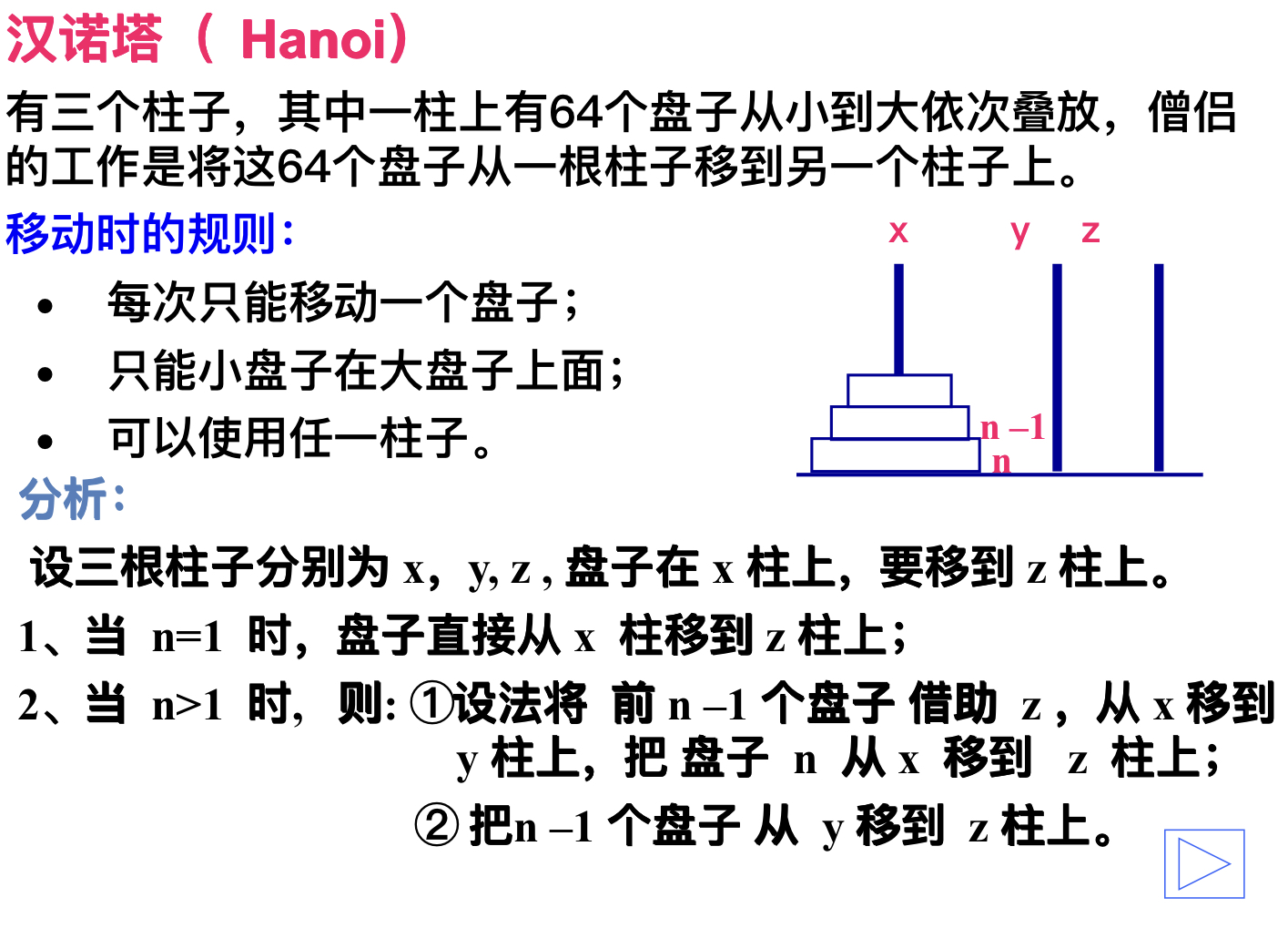
It should also be noted here that the recursive program execution needs to be realized with the help of the data structure of stack. The recursive call process is actually a process of entering and exiting the stack. Therefore, the recursive implementation of Hanoi tower here is actually implemented by stack.

Implementation code:

#include <stdio.h>
void move(char x,char y){
     printf("Remove a plate from%c Move column to%c Column.\n",x,y);
}
void Hanoi(int n,char x,char y,char z){
	if (n == 1)
	    move(x,z);
	else{
		Hanoi(n-1,x,z,y);
		move(x,z);
		Hanoi(n-1,y,x,z); 
	}
}
int main(){
	int n;
    printf("Please enter x Total number of plates on the column:");    
    scanf("%d",&n);
    printf("Start moving the plate.\n"); 
	Hanoi(n,'x','y','z');
	printf("The movement of the plate is complete."); 
	return 0;
}

Operation results:

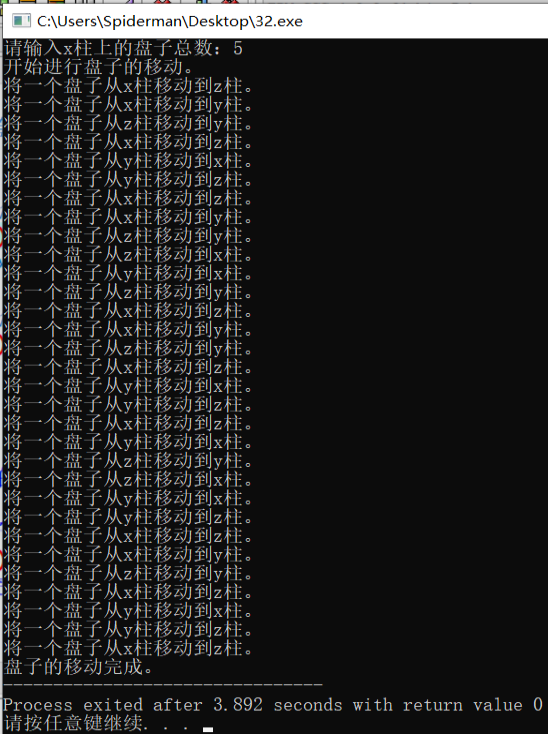
analysis:

The time complexity of the function used to recursively realize Hanoi Tower in this program is exponential order O (2^n), and the space complexity is linear order O (n).

(3) : suppose that the character sequence with the same forward reading and reverse reading is called "palindrome", try to write an algorithm to judge whether the read character sequence ending with '@' is "palindrome".

Here I want to explain that the way I judge palindromes here is to put the characters in the character sequence on the stack and in the queue one by one, and then use the properties of stack LIFO and queue FIFO to judge whether they are equal, so as to judge whether they are palindromes. There are many ways to judge palindromes. Here we use stacks and queues to judge. It is not recommended to judge according to my writing method. There are many better ways to judge, which are not specifically given here.

Implementation code:

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct{
	char data[MAXSIZE];
	int top;
}seqstack;
typedef struct{
	char data[MAXSIZE];
	int front;
	int rear;
}sequeue;
void SetSeqstackNULL(seqstack *s){
	s->top = -1;
}
void Push(seqstack *s,char x){
	if (s->top == MAXSIZE-1){
		printf("Stack overflow!\n");
	}else{
	    s->data[++s->top] = x;
	}
} 
char Pop(seqstack *s){
	if (s->top < 0){
		printf("Stack underflow!\n");
		return 0; 
	}else{
	    return (s->data[s->top--]);
	}
}
void SetSequeueNULL(sequeue *q){
	q->front = 0;
	q->rear = 0;
}
void EnQueue(sequeue *q,char x){
	if (q->front == (q->rear + 1) % MAXSIZE){
 	    printf("Queue full!\n");	
	}else{
	    q->data[++q->rear] = x;
	}
}
char DeQueue(sequeue *q){
	if (q->rear == q->front){
	    printf("The queue is empty!\n");
	    return 0;
	}else{
	    return q->data[++q->front];	 
	}
}
void HuiWenJudge(seqstack *s,sequeue *q){
	while (s->top >= 0){
		// Stack last in first out, queue first in first out, and use this property to judge palindromes 
		if (Pop(s) != DeQueue(q)){
			printf("This character sequence is not a palindrome!");
			return; 
		}
	}
	printf("The character sequence is "palindrome"!");
}
int main(){
	seqstack *s = (seqstack *)malloc(sizeof(seqstack));
	sequeue *q = (sequeue *)malloc(sizeof(sequeue));
	SetSeqstackNULL(s);
	SetSequeueNULL(q);
	char ch;
	printf("Please enter a character sequence in'@'Is terminator):\n");
	while ((ch = getchar()) != '@'){
		Push(s,ch);
		EnQueue(q,ch);
	}
	HuiWenJudge(s,q);
	return 0;
}

Operation results:


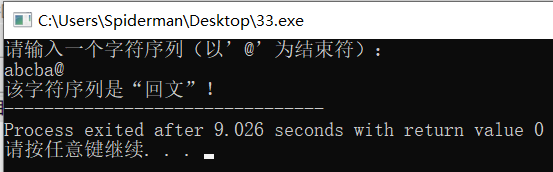
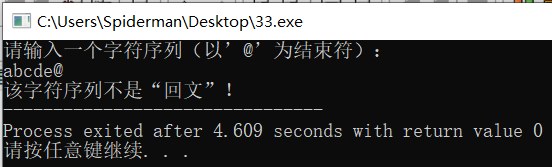
Operation results:
The time complexity of the function used for palindrome judgment in the program is linear order o (n). Assuming that n elements are stored in sequence stack s and sequence queue q, the space complexity of the function is O (n).

2. In the sequential storage structure, the input and output algorithms of two terminal cyclic queue with limited output are realized. Let each element represent a job to be processed, and the element value represents the expected time of the job. The simplified short job priority principle is adopted for entering the queue. If the estimated execution time of a newly submitted job is less than the average time of the job at the head and tail of the queue, it will be inserted at the head of the queue, otherwise it will be inserted at the tail of the queue.

Implementation code:

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100 
typedef struct{
	int data[MAXSIZE];
	int front;
	int rear;
}sequeue;
void SetNULL(sequeue *q){
	q->front = 0;
	q->rear = 0;
}
void EnQueue(sequeue *q,int x){
	int average;
	if((q->rear + 1) % MAXSIZE == q->front ){
		printf("Queue full!\n");
		return; 
	} 
	average = (q->data[q->rear] + q->data[(q->front + 1) % MAXSIZE]) / 2;
	if (x < average){
		q->data[q->front] = x;
		q->front = (q->front - 1) % MAXSIZE; 
	}else {
		q->rear = (q->rear + 1) % MAXSIZE; 
		q->data[q->rear] = x;
	}
}
void DeQueue(sequeue *q){
	if (q->front == q->rear){
		printf("The queue is empty!\n");
		return ; 
	}
	q->front = (q->front + 1) % MAXSIZE;
}
void PrintElem(sequeue *q){
	int i;
	for (i = q->front + 1;i <= q->rear;i++){
		printf("%d ",q->data[i]);
	}
}
int main(){
	sequeue *q = (sequeue *)malloc(sizeof(sequeue));
	int x,i;
	SetNULL(q);
    // Randomly create a queue to test the incoming and outgoing operations
	q->front = 2; 
	q->data[3] =  6;
	q->data[4] =  9;
	q->data[5] =  3;
	q->data[6] =  2;
	q->data[7] =  7;
	q->rear = 7;
	printf("All element values in the current queue are:");
	PrintElem(q); 
	printf("\n Conduct 5 consecutive team entry operations.");
    for (i = 0;i < 5;i++){
    	printf("\n The first%d Please enter the value of the element you want to join the queue:",i + 1); 
		scanf("%d",&x);
    	EnQueue(q,x);
    	printf("All element values in the current queue are:");
    	PrintElem(q);
	}
	printf("\n\n Conduct 5 consecutive out of team operations.");
    for (i = 0;i < 5;i++){
    	printf("\n The first%d Out of line operation.\n",i + 1); 
    	DeQueue(q);
    	printf("All element values in the current queue are:");
    	PrintElem(q);
	} 
	return 0;
}

Operation results:

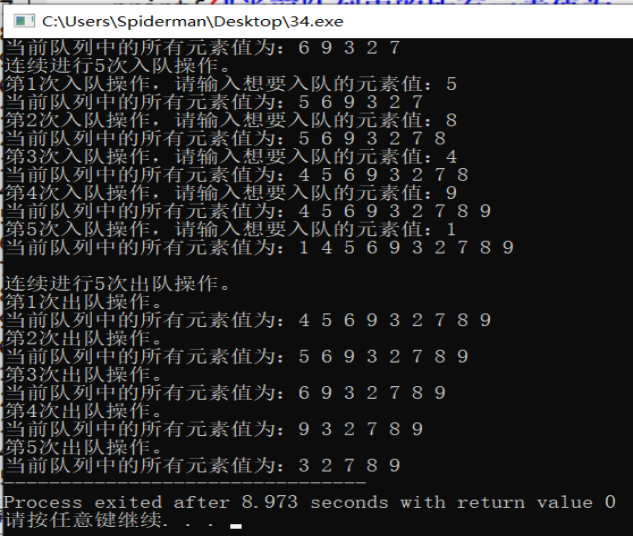
In this program, the time complexity of the in queue operation and out of queue operation of the two terminal cyclic queue with limited output is of constant order O (1), and the space complexity is of linear order O (n).