1. (1): write a program to establish a sequence table and output the values of all data elements in the sequence table one by one. Write the main function test results.

Implementation code:

#include<stdio.h>
#define MAXSIZE 100
typedef struct{
	int data[MAXSIZE];
	int last;
}sequenlist;
int main(){
	sequenlist s = {{5,2,4,9,6,7,1},6};
	printf("All elements in this sequence table are:");
	int i;
	for(i = 0;i <= s.last;i++){
	   printf("%d ",s.data[i]);
	}
	return 0;
}

Operation results:

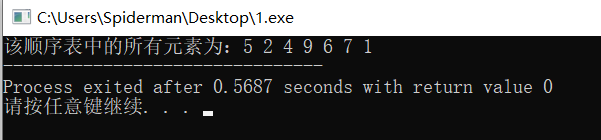
analysis:
The program establishes a sequence table, all elements of which are {5,2,4,9,6,7,1}, and outputs all elements in the sequence table one by one. When the last of the sequence table is n, the time complexity and space complexity of the program are linear order O (n).

(2) : write the sequence table positioning operation sub function to find out whether there is a data element X in the sequence table. If it exists, return the sequence number of the first data element with the same x value in the sequence table (the sequence number starts from 0); If it does not exist, return - 1. Write the main function test results.

Implementation code:

#include <stdio.h>
#define MAXSIZE 100
typedef struct{
    int data[MAXSIZE];
    int last;
}sequenlist;
int search(sequenlist *l,int x){
	int i,flag = -1;
	for(i = 0;i <= (*l).last;i++){
		if((*l).data[i]==x){
			flag = i;
			break;
		}
	}
	return flag; 
} 
int main(){
	sequenlist s = {{5,2,2,4,6,7,5},6};
	sequenlist *l = &s;
	printf("All elements in this sequence table are:");
	int i,x;
	for(i = 0;i <= s.last;i++){
	   printf("%d ",s.data[i]);
	}
	printf("\n Please enter the element you want to find:");
	scanf("%d",&x);
	printf("%d",search(l,x));
	return 0;
}

Operation results:


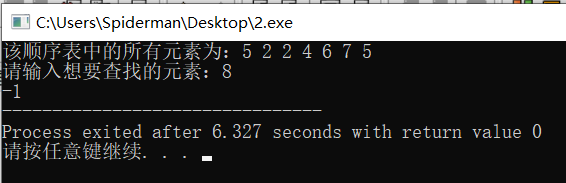
analysis:
The program writes a sequence table positioning operation sub function to find out whether there is a data element X in the sequence table. If the element to be searched exists, the sequence number of the first data element with the same x value in the sequence table is returned; If it does not exist, return - 1. As above, when 2 is entered, it exists and returns the serial number 1 of the first 2. When 8 is entered, it does not exist and returns - 1. The time complexity and space complexity of the positioning operation can be regarded as linear order O (n).

(3) : insert a new node x into the order table of increasing order to keep the order of the order table.
Solution idea: first find the insertion position, then shift, and finally insert; Starting from the first element, find the first element position I greater than the new node value x, which is the insertion position; Then, the elements will be moved back one position from the end of the table to element I; Finally, insert the new node x into position i.

Implementation code:

#include <stdio.h>
#define MAXSIZE 100
typedef struct{
    int data[MAXSIZE];
    int last;
}sequenlist;
void insert(sequenlist *l,int x){
	int i,j;
	for(i = 0;i <= (*l).last;i++){
	    if ((*l).data[i] > x){
		    break;
		}
	}
	for(j = (*l).last;j >= i;j--){
	    (*l).data[j+1] = (*l).data[j];
	}
	(*l).data[i] = x;
	(*l).last++;
}
int main(){
	sequenlist s = {{1,2,3,5,6,7},5};
	sequenlist *l = &s;
	printf("All elements in this sequence table are:");
	int i,j,x;
	for(i = 0;i <= s.last;i++){
	   printf("%d ",s.data[i]);
	}
	printf("\n Please enter the element you want to insert:");
	scanf("%d",&x);
	insert(l,x);
	printf("After inserting a new element, all elements in the sequence table are:");
	for(i = 0;i <= s.last;i++){
	   printf("%d ",s.data[i]);
	}
	return 0;
}

Operation results:


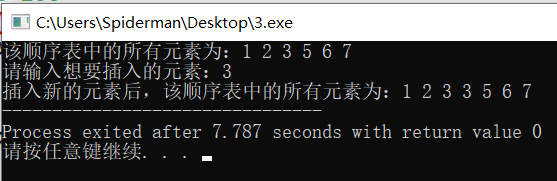
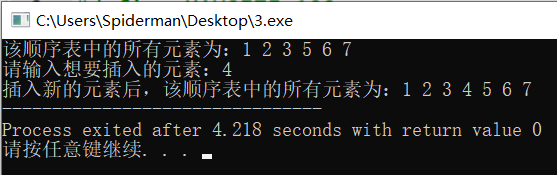
analysis:
The program inserts a new node x into the incremental order table according to the problem-solving idea, and maintains the order of the order table. As described above, when inserting element 3 that already exists in the sequence table, it is inserted normally and the order of the sequence table is maintained. When inserting element 4 that does not exist in the sequence table, it is inserted normally to the position that should be inserted, and the order of the sequence table is maintained after insertion. The time complexity and space complexity of the insertion operation can be regarded as linear order O (n).

(4) : delete all data elements equal to X in the sequence table.

Implementation code:

#include <stdio.h>
#define MAXSIZE 100
typedef struct{
    int data[MAXSIZE];
    int last;
}sequenlist;
int flag = 0; 
void delete(sequenlist *l,int x){
	int i,j;
	for (i = 0;i <= (*l).last;i++){
		if((*l).data[i] == x){
		   for (j = i + 1;j <= (*l).last;j++){
		   	    (*l).data[j-1] = (*l).data[j];
		   }
		   (*l).last--;
		   i--;
		   flag = 1;
		}
	}
}
int main(){
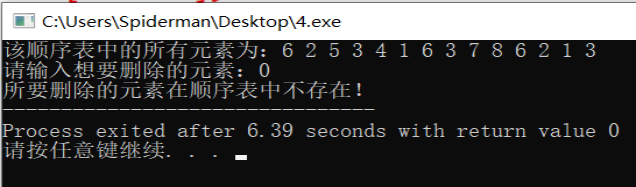
	sequenlist s = {{6,2,5,3,4,1,6,3,7,8,6,2,1,3},13};
	sequenlist *l = &s;
	printf("All elements in this sequence table are:");
	int i,j,x;
	for(i = 0;i <= s.last;i++){
	   printf("%d ",s.data[i]);
	}
	printf("\n Please enter the element you want to delete:");
	scanf("%d",&x);
	delete(l,x);
	if(flag){
	   printf("After deleting the corresponding element, all elements in the sequence table are:");
	   for(i = 0;i <= (*l).last;i++){
	       printf("%d ",(*l).data[i]);
	   }
	}else{
	   printf("The element to be deleted does not exist in the sequence table!");
	}
	return 0; 
}

Operation results:


analysis:
The program deletes all data elements equal to X in the sequence table. As above, when 6 is entered, all 6 elements in the sequence table are deleted. When 0 is entered, because 0 does not exist in the sequence table, it is output that it does not exist in the sequence table. The time complexity of the deletion operation can be regarded as the square order O (n) ²)， The spatial complexity can be regarded as linear order O (n).

2. It is known that the two sequential tables A and B are arranged in an increasing order according to the element value. It is required to write an algorithm to merge A and B into A sequential table arranged in an decreasing order according to the element value (the table is allowed to contain elements with the same value).

Implementation code:

#include <stdio.h>
#define MAXSIZE 100
typedef struct{
    int data[MAXSIZE];
    int last;
}sequenlist;
void MergeList(sequenlist *la,sequenlist *lb,sequenlist *lc){
	int i = (*la).last,j = (*lb).last,k = 0;
	while(i!=-1&&j!=-1){
	    if((*la).data[i] >= (*lb).data[j]){
	       (*lc).data[k++]=(*la).data[i];
	       i--;
		}else{
		   (*lc).data[k++]=(*lb).data[j];
		   j--;
		}
	}
	while(i!=-1){
	    (*lc).data[k++] = (*la).data[i];
	    i--;
	}
	while(j!=-1){
	 	(*lc).data[k++] = (*lb).data[j];
	 	j--;
	}
}
int main(){
	sequenlist a = {{1,2,3,5,7,8,9},6};
	sequenlist b = {{2,3,4,6,8,9,10},6};
	sequenlist c = {{0},a.last+b.last+1};
	sequenlist *la = &a;
	sequenlist *lb = &b;
	sequenlist *lc = &c;
    int i;
	printf("Sequence table a All elements in are:");
	for(i = 0;i <= a.last;i++){
	   printf("%d ",a.data[i]);
	}
	printf("\n Sequence table b All elements in are:");
	for(i = 0;i <= b.last;i++){
	   printf("%d ",b.data[i]);
	}
	MergeList(la,lb,lc);
	printf("\n Sequence table a And sequence table b After merging into a sequential table arranged in descending order according to element values, all elements in the resulting sequential table are:");
	for(i = 0;i <= c.last;i++){
	   printf("%d ",c.data[i]);
	}
	return 0;
}

Operation results:

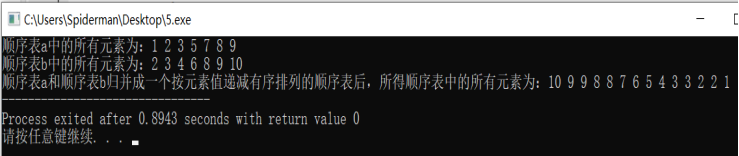
analysis:
The program combines two sequential tables a and b arranged in order of increasing element value into a sequential table arranged in order of decreasing element value, and the table is allowed to contain elements with the same value. As shown in the above results, the elements in the sequential table a arranged in order of increasing element value are {1,2,3,5,7,8,9}, and the elements in the sequential table b are {2,3,4,6,8,9,10} , the two sequential tables are merged into a sequential table arranged in descending order according to the element values, in which the elements are {10,9,9,8,8,7,6,5,4,3,3,2,2,1}. The time complexity of the merging operation can be regarded as linear order o (n), and the spatial complexity can be regarded as O (n+m).