Sorting algorithm

Bubble sort

Bubble Sort is a simple sorting algorithm.It repeatedly visits the columns to be sorted, comparing two elements at a time, and swapping them if their order (for example, from large to small, and from A to Z) is wrong.

Process demonstration:

#include <stdio.h>
void bubble_sort(int arr[], int len) {
    int i, j, temp;
    for (i = 0; i < len - 1; i++)
        for (j = 0; j < len - 1 - i; j++)
            if (arr[j] > arr[j + 1]) {
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
}
int main() {
    int arr[] = { 22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70 };
    // Get the total number of arr s, then each, and cast to int
    int len = (int) sizeof(arr) / sizeof(*arr);
    bubble_sort(arr, len);
    int i;
    for (i = 0; i < len; i++)
        printf("%d ", arr[i]);
    return 0;
}

Select Sort

Selection sort is a simple and intuitive sorting algorithm.It works as follows.First find the smallest (large) element in the unsorted sequence and store it at the beginning of the sorted sequence. Then continue to find the smallest (large) element from the remaining unsorted elements and place it at the end of the sorted sequence.And so on until all the elements are sorted.

Process demonstration:

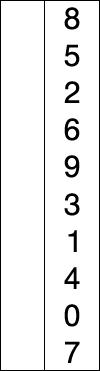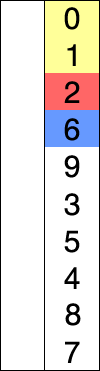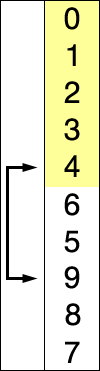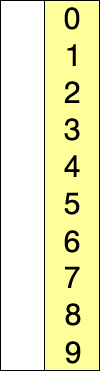
void swap(int *a,int *b) //Swap two variables
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
void selection_sort(int arr[], int len) 
{
    int i,j;
 
    for (i = 0 ; i < len - 1 ; i++) 
    {
        int min = i;
        for (j = i + 1; j < len; j++)     //Visit unsorted elements
            if (arr[j] < arr[min])    //Find the current minimum
                min = j;    //Record Minimum
           swap(&arr[min], &arr[i]);    //Exchange
    }
}

Insert Sort

Insertion Sort (English: Insertion Sort) is a simple and intuitive sorting algorithm.It works by building an ordered sequence, and for unsorted data, scanning backwards and forwards in the ordered sequence to find the corresponding location and insert it.Insert sorting is implemented by in-place sorting (that is, sorting using only the extra space of {\displaystyle O(1)} {\displaystyle O(1)}), so the sorted elements need to be moved backwards repeatedly during back-to-forward scanning to provide insert space for the latest elements.

Process demonstration:

void insertion_sort(int arr[], int len){
    int i,j,temp;
    for (i=1;i<len;i++){
            temp = arr[i];
            for (j=i;j>0 && arr[j-1]>temp;j--)
                    arr[j] = arr[j-1];
            arr[j] = temp;
    }
}

Shell Sort

Hill Sorting, also known as Decreasing Incremental Sorting, is a more efficient and improved version of Insert Sorting.Hill sorting is an unstable sorting algorithm.

Hill ordering is an improvement based on the following two properties of insertion ordering:

• Insert Sorting is efficient when operating on data that is almost sorted to achieve linear sorting efficiency
• But insert sorting is generally inefficient because insert sorting can only move data one bit at a time

Process demonstration:

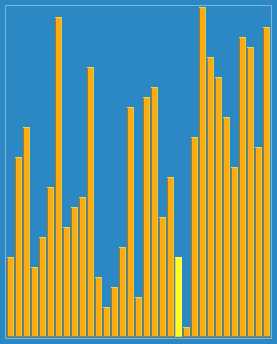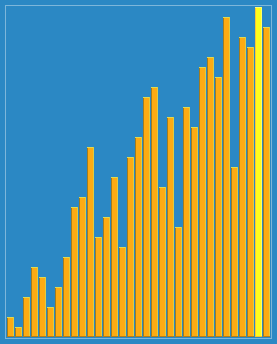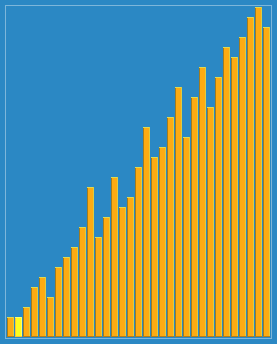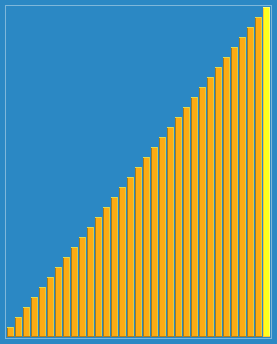
void shell_sort(int arr[], int len) {
    int gap, i, j;
    int temp;
    for (gap = len >> 1; gap > 0; gap = gap >> 1)
        for (i = gap; i < len; i++) {
            temp = arr[i];
            for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
                arr[j + gap] = arr[j];
            arr[j + gap] = temp;
        }
}

Merge Sort

Divide the data into two segments, moving the smallest elements from each to the end of the new data segment.

It can be done from top to bottom or from bottom to top.

Process demonstration:

iterative method

int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int* a = arr;
    int* b = (int*) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int* temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

Recursive method

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}
void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

Quick Sort

Randomly select one element in the interval as the baseline, place elements smaller than the baseline before the baseline, and elements larger than the baseline after the baseline, and then sort the decimal and majority areas respectively.

Process demonstration:

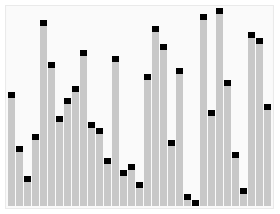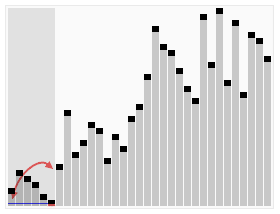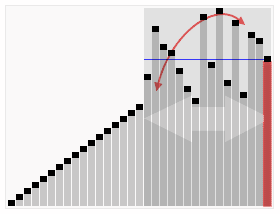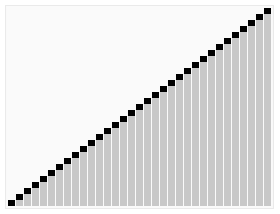
iterative method

typedef struct _Range {
    int start, end;
} Range;
Range new_Range(int s, int e) {
    Range r;
    r.start = s;
    r.end = e;
    return r;
}
void swap(int *x, int *y) {
    int t = *x;
    *x = *y;
    *y = t;
}
void quick_sort(int arr[], const int len) {
    if (len <= 0)
        return; // Avoid Segment Fault when len equals a negative value
    // R[]Simulated list, P is number, r[p++] is push,r[--p] is pop and takes element
    Range r[len];
    int p = 0;
    r[p++] = new_Range(0, len - 1);
    while (p) {
        Range range = r[--p];
        if (range.start >= range.end)
            continue;
        int mid = arr[(range.start + range.end) / 2]; // Select the middle point as the base point
        int left = range.start, right = range.end;
        do
        {
            while (arr[left] < mid) ++left;   // Detect if the left side of the datum meets the requirements
            while (arr[right] > mid) --right; //Detect whether the right side of the datum meets the requirements
 
            if (left <= right)
            {
                swap(&arr[left],&arr[right]);
                left++;right--;               // Move pointer to continue
            }
        } while (left <= right);
 
        if (range.start < right) r[p++] = new_Range(range.start, right);
        if (range.end > left) r[p++] = new_Range(left, range.end);
    }
}

Recursive method

void swap(int *x, int *y) {
    int t = *x;
    *x = *y;
    *y = t;
}
void quick_sort_recursive(int arr[], int start, int end) {
    if (start >= end)
        return;
    int mid = arr[end];
    int left = start, right = end - 1;
    while (left < right) {
        while (arr[left] < mid && left < right)
            left++;
        while (arr[right] >= mid && left < right)
            right--;
        swap(&arr[left], &arr[right]);
    }
    if (arr[left] >= arr[end])
        swap(&arr[left], &arr[end]);
    else
        left++;
    if (left)
        quick_sort_recursive(arr, start, left - 1);
    quick_sort_recursive(arr, left + 1, end);
}
void quick_sort(int arr[], int len) {
    quick_sort_recursive(arr, 0, len - 1);
}

Reference from: https://www.runoob.com/cprogramming/c-tutorial.html