Merge sorting is also called merge sorting. Its algorithm idea is to divide the sequence to be sorted into two parts, and then merge the two parts again. Only from the algorithmic idea to understand the merging and sorting will feel very abstract, and then to sequence A[0], A[l] , A[n-1] is explained in ascending order, and the top-down implementation method is adopted here.

Operation steps

(1) The sorting sequence to be sorted is divided into two parts. If the starting element subscript of the sequence to be sorted is first and the last element subscript is last, then the critical point subscript mid=(first+last)/2 between the two parts is A[first Mid] and A[mid+1 Last].

(2) Continue to divide the above two parts of the sequence according to step (1) until the length of the divided interval is 1.

(3) The sequence after the partition is merged and sorted. The sorting method is to merge the N subsequences into two subsequences to get n/2 or n/2+l subsequences with two elements, and then merge the subsequences to get an ordered sequence with length of n.

Sample merge sort

#include <stdio.h>
#include <stdlib.h>
#define N 7

void merge(int arr[], int low, int mid, int high){
    int i, k;
    int *tmp = (int *)malloc((high-low+1)*sizeof(int));
    //Request a space of two sizes
    int left_low = low;
    int left_high = mid;
    int right_low = mid + 1;
    int right_high = high;

    for(k=0; left_low<=left_high && right_low<=right_high; k++){  // Compare the elements that two pointers point to
        if(arr[left_low]<=arr[right_low]){
            tmp[k] = arr[left_low++];
        }else{
            tmp[k] = arr[right_low++];
        }
    }

    if(left_low <= left_high){  //If the first sequence has surplus, copy it directly and stick it to the end of the merged sequence
    //memcpy(tmp+k, arr+left_low, (left_high-left_low+l)*sizeof(int));
    for(i=left_low;i<=left_high;i++)
        tmp[k++] = arr[i];
    }

    if(right_low <= right_high){
    //If the second sequence has surplus, copy it directly and stick it to the end of the merged sequence
    //memcpy(tmp+k, arr+right_low, (right_high-right_low+1)*sizeof(int));
        for(i=right_low; i<=right_high; i++)
            tmp[k++] = arr[i];
    }

    for(i=0; i<high-low+1; i++)
        arr[low+i] = tmp[i];
    free(tmp);
    return;
}

void merge_sort(int arr[], unsigned int first, unsigned int last){
    int mid = 0;
    if(first<last){
        mid = (first+last)/2; /* Pay attention to prevent overflow */
        /*mid = first/2 + last/2;*/
        //mid = (first & last) + ((first ^ last) >> 1);
        merge_sort(arr, first, mid);
        merge_sort(arr, mid+1,last);
        merge(arr,first,mid,last);
    }
    return;
}

int main(){
    int i;
    int a[N]={32,12,56,78,76,45,36};

    printf ("Before sorting \n");
    for(i=0;i<N;i++)
        printf("%d\t",a[i]);

    merge_sort(a,0,N-1);  // sort

    printf ("\n After sorting \n");
    for(i=0;i<N;i++)
        printf("%d\t",a[i]); printf("\n");

    system("pause");
    return 0;
}

Operation result:
Before sorting

32    12    56    78    76    45    36

After sorting

12    32    36    45    56    76    78

The above program successfully implements the sorting operation for a given sequence by merging and sorting.

Flow chart of merging and sorting

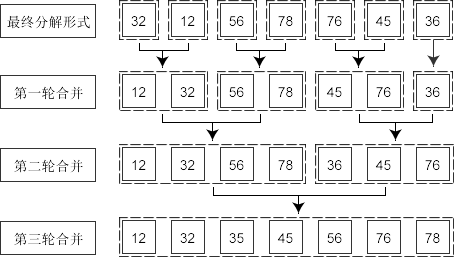
As shown in the above figure, the sequence to be sorted is first decomposed until it is divided into a single element, and then the two elements are combined. Because of the final decomposition into a single element, so when merging, put the decimal number in front, the large number behind, and get an ordered sequence. Next, sort the two consecutive ordered sequences. First, compare the first element of the ordered sequence, put the smaller element into the temporary array, and then compare the next element of the array where the smaller element is with the smaller element of the other array. Similarly, put the smaller element into the temporary array, and do it successively until all the elements of the two arrays are put into the temporary number Group, and finally put the elements of the temporary array into the corresponding positions in the original array.

Sweeping is more wonderful!!!