There is a problem worth discussing today. The problems are as follows:

  Enter an integer array and implement a function to adjust the order of numbers in the array so that all odd numbers in the array are in the first half of the array and all even numbers are in the second half of the array.

  First of all, we can write the contents of the main function smoothly, and then focus on the function used to adjust the array. The program is as follows:

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>

void print(int arr[], int sz)
{
    int i = 0;
    for(i = 0; i < sz; i++)
    {
        printf("%d", arr[i]);
    }
    printf("\n");
}

void move(int arr[], int sz)
{

}

int main()
{
    int arr[] = { 1,2,3,4,5,6,7,8,9,0 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    print(arr, sz);
    move(arr, sz);
    print(arr, sz);

    return 0;
}

  Here we choose to print the last function first, and then print out the array before executing the move function, so that we can compare it with the array adjusted by the move function later. Now let's focus on how to implement the move function.

  If we use common ideas, find the odd and even numbers in the array one by one, and then copy the array, as shown in the following figure:

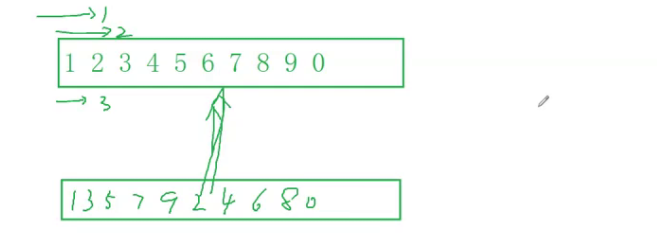
  In this way, at least three for loops will appear in the program. Although it is intuitive, there are better methods. Combined with the figure:

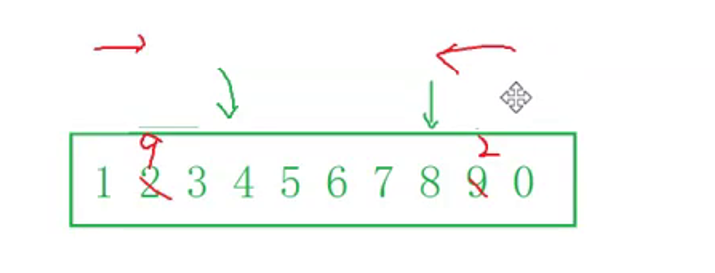
  We can find that every time we find an odd number, the odd number should be placed in the first half according to the title, so we can think like this. When the pointer looks from left to right, for example, 1 is an odd number, and then continue to look back. When we find 2, 2 is an even number. According to the meaning of the topic, we should put it behind. Now stop, look from right to left, and 0 is an even number, Look forward and find 9. 9 is an odd number. According to the meaning of the question, 9 should also be in the first half. Then stop at this time, and then exchange the position where it stopped at 2 just now with the position where it stopped at 9 this time, and so on. The left pointer looks back and the right pointer looks forward.

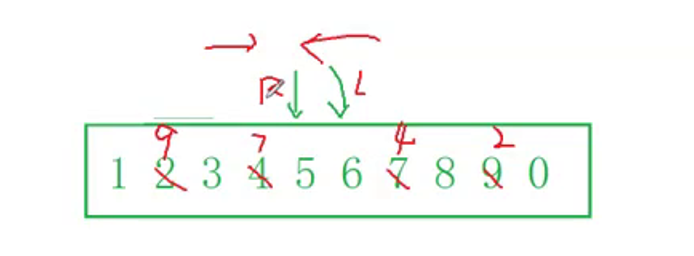
  Until we find the situation in the above figure, the left pointer L and the right pointer R, originally L is less than R, and there are elements in the middle that need us to move. But now, if it is like the situation in the above figure, it proves that all elements have been exchanged and the requirements of the problem have been completed, so this problem-solving method is more efficient.

  Now let's write the code. Use the pointer to write the left and right pointers, which are:

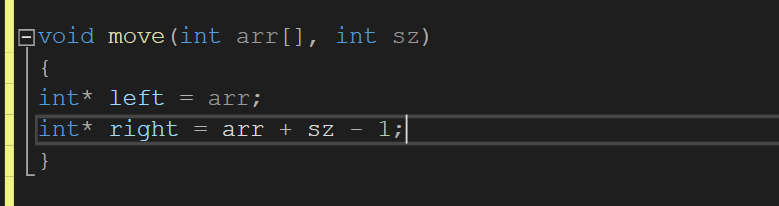
  Now write the following three steps into a program:

  (1) Find an even number from left to right

  (2) Find an odd number from right to left

  (3) Exchange of odd and even numbers

void move(int arr[], int sz)
{
    int* left = arr;
    int* right = arr + sz - 1;
//Find an even number from right to left and stop
    while(left < right)
    { 
        while((*left) % 2 == 1)
        {
            left++;
        }
//Find an odd number from right to left and stop
        while((*right) % 2 == 0)
        {
            right--;
        }   
//Odd and even exchange
        int tmp = *left;
        *left = *right;
        *right = tmp;

    }
}

    After writing here, you may think it is perfect, but it is not. There are still problems. We can run the program and have a look:

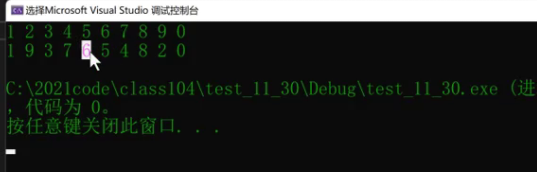
  It is not difficult to find that the positions of 6 and 5 are wrong. The problem is that the program just started exchanging odd and even numbers with tmp. Imagine if left and right go to the following figure:

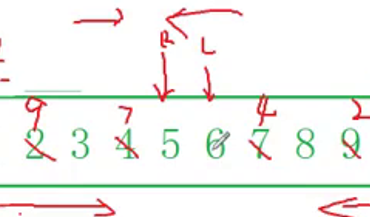
  If no judgment condition is added at this time, the left and right still perform the exchange, then the problems after the program execution will occur. Therefore, we need to add a judgment condition. When the left and right are staggered, do not exchange again. After improvement, the program should become the following figure:

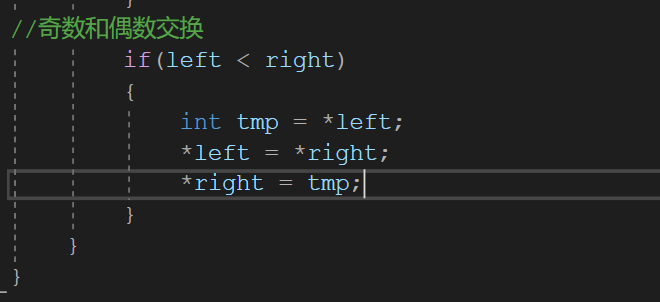
  At this point, the program runs again:

  You may not have any problem. You think it has been completed, but it is not. There are still problems with this writing method. Imagine that if all the numbers in this array are odd, the left pointer will find an even number from left to right, which will lead to cross-border access. If all the numbers are even, the right pointer will also lead to cross-border access, Therefore, there must be a parameter range when the pointer looks back. If the precondition is still left < right, the pointer will look for even numbers from front to back or odd numbers from back to front. After adding the corresponding conditions to this part, the code will be improved again to the following figure:

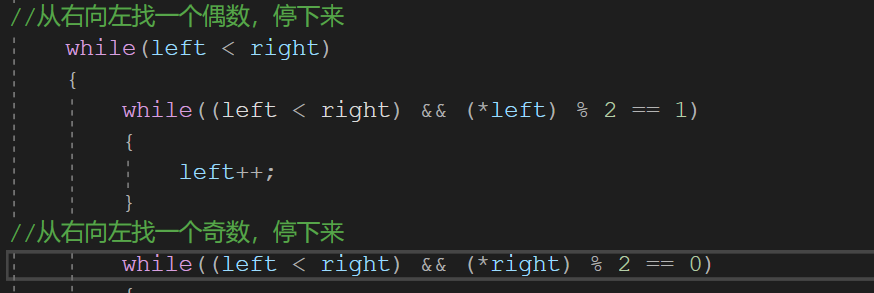
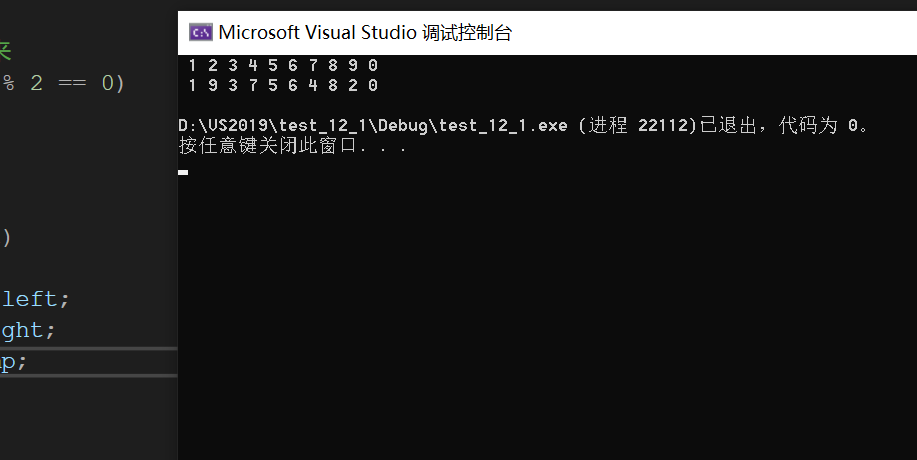
  Run the program again:

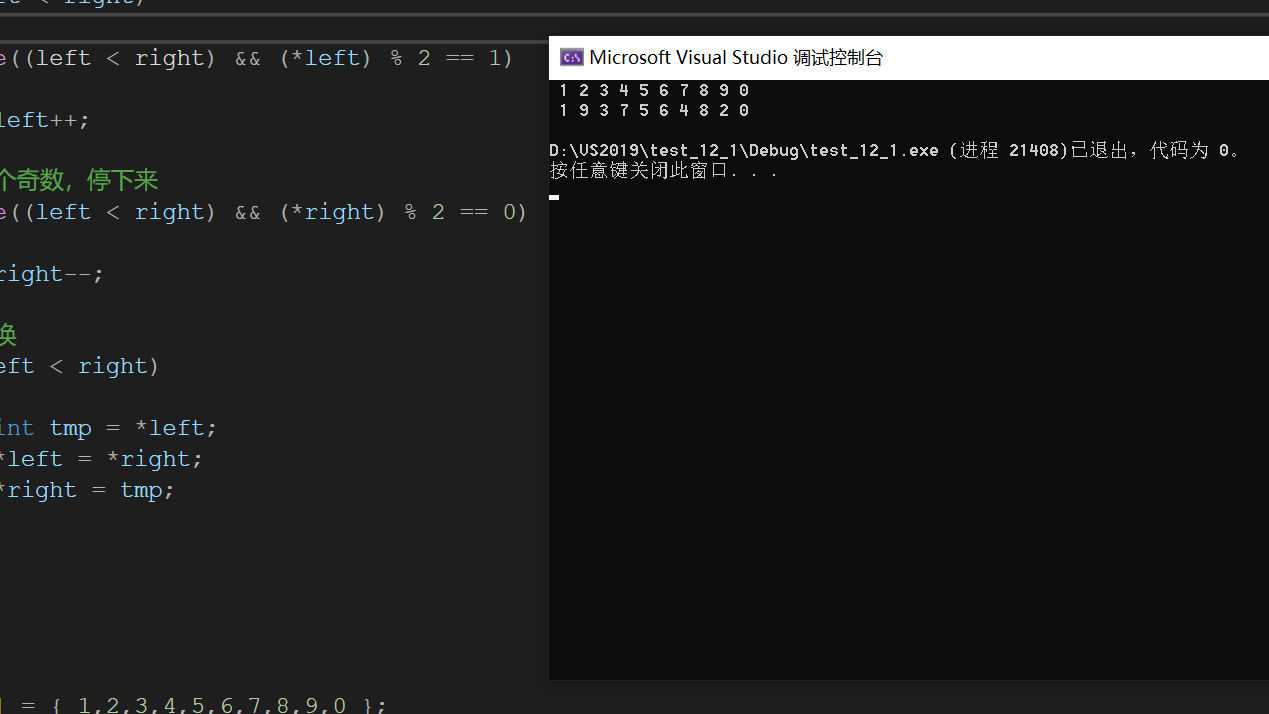
  This is the most perfect result in the end, so when writing code, you should consider all situations carefully. Otherwise, even in the past of vs compilation, other compilers may not be able to run in the past, because if you don't consider carefully, some examples will fail to pass the program, just like the cases just discussed are all odd or even numbers, so you should write the program more carefully!

  Finally, attach the complete code:

 

#define _CRT_SECURE_NO_WARNINGS 1

#include<stdio.h>

void print(int arr[], int sz)
{
    int i = 0;
    for(i = 0; i < sz; i++)
    {
        printf(" %d", arr[i]);
    }
    printf("\n");
}

void move(int arr[], int sz)
{
    int* left = arr;
    int* right = arr + sz - 1;
//Find an even number from right to left and stop
    while(left < right)
    { 
        while((left < right) && (*left) % 2 == 1)
        {
            left++;
        }
//Find an odd number from right to left and stop
        while((left < right) && (*right) % 2 == 0)
        {
            right--;
        }   
//Odd and even exchange
        if(left < right)
        {
            int tmp = *left;
            *left = *right;
            *right = tmp;
        }
    }
}

int main()
{
    int arr[] = { 1,2,3,4,5,6,7,8,9,0 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    print(arr, sz);
    move(arr, sz);
    print(arr, sz);

    return 0;
}