1, Recursion

The programming technique of program calling itself is called recursion
Recursion can usually transform a large and complex problem layer by layer into a smaller problem similar to the original problem
The main idea of recursion is to make big things small

2, Two necessary conditions for recursion

• There is a constraint. When this constraint is met, recursion will not continue
• Getting closer to this constraint after each recursive call

If the above conditions are not met during recursion, it is easy to report an error: stack overflow
The stack space allocated by the system to the program is limited, but there is an dead loop or (dead recursion), which will lead to the continuous development of stack space, and finally lead to the depletion of stack space, resulting in stack overflow error.

3, Recursive exercise

1. Print each bit of an integer value in sequence

  //For example, print each bit of 1234, separated by a space
  
  void Print(int num)   //1234, sequential printing
  {
     if(num/10 == 0)           //If the constraints are met, no recursion is allowed
	      printf("%d",num);
	 else
	 {
	      Print(num / 10);    //Each recursive call is getting closer and closer to the constraints
	      printf(num % 10);  
	 } 
  }
  
  int main()
  {
      int num = 0;
	  scanf("%d",&num);  //1234
	  Print(num);
      return 0;
  }    

2. Find the string length

int my_strlen(char* arr)
{
     if(*arr == '\0')  //If the constraints are met, no recursion is allowed
         return 0;
     else
         return 1 + my_strlen(arr+1);  //Each recursive call is getting closer and closer to the constraints
}
int main()
{
    char arr[20] = { 0 };
    scanf("%s",arr);         //abcde
    int len = my_strlen(arr);   
    printf("%d\n", len);   //5
    return 0;
}

3. Find the factorial of n

int factorial(int n)
{
     if(n == 1)       //If the constraints are met, no recursion is allowed
         return 1;
     else
         return n * factorial(n - 1);   //Each recursive call is getting closer and closer to the constraints
}
int main()
{
    int n = 0;
    scanf("%d",&n);
    int result = factorial(n);
    return 0;
}

4. Reverse string order

void reserve(char* str)   
{
	int left = 0;
	int right = strlen(str)-1;   
	char temp = str[left];
	if ( strlen(str) > 1  )   //Restrictions
	{
		str[left] = str[right];   
		str[right] = '\0';
		reserve(str + 1);    //Getting closer to this condition
		str[right] = temp;
	}
}
int main()
{
	char arr[20] = { 0};
	scanf("%s", arr);
	reserve(arr);
	printf("%s",arr);
}

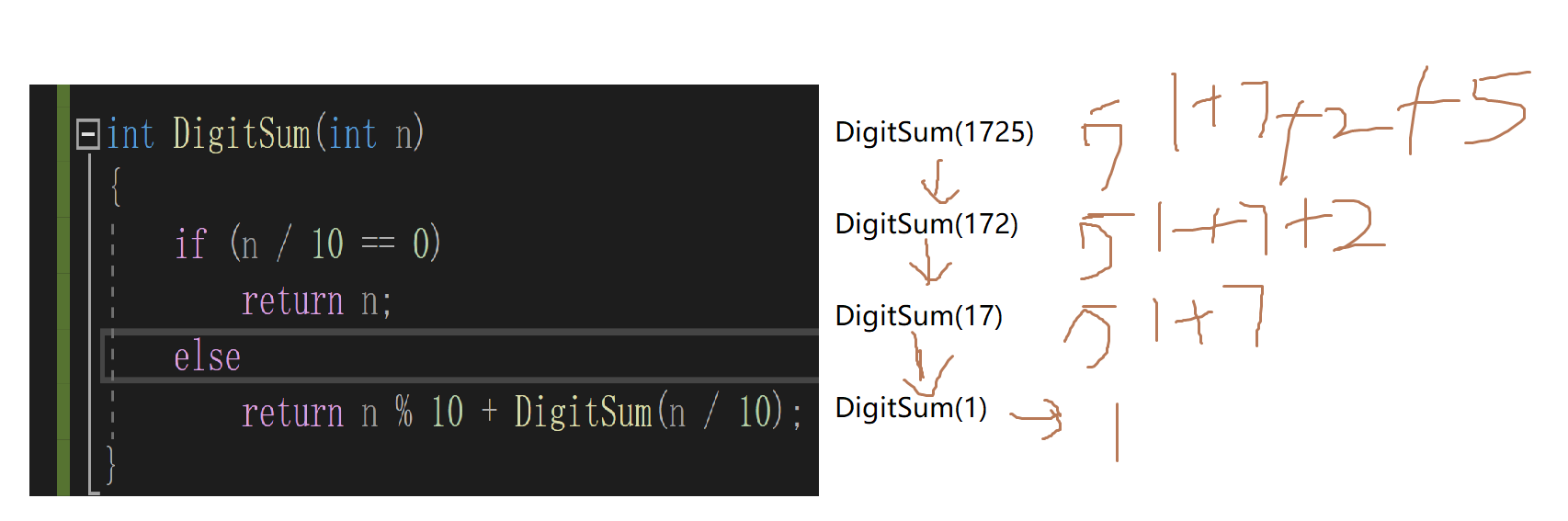
5. Find the sum of each number of integers

int DigitSum(int n)
{
	if (n / 10 == 0)      //Restrictions
		return n;
	else
		return n % 10 + DigitSum(n / 10);   //Getting closer to this condition
}
int main()
{
	int n = 0;
	scanf("%d",&n);
	int result = DigitSum(n);
	printf("%d", result);
}

6. Recursively find the nth Fibonacci number

Fibonacci sequence, also known as golden section sequence, was introduced by mathematician Leonardo Fibonacci taking rabbit breeding as an example, so it is also called "rabbit sequence", which refers to such a sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34
The logic of Fibonacci sequence is that the sum of the first two items is the third item
You can write its general mathematical formula:
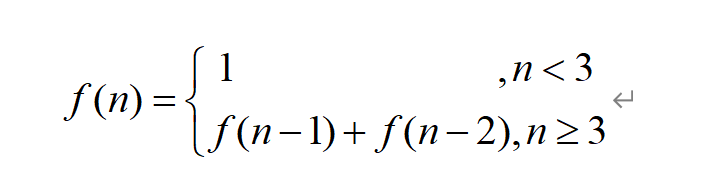Recursive Code:

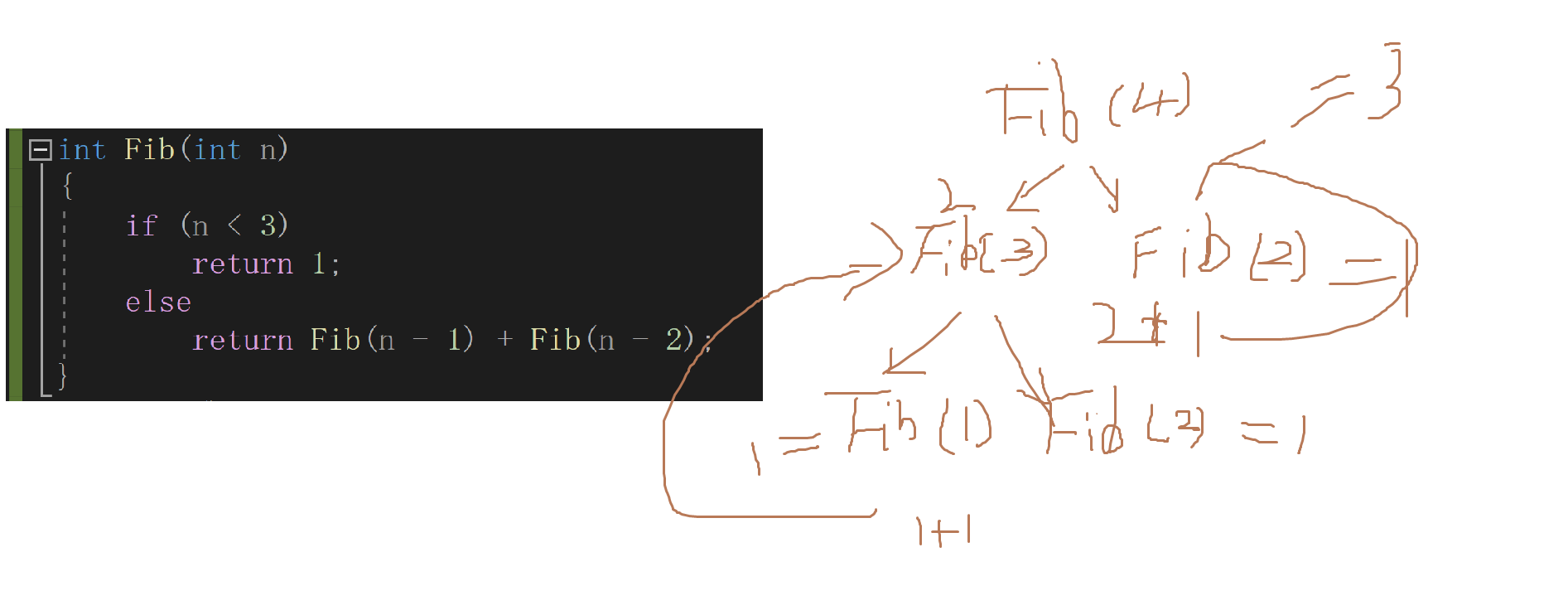
int Fib(int n)
{
	if (n < 3)            //Restrictions
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);  //Getting closer to this condition
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int result = Fib(n);
	printf("%d", result);
}

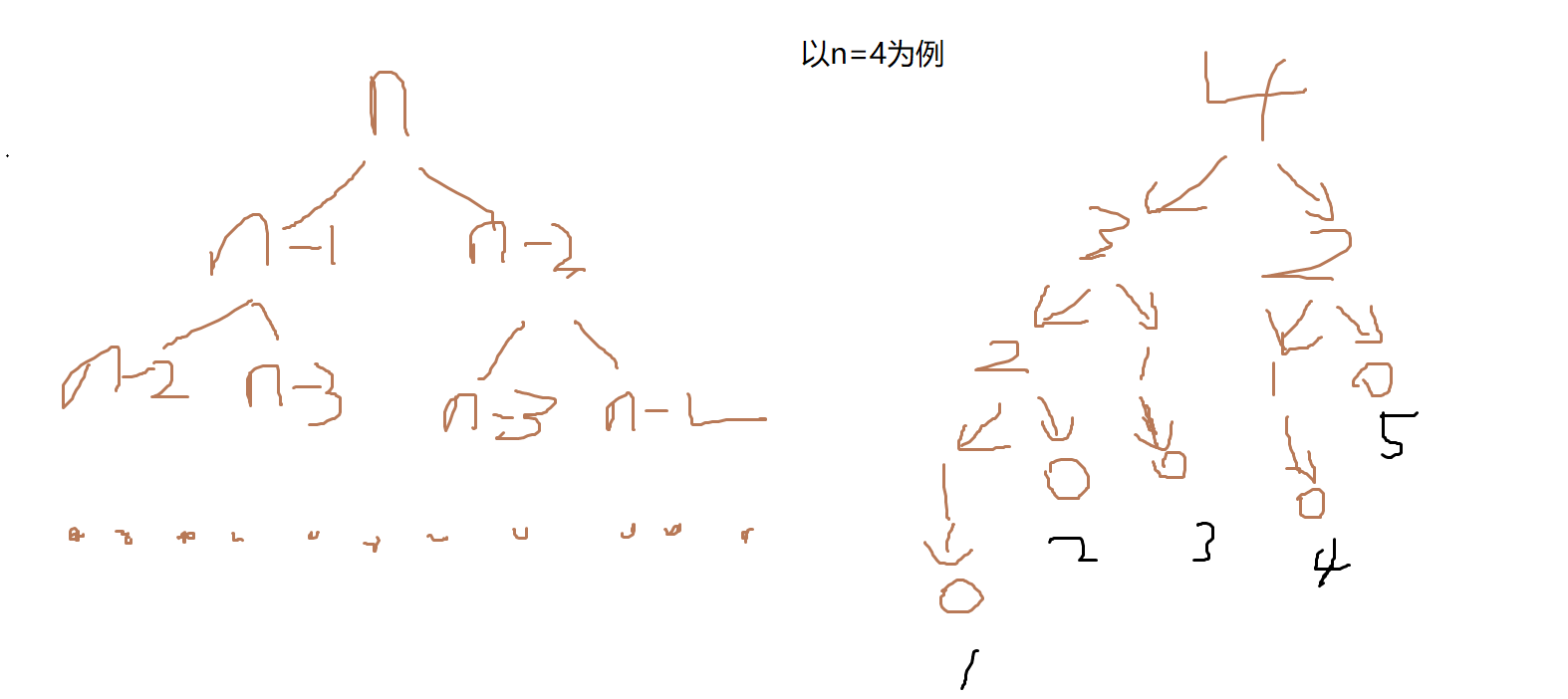
7. Solve the frog jumping problem recursively

Frog jumping problem: a frog can jump one step or two steps at a time. Ask how many jumping methods there are for frogs to jump n steps?

You can draw a flow chart to expand your ideas

You can write its general mathematical formula:

Recursive Code:

int forgJump(int n)
{

    if (n < 2)    //Restrictions
		return 1;
	else
		return forgJump(n - 1) + forgJump(n - 2);   //Getting closer to this condition
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int result = forgJump(n);
	printf("%d", result);
}

8. Tower of Hanoi

As shown in the figure below, there are three columns a, B and C from left to right. There are n discs stacked from small to large on column A. now it is required to move the disc on column a to column C. There is only one principle: only one plate can be moved at a time, and the large plate cannot be on the small plate. Calculate the moving steps and times

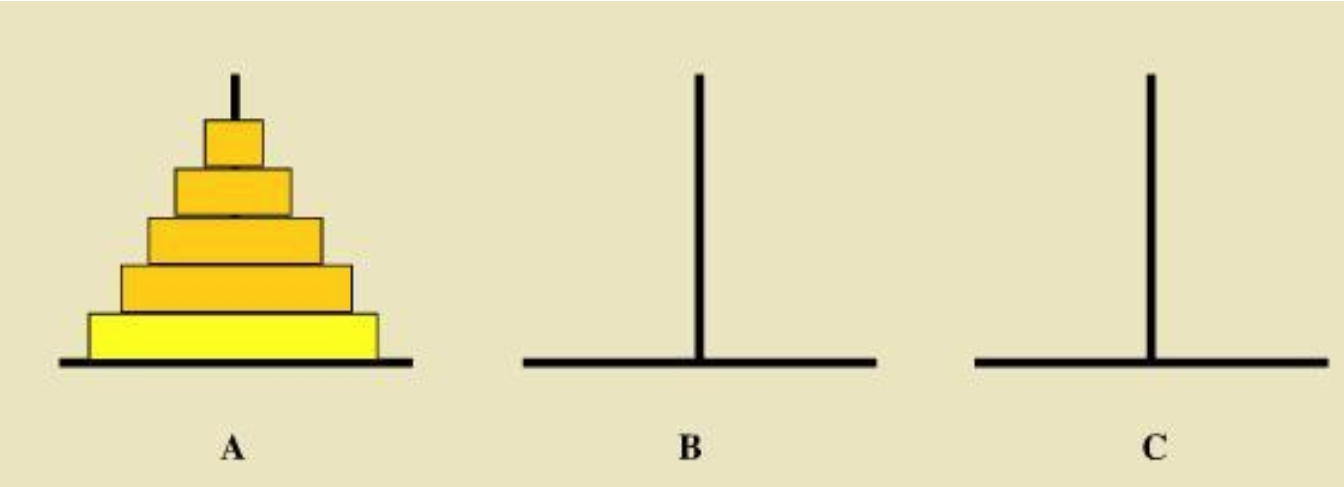
The implementation of this algorithm can be simply divided into three steps:

(1) Move n-1 plates from A to B;

(2) Move the n th plate from A to C;

(3) Move n-1 plates from B to C;

Starting from here, coupled with the analysis of the above mathematical problem solution, it is not difficult to find that the number of steps moved must be odd steps:

(1) The middle step is to move the largest plate from A to C;

(2) In the middle step, it can be seen that n-1 plates on A are moved to B by means of the auxiliary tower (tower C),

(3) In the middle step, it can be seen that n-1 plates on B are moved to C by means of auxiliary tower (tower A);

Steps and times of recursive implementation of Hanoi Tower:

void Hano_Tower(int n,char a ,char b ,char c)
{
	if (n == 1)             //Set constraints
		printf("%c--->%c\n", a, c);
	else
	{ 
		Hano_Tower(n - 1, a, c, b);   //Approach constraints
		printf("%c--->%c\n", a, c);
		Hano_Tower(n - 1, b, a, c);   //Approach constraints
	}
}
int main()
{
	int n = 0;
	char a = 'A';
	char b = 'B';
	char c = 'C';
	scanf("%d", &n);
	Hano_Tower(n,a,b,c);
	
}

The operation results are as follows:

Through the running results, it can be found that the number of plate moves is 2^n - 1, and the calculation is very simple.

#include<math.h>
int main()
{
    int n = 0;
    scanf("%d", &n);
    double num_move = pow(2, (double)n);
    printf("%.2lf", num_move);
}

The pow() function is a library function, double pow (double x, double y); Returns the value of X to the power of Y

When using, you need to include the header file math.h