Introduction to AES
AES (Advanced Encryption Standard), also known as Rijndael encryption method in cryptography, is a block encryption standard adopted by the federal government of the United States. This standard is used to replace the original DES, which has been widely used all over the world and has become one of the most popular symmetric key algorithms.
Before the advent of AES, the most commonly used symmetric key algorithm was DES Encryption Algorithms It's in In 1977, it was published as the commercial encryption standard of the U.S. government. The main problem of DES is that the key length is short, and it is not suitable for the requirement of data encryption security in distributed open network. Therefore, in 1998, the U.S. government decided not to continue using DES as the federal encryption standard, and launched a campaign to solicit AES candidate algorithms. The basic requirements for AES are: faster than triple DES, at least as secure as triple DES, 128 bits of data packet length and 128/192/256 bits of key length.
After more than three years of selection, the Rijndael algorithm designed by Belgian cryptographers finally emerged as a new generation of advanced encryption standards, which was published by the National Institute of Standards and Technology (NIST) in 2001. FIPS PUB 197.
Two, AES Algorithm principle
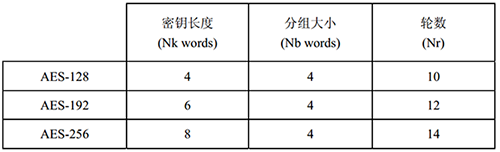
AES algorithm (Rijndael algorithm) is a symmetric block cipher algorithm. The length of the data packet must be 128 bits, and the length of the key used should be 128, 192 or 256 bits. For three AES algorithms with different key lengths, they are called "AES-128", "AES-192", "AES-256". (Rijndael The design can also handle other packet length and key length, but not in AES standard.
The following is the overall flow chart of AES encryption and decryption:
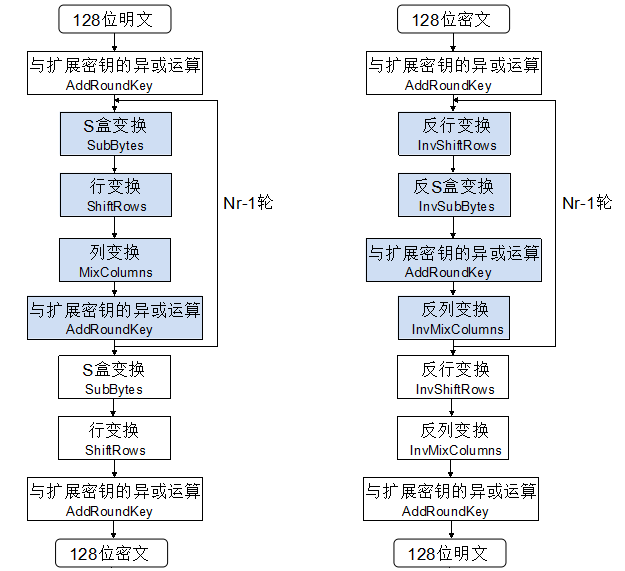
Here we need to know three symbols: Nb - the number of columns (32-bit words) contained in the State state State, that is, Nb=4; Nk—— The number of 32-bit words contained in the key, that is, Nk=4, 6 or 8; Nr - the number of rounds encrypted, for different key lengths, the number of rounds is different, as shown in the following figure:
The AES algorithm is divided into three parts: key expansion, block encryption and block decryption. I will try to be as concise as possible. If you don't understand it, please go to Google by yourself.
1) Key Extension
AES algorithm generates Nb(Nr+1) words by extending the key K input by the user through Key Expansion, and stores them in a linear array w[Nb*(Nr+1)]. Specifically as follows:
-
The position transformation function RotWord() accepts a word [a0, A1, a2, a3] as input, and output [a1, a2, a3, a0] after moving one byte to the left of the loop.
-
S-box transformation function SubWord(), accepts a word [a0, a1, a2, a3] as input. The S box is a 16x16 table, with each element being a byte. For each byte input, the first four bits constitute the hexadecimal number x as the line number, and the last four bits constitute the hexadecimal number y as the column number to find the corresponding values in the table. Finally, the function outputs a 32-bit word consisting of four new bytes.
-
Wheel constant Rcon [], how to calculate, let alone directly regard it as a constant array.
-
The first Nk elements of the extended key array w [] are external keys K, the subsequent element w[i] is equal to the previous element w[i-1] and the previous element w[i-1]. The exclusive or of the Nk elements w[i-Nk], i.e. w[i] = w[i-1] XOR w[i-Nk]; but if I is a multiple of Nk, w[i] = w[i-Nk] XOR SubWord(RotWord(w[i-1]) XOR Rcon[i/Nk-1].
Note that the fourth step above is suitable for AES-128 and AES-192. The detailed pseudocode is as follows:

C++ code for key extender (AES-128):
- #include <iostream>
- #include <bitset>
- using namespace std;
- typedef bitset<8> byte;
- typedef bitset<32> word;
- const int Nr = 10; //AES-128 requires 10 rounds of encryption
- const int Nk = 4; //Nk Represents the number of word s that are input keys
- byte S_Box[16][16] = {
- {0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76},
- {0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0},
- {0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15},
- {0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75},
- {0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84},
- {0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF},
- {0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8},
- {0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2},
- {0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73},
- {0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB},
- {0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79},
- {0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08},
- {0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A},
- {0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E},
- {0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF},
- {0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16}
- };
- //Round constant, used in key expansion. (AES-128 only takes 10 rounds)
- word Rcon[10] = {0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000,
- 0x20000000, 0x40000000, 0x80000000, 0x1b000000, 0x36000000};
- /**
- * Convert four byte s to one word.
- */
- word Word(byte& k1, byte& k2, byte& k3, byte& k4)
- {
- word result(0x00000000);
- word temp;
- temp = k1.to_ulong(); // K1
- temp <<= 24;
- result |= temp;
- temp = k2.to_ulong(); // K2
- temp <<= 16;
- result |= temp;
- temp = k3.to_ulong(); // K3
- temp <<= 8;
- result |= temp;
- temp = k4.to_ulong(); // K4
- result |= temp;
- return result;
- }
- /**
- * Cyclic left shift by byte
- * That is to say, [a0, a1, a2, a3] becomes [a1, a2, a3, a0]
- */
- word RotWord(word& rw)
- {
- word high = rw << 8;
- word low = rw >> 24;
- return high | low;
- }
- /**
- * S-box transformation for each byte in input word
- */
- word SubWord(word& sw)
- {
- word temp;
- for(int i=0; i<32; i+=8)
- {
- int row = sw[i+7]*8 + sw[i+6]*4 + sw[i+5]*2 + sw[i+4];
- int col = sw[i+3]*8 + sw[i+2]*4 + sw[i+1]*2 + sw[i];
- byte val = S_Box[row][col];
- for(int j=0; j<8; ++j)
- temp[i+j] = val[j];
- }
- return temp;
- }
- /**
- * Key Extension Function - Extended 128-bit key to w[4*(Nr+1)]
- */
- void KeyExpansion(byte key[4*Nk], word w[4*(Nr+1)])
- {
- word temp;
- int i = 0;
- //The first four of w [] are input key s
- while(i < Nk)
- {
- w[i] = Word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]);
- ++i;
- }
- i = Nk;
- while(i < 4*(Nr+1))
- {
- temp = w[i-1]; //Record the previous word
- if(i % Nk == 0)
- w[i] = w[i-Nk] ^ SubWord(RotWord(temp)) ^ Rcon[i/Nk-1];
- else
- w[i] = w[i-Nk] ^ temp;
- ++i;
- }
- }
- int main()
- {
- byte key[16] = {0x2b, 0x7e, 0x15, 0x16,
- 0x28, 0xae, 0xd2, 0xa6,
- 0xab, 0xf7, 0x15, 0x88,
- 0x09, 0xcf, 0x4f, 0x3c};
- word w[4*(Nr+1)];
- cout << "KEY IS: ";
- for(int i=0; i<16; ++i)
- cout << hex << key[i].to_ulong() << " ";
- cout << endl;
- KeyExpansion(key, w);
- //Testing
- for(int i=0; i<4*(Nr+1); ++i)
- cout << "w[" << dec << i << "] = " << hex << w[i].to_ulong() << endl;
- return 0;
- }
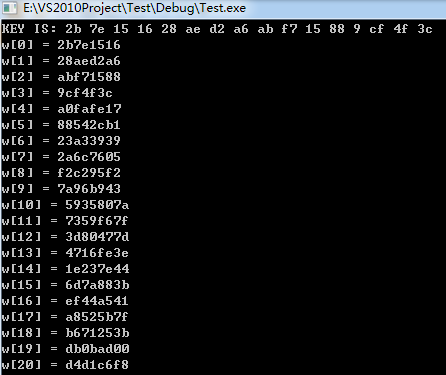
test Output results:
2) encryption
According to the overall flow chart of AES encryption (at the beginning of this article), the pseudocode is as follows:

From the pseudocode description, we can see that the subprograms involved in AES encryption are SubBytes(), ShiftRows(), MixColumns(), and AdRoundKey (). Let's introduce one by one:
① S-box transformation-SubBytes()
As already mentioned in the key extension section, the S-box is a table of 16 rows and 16 columns, in which each element is a byte. The S-box transformation is simple: the function SubBytes() accepts one The byte matrix of 4x4 is used as input. For each byte, the first four bits constitute the hexadecimal number x as the line number, and the last four bits constitute the hexadecimal number y as the column number. The corresponding values in the lookup table replace the bytes in the original position.
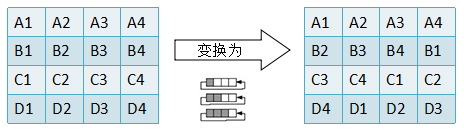
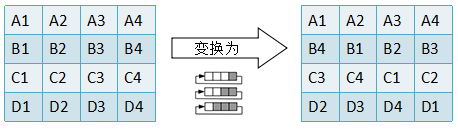
② Line transformation - ShiftRows()
Line transformation is also very simple. It simply shifts each row of the matrix in bytes: the first row remains unchanged, the second row moves one bit to the left, the third row moves two to the left, and the fourth row moves three to the left. As shown in the following figure:
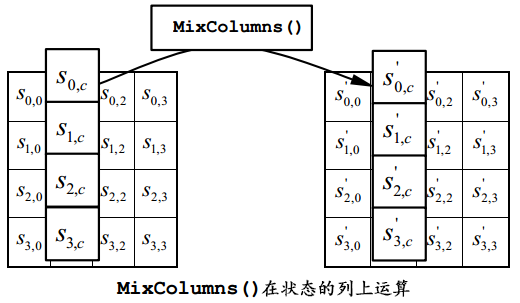
③ Column transformation - MixColumns()
The function MixColumns() also accepts a 4x4 byte matrix as input and transforms the matrix column by column in the following way:

Note that the multiplication used in the formula is Multiplication over Galois Fields (GF, Finite Fields) Advanced Encryption Standard Documents fips-197 As mentioned above, if you still don't understand, please Google yourself.
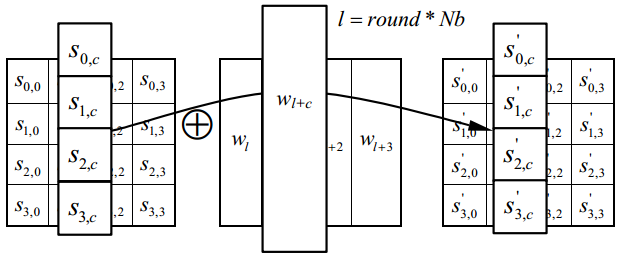
④ XOR-AddRoundKey() with Extended Key
Extended keys are only involved in this step. According to the number of rounds currently encrypted, four extended keys in w [] are bitwise exclusive or with four columns of the matrix. The following picture:
All right, here we are going to finish all the parts of AES encryption. The C++ source code implemented by the algorithm is in the third part after the article.
3) decryption
According to the overall flow chart of AES decryption (at the beginning of this article), the pseudocode is as follows:
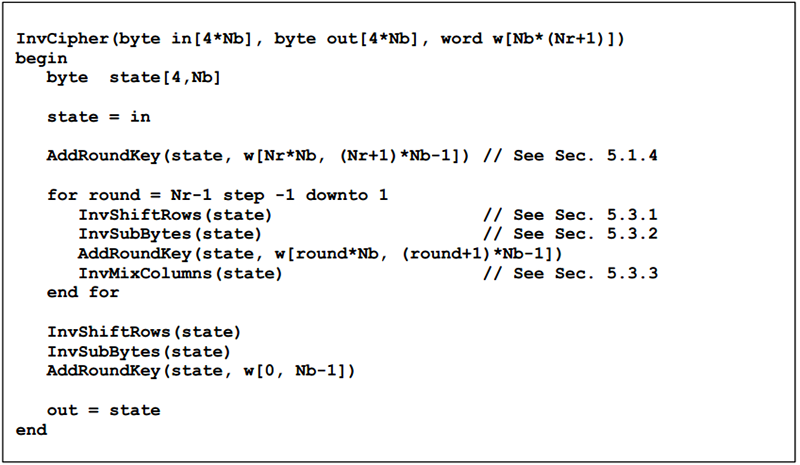
As can be seen from the pseudo code, we need to implement inversion transforms InvShiftRows(), InvSubBytes() and InvMixColumns() of S-box transformation, row transformation and column transformation, respectively. The following three inverse transformations are briefly discussed:
① Inverse transformation - InvShiftRows()
As mentioned above, ShiftRows() is a circular left shift for each row of a matrix, so InvShiftRows() is a circular right shift for each row of a matrix.
② Inverse S-box transformation-InvSubBytes()
Like S-box transformation, it looks up tables in the same way, except that it looks up another replacement table (S-Box inverse table).
③ Inverse transformation - InvMixColumns()
Just like column transformation, the coefficient matrix of the calculation formula has changed. The following picture:

Okay, AES decryption is over here. It is easy to implement AES decryption algorithm based on pseudo-code after writing three functions of inverse transformation.
C++ Implementation
Next, I use C++ to implement the encryption and decryption algorithm of AES, and realize the encryption and decryption of files. Here I use bitset of C++ STL to define two types: byte and word. It should be mentioned that for multiplication over finite fields, we can either look up tables (6 result tables) or write a function. Of course, looking up tables is more efficient, but considering posting code, here I use a function to achieve.
The following is the AES-128 source code for encrypting and decrypting a 128-bit data:
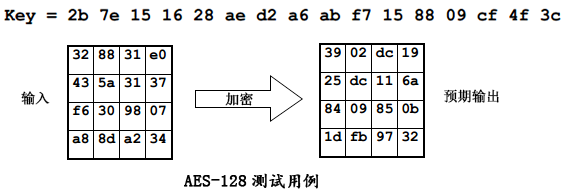
Examples of test purposes are as follows:
- /*************************************************************************
- > File Name: AES.cpp
- > Author: SongLee
- > E-mail: lisong.shine@qq.com
- > Created Time: 2014 Friday, December 12, 20:15, 50 seconds
- > Personal Blog: http://songlee24.github.com
- ************************************************************************/
- #include <iostream>
- #include <bitset>
- #include <string>
- using namespace std;
- typedef bitset<8> byte;
- typedef bitset<32> word;
- const int Nr = 10; //AES-128 requires 10 rounds of encryption
- const int Nk = 4; //Nk Represents the number of word s that are input keys
- byte S_Box[16][16] = {
- {0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76},
- {0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0},
- {0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15},
- {0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75},
- {0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84},
- {0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF},
- {0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8},
- {0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2},
- {0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73},
- {0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB},
- {0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79},
- {0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08},
- {0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A},
- {0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E},
- {0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF},
- {0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16}
- };
- byte Inv_S_Box[16][16] = {
- {0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB},
- {0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB},
- {0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E},
- {0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25},
- {0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92},
- {0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84},
- {0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06},
- {0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B},
- {0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73},
- {0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E},
- {0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B},
- {0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4},
- {0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F},
- {0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF},
- {0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61},
- {0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D}
- };
- //Round constant, used in key expansion. (AES-128 only takes 10 rounds)
- word Rcon[10] = {0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000,
- 0x20000000, 0x40000000, 0x80000000, 0x1b000000, 0x36000000};
- /**********************************************************************/
- /* */
- /* AES Algorithmic Implementation*/
- /* */
- /**********************************************************************/
- /******************************Here is the encrypted transformation function ****************************************************/
- /**
- * S Box Conversion - The first four bits are line numbers and the last four bits are column numbers
- */
- void SubBytes(byte mtx[4*4])
- {
- for(int i=0; i<16; ++i)
- {
- int row = mtx[i][7]*8 + mtx[i][6]*4 + mtx[i][5]*2 + mtx[i][4];
- int col = mtx[i][3]*8 + mtx[i][2]*4 + mtx[i][1]*2 + mtx[i][0];
- mtx[i] = S_Box[row][col];
- }
- }
- /**
- * Line Transform - Byte Cyclic Shift
- */
- void ShiftRows(byte mtx[4*4])
- {
- //The second line circle moves one bit to the left
- byte temp = mtx[4];
- for(int i=0; i<3; ++i)
- mtx[i+4] = mtx[i+5];
- mtx[7] = temp;
- //The third line circle moves two places to the left
- for(int i=0; i<2; ++i)
- {
- temp = mtx[i+8];
- mtx[i+8] = mtx[i+10];
- mtx[i+10] = temp;
- }
- //The fourth line moves three left circles
- temp = mtx[15];
- for(int i=3; i>0; --i)
- mtx[i+12] = mtx[i+11];
- mtx[12] = temp;
- }
- /**
- * Multiplication over Finite Fields GF(2^8)
- */
- byte GFMul(byte a, byte b) {
- byte p = 0;
- byte hi_bit_set;
- for (int counter = 0; counter < 8; counter++) {
- if ((b & byte(1)) != 0) {
- p ^= a;
- }
- hi_bit_set = (byte) (a & byte(0x80));
- a <<= 1;
- if (hi_bit_set != 0) {
- a ^= 0x1b; /* x^8 + x^4 + x^3 + x + 1 */
- }
- b >>= 1;
- }
- return p;
- }
- /**
- * Column transformation
- */
- void MixColumns(byte mtx[4*4])
- {
- byte arr[4];
- for(int i=0; i<4; ++i)
- {
- for(int j=0; j<4; ++j)
- arr[j] = mtx[i+j*4];
- mtx[i] = GFMul(0x02, arr[0]) ^ GFMul(0x03, arr[1]) ^ arr[2] ^ arr[3];
- mtx[i+4] = arr[0] ^ GFMul(0x02, arr[1]) ^ GFMul(0x03, arr[2]) ^ arr[3];
- mtx[i+8] = arr[0] ^ arr[1] ^ GFMul(0x02, arr[2]) ^ GFMul(0x03, arr[3]);
- mtx[i+12] = GFMul(0x03, arr[0]) ^ arr[1] ^ arr[2] ^ GFMul(0x02, arr[3]);
- }
- }
- /**
- * Round Key Plus Transform - XOR each column with the extended key
- */
- void AddRoundKey(byte mtx[4*4], word k[4])
- {
- for(int i=0; i<4; ++i)
- {
- word k1 = k[i] >> 24;
- word k2 = (k[i] << 8) >> 24;
- word k3 = (k[i] << 16) >> 24;
- word k4 = (k[i] << 24) >> 24;
- mtx[i] = mtx[i] ^ byte(k1.to_ulong());
- mtx[i+4] = mtx[i+4] ^ byte(k2.to_ulong());
- mtx[i+8] = mtx[i+8] ^ byte(k3.to_ulong());
- mtx[i+12] = mtx[i+12] ^ byte(k4.to_ulong());
- }
- }
- /**************************Here is the decrypted inverse transform function *******************************************************/
- /**
- * Inverse S-box transformation
- */
- void InvSubBytes(byte mtx[4*4])
- {
- for(int i=0; i<16; ++i)
- {
- int row = mtx[i][7]*8 + mtx[i][6]*4 + mtx[i][5]*2 + mtx[i][4];
- int col = mtx[i][3]*8 + mtx[i][2]*4 + mtx[i][1]*2 + mtx[i][0];
- mtx[i] = Inv_S_Box[row][col];
- }
- }
- /**
- * Reverse Transform - Cyclic Right Shift in Bytes
- */
- void InvShiftRows(byte mtx[4*4])
- {
- //The second line circle moves one bit to the right
- byte temp = mtx[7];
- for(int i=3; i>0; --i)
- mtx[i+4] = mtx[i+3];
- mtx[4] = temp;
- //The third line circle moves two to the right
- for(int i=0; i<2; ++i)
- {
- temp = mtx[i+8];
- mtx[i+8] = mtx[i+10];
- mtx[i+10] = temp;
- }
- //Fourth line circle moves three to the right
- temp = mtx[12];
- for(int i=0; i<3; ++i)
- mtx[i+12] = mtx[i+13];
- mtx[15] = temp;
- }
- void InvMixColumns(byte mtx[4*4])
- {
- byte arr[4];
- for(int i=0; i<4; ++i)
- {
- for(int j=0; j<4; ++j)
- arr[j] = mtx[i+j*4];
- mtx[i] = GFMul(0x0e, arr[0]) ^ GFMul(0x0b, arr[1]) ^ GFMul(0x0d, arr[2]) ^ GFMul(0x09, arr[3]);
- mtx[i+4] = GFMul(0x09, arr[0]) ^ GFMul(0x0e, arr[1]) ^ GFMul(0x0b, arr[2]) ^ GFMul(0x0d, arr[3]);
- mtx[i+8] = GFMul(0x0d, arr[0]) ^ GFMul(0x09, arr[1]) ^ GFMul(0x0e, arr[2]) ^ GFMul(0x0b, arr[3]);
- mtx[i+12] = GFMul(0x0b, arr[0]) ^ GFMul(0x0d, arr[1]) ^ GFMul(0x09, arr[2]) ^ GFMul(0x0e, arr[3]);
- }
- }
- /******************************Following is the key extension section ***************************************************************/
- /**
- * Convert four byte s to one word.
- */
- word Word(byte& k1, byte& k2, byte& k3, byte& k4)
- {
- word result(0x00000000);
- word temp;
- temp = k1.to_ulong(); // K1
- temp <<= 24;
- result |= temp;
- temp = k2.to_ulong(); // K2
- temp <<= 16;
- result |= temp;
- temp = k3.to_ulong(); // K3
- temp <<= 8;
- result |= temp;
- temp = k4.to_ulong(); // K4
- result |= temp;
- return result;
- }
- /**
- * Cyclic left shift by byte
- * That is to say, [a0, a1, a2, a3] becomes [a1, a2, a3, a0]
- */
- word RotWord(word& rw)
- {
- word high = rw << 8;
- word low = rw >> 24;
- return high | low;
- }
- /**
- * S-box transformation for each byte in input word
- */
- word SubWord(word& sw)
- {
- word temp;
- for(int i=0; i<32; i+=8)
- {
- int row = sw[i+7]*8 + sw[i+6]*4 + sw[i+5]*2 + sw[i+4];
- int col = sw[i+3]*8 + sw[i+2]*4 + sw[i+1]*2 + sw[i];
- byte val = S_Box[row][col];
- for(int j=0; j<8; ++j)
- temp[i+j] = val[j];
- }
- return temp;
- }
- /**
- * Key Extension Function - Extended 128-bit key to w[4*(Nr+1)]
- */
- void KeyExpansion(byte key[4*Nk], word w[4*(Nr+1)])
- {
- word temp;
- int i = 0;
- //The first four of w [] are input key s
- while(i < Nk)
- {
- w[i] = Word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]);
- ++i;
- }
- i = Nk;
- while(i < 4*(Nr+1))
- {
- temp = w[i-1]; //Record the previous word
- if(i % Nk == 0)
- w[i] = w[i-Nk] ^ SubWord(RotWord(temp)) ^ Rcon[i/Nk-1];
- else
- w[i] = w[i-Nk] ^ temp;
- ++i;
- }
- }
- /******************************Here are the encryption and decryption functions ********************************************************************/
- /**
- * encryption
- */
- void encrypt(byte in[4*4], word w[4*(Nr+1)])
- {
- word key[4];
- for(int i=0; i<4; ++i)
- key[i] = w[i];
- AddRoundKey(in, key);
- for(int round=1; round<Nr; ++round)
- {
- SubBytes(in);
- ShiftRows(in);
- MixColumns(in);
- for(int i=0; i<4; ++i)
- key[i] = w[4*round+i];
- AddRoundKey(in, key);
- }
- SubBytes(in);
- ShiftRows(in);
- for(int i=0; i<4; ++i)
- key[i] = w[4*Nr+i];
- AddRoundKey(in, key);
- }
- /**
- * Decrypt
- */
- void decrypt(byte in[4*4], word w[4*(Nr+1)])
- {
- word key[4];
- for(int i=0; i<4; ++i)
- key[i] = w[4*Nr+i];
- AddRoundKey(in, key);
- for(int round=Nr-1; round>0; --round)
- {
- InvShiftRows(in);
- InvSubBytes(in);
- for(int i=0; i<4; ++i)
- key[i] = w[4*round+i];
- AddRoundKey(in, key);
- InvMixColumns(in);
- }
- InvShiftRows(in);
- InvSubBytes(in);
- for(int i=0; i<4; ++i)
- key[i] = w[i];
- AddRoundKey(in, key);
- }
- /**********************************************************************/
- /* */
- /* Testing*/
- /* */
- /**********************************************************************/
- int main()
- {
- byte key[16] = {0x2b, 0x7e, 0x15, 0x16,
- 0x28, 0xae, 0xd2, 0xa6,
- 0xab, 0xf7, 0x15, 0x88,
- 0x09, 0xcf, 0x4f, 0x3c};
- byte plain[16] = {0x32, 0x88, 0x31, 0xe0,
- 0x43, 0x5a, 0x31, 0x37,
- 0xf6, 0x30, 0x98, 0x07,
- 0xa8, 0x8d, 0xa2, 0x34};
- //Output key
- cout << "The key is:";
- for(int i=0; i<16; ++i)
- cout << hex << key[i].to_ulong() << " ";
- cout << endl;
- word w[4*(Nr+1)];
- KeyExpansion(key, w);
- //Output plaintext to be encrypted
- cout << endl << "Plaintext to be encrypted:"<<endl;
- for(int i=0; i<16; ++i)
- {
- cout << hex << plain[i].to_ulong() << " ";
- if((i+1)%4 == 0)
- cout << endl;
- }
- cout << endl;
- //Encryption, output ciphertext
- encrypt(plain, w);
- cout << "Encrypted ciphertext:"<<endl;
- for(int i=0; i<16; ++i)
- {
- cout << hex << plain[i].to_ulong() << " ";
- if((i+1)%4 == 0)
- cout << endl;
- }
- cout << endl;
- //Decrypt, output plaintext
- decrypt(plain, w);
- cout << "Decrypted plaintext:"<<endl;
- for(int i=0; i<16; ++i)
- {
- cout << hex << plain[i].to_ulong() << " ";
- if((i+1)%4 == 0)
- cout << endl;
- }
- cout << endl;
- return 0;
- }
Screenshots of test results:
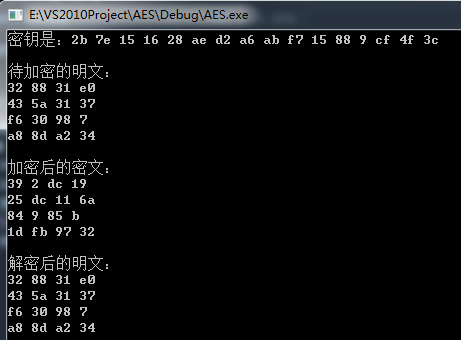
It can be seen that the test results are the same as the expected output, indicating the success of data encryption and decryption!!!
Now let's write AES to encrypt and decrypt files. After encrypting and decrypting 128 bits of data successfully, it's very simple to encrypt and decrypt files. It only needs to read 128 bits at a time. After encrypting, it writes 128 bits of ciphertext to another file. ... so loop until the end of the file. The following is the test code for AES encryption and decryption of a picture (efficiency is neglected, I will optimize it when I have time):
- //#include <fstream>
- typedef bitset<8> byte;
- typedef bitset<32> word;
- /**
- * Converting an array of char characters into binary
- * Save it in a byte array
- */
- void charToByte(byte out[16], const char s[16])
- {
- for(int i=0; i<16; ++i)
- for(int j=0; j<8; ++j)
- out[i][j]= ((s[i]>>j) & 1);
- }
- /**
- * Divide consecutive 128 bits into 16 groups and store them in a byte array
- */
- void divideToByte(byte out[16], bitset<128>& data)
- {
- bitset<128> temp;
- for(int i=0; i<16; ++i)
- {
- temp = (data << 8*i) >> 120;
- out[i] = temp.to_ulong();
- }
- }
- /**
- * Merge 16 byte s into 128 consecutive bits
- */
- bitset<128> mergeByte(byte in[16])
- {
- bitset<128> res;
- res.reset(); //Set 0
- bitset<128> temp;
- for(int i=0; i<16; ++i)
- {
- temp = in[i].to_ulong();
- temp <<= 8*(15-i);
- res |= temp;
- }
- return res;
- }
- int main()
- {
- string keyStr = "abcdefghijklmnop";
- byte key[16];
- charToByte(key, keyStr.c_str());
- //Key expansion
- word w[4*(Nr+1)];
- KeyExpansion(key, w);
- bitset<128> data;
- byte plain[16];
- //Encrypt the file flower.jpg into cipher.txt
- ifstream in;
- ofstream out;
- in.open("D://flower.jpg", ios::binary);
- out.open("D://cipher.txt", ios::binary);
- while(in.read((char*)&data, sizeof(data)))
- {
- divideToByte(plain, data);
- encrypt(plain, w);
- data = mergeByte(plain);
- out.write((char*)&data, sizeof(data));
- data.reset(); //Set 0
- }
- in.close();
- out.close();
- //Decrypt cipher.txt and write the picture flower1.jpg
- in.open("D://cipher.txt", ios::binary);
- out.open("D://flower1.jpg", ios::binary);
- while(in.read((char*)&data, sizeof(data)))
- {
- divideToByte(plain, data);
- decrypt(plain, w);
- data = mergeByte(plain);
- out.write((char*)&data, sizeof(data));
- data.reset(); //Set 0
- }
- in.close();
- out.close();
- return 0;
- }
(End of the text)
Update - December 21, 2014
Multiplication over finite field GF(28) is implemented by table lookup, and the encryption speed of AES is increased by more than 80%. Therefore, table lookup is recommended. The following are six multiplication results tables used in AES algorithm:
- byte Mul_02[256] = {
- 0x00,0x02,0x04,0x06,0x08,0x0a,0x0c,0x0e,0x10,0x12,0x14,0x16,0x18,0x1a,0x1c,0x1e,
- 0x20,0x22,0x24,0x26,0x28,0x2a,0x2c,0x2e,0x30,0x32,0x34,0x36,0x38,0x3a,0x3c,0x3e,
- 0x40,0x42,0x44,0x46,0x48,0x4a,0x4c,0x4e,0x50,0x52,0x54,0x56,0x58,0x5a,0x5c,0x5e,
- 0x60,0x62,0x64,0x66,0x68,0x6a,0x6c,0x6e,0x70,0x72,0x74,0x76,0x78,0x7a,0x7c,0x7e,
- 0x80,0x82,0x84,0x86,0x88,0x8a,0x8c,0x8e,0x90,0x92,0x94,0x96,0x98,0x9a,0x9c,0x9e,
- 0xa0,0xa2,0xa4,0xa6,0xa8,0xaa,0xac,0xae,0xb0,0xb2,0xb4,0xb6,0xb8,0xba,0xbc,0xbe,
- 0xc0,0xc2,0xc4,0xc6,0xc8,0xca,0xcc,0xce,0xd0,0xd2,0xd4,0xd6,0xd8,0xda,0xdc,0xde,
- 0xe0,0xe2,0xe4,0xe6,0xe8,0xea,0xec,0xee,0xf0,0xf2,0xf4,0xf6,0xf8,0xfa,0xfc,0xfe,
- 0x1b,0x19,0x1f,0x1d,0x13,0x11,0x17,0x15,0x0b,0x09,0x0f,0x0d,0x03,0x01,0x07,0x05,
- 0x3b,0x39,0x3f,0x3d,0x33,0x31,0x37,0x35,0x2b,0x29,0x2f,0x2d,0x23,0x21,0x27,0x25,
- 0x5b,0x59,0x5f,0x5d,0x53,0x51,0x57,0x55,0x4b,0x49,0x4f,0x4d,0x43,0x41,0x47,0x45,
- 0x7b,0x79,0x7f,0x7d,0x73,0x71,0x77,0x75,0x6b,0x69,0x6f,0x6d,0x63,0x61,0x67,0x65,
- 0x9b,0x99,0x9f,0x9d,0x93,0x91,0x97,0x95,0x8b,0x89,0x8f,0x8d,0x83,0x81,0x87,0x85,
- 0xbb,0xb9,0xbf,0xbd,0xb3,0xb1,0xb7,0xb5,0xab,0xa9,0xaf,0xad,0xa3,0xa1,0xa7,0xa5,
- 0xdb,0xd9,0xdf,0xdd,0xd3,0xd1,0xd7,0xd5,0xcb,0xc9,0xcf,0xcd,0xc3,0xc1,0xc7,0xc5,
- 0xfb,0xf9,0xff,0xfd,0xf3,0xf1,0xf7,0xf5,0xeb,0xe9,0xef,0xed,0xe3,0xe1,0xe7,0xe5
- };
- byte Mul_03[256] = {
- 0x00,0x03,0x06,0x05,0x0c,0x0f,0x0a,0x09,0x18,0x1b,0x1e,0x1d,0x14,0x17,0x12,0x11,
- 0x30,0x33,0x36,0x35,0x3c,0x3f,0x3a,0x39,0x28,0x2b,0x2e,0x2d,0x24,0x27,0x22,0x21,
- 0x60,0x63,0x66,0x65,0x6c,0x6f,0x6a,0x69,0x78,0x7b,0x7e,0x7d,0x74,0x77,0x72,0x71,
- 0x50,0x53,0x56,0x55,0x5c,0x5f,0x5a,0x59,0x48,0x4b,0x4e,0x4d,0x44,0x47,0x42,0x41,
- 0xc0,0xc3,0xc6,0xc5,0xcc,0xcf,0xca,0xc9,0xd8,0xdb,0xde,0xdd,0xd4,0xd7,0xd2,0xd1,
- 0xf0,0xf3,0xf6,0xf5,0xfc,0xff,0xfa,0xf9,0xe8,0xeb,0xee,0xed,0xe4,0xe7,0xe2,0xe1,
- 0xa0,0xa3,0xa6,0xa5,0xac,0xaf,0xaa,0xa9,0xb8,0xbb,0xbe,0xbd,0xb4,0xb7,0xb2,0xb1,
- 0x90,0x93,0x96,0x95,0x9c,0x9f,0x9a,0x99,0x88,0x8b,0x8e,0x8d,0x84,0x87,0x82,0x81,
- 0x9b,0x98,0x9d,0x9e,0x97,0x94,0x91,0x92,0x83,0x80,0x85,0x86,0x8f,0x8c,0x89,0x8a,
- 0xab,0xa8,0xad,0xae,0xa7,0xa4,0xa1,0xa2,0xb3,0xb0,0xb5,0xb6,0xbf,0xbc,0xb9,0xba,
- 0xfb,0xf8,0xfd,0xfe,0xf7,0xf4,0xf1,0xf2,0xe3,0xe0,0xe5,0xe6,0xef,0xec,0xe9,0xea,
- 0xcb,0xc8,0xcd,0xce,0xc7,0xc4,0xc1,0xc2,0xd3,0xd0,0xd5,0xd6,0xdf,0xdc,0xd9,0xda,
- 0x5b,0x58,0x5d,0x5e,0x57,0x54,0x51,0x52,0x43,0x40,0x45,0x46,0x4f,0x4c,0x49,0x4a,
- 0x6b,0x68,0x6d,0x6e,0x67,0x64,0x61,0x62,0x73,0x70,0x75,0x76,0x7f,0x7c,0x79,0x7a,
- 0x3b,0x38,0x3d,0x3e,0x37,0x34,0x31,0x32,0x23,0x20,0x25,0x26,0x2f,0x2c,0x29,0x2a,
- 0x0b,0x08,0x0d,0x0e,0x07,0x04,0x01,0x02,0x13,0x10,0x15,0x16,0x1f,0x1c,0x19,0x1a
- };
- byte Mul_09[256] = {
- 0x00,0x09,0x12,0x1b,0x24,0x2d,0x36,0x3f,0x48,0x41,0x5a,0x53,0x6c,0x65,0x7e,0x77,
- 0x90,0x99,0x82,0x8b,0xb4,0xbd,0xa6,0xaf,0xd8,0xd1,0xca,0xc3,0xfc,0xf5,0xee,0xe7,
- 0x3b,0x32,0x29,0x20,0x1f,0x16,0x0d,0x04,0x73,0x7a,0x61,0x68,0x57,0x5e,0x45,0x4c,
- 0xab,0xa2,0xb9,0xb0,0x8f,0x86,0x9d,0x94,0xe3,0xea,0xf1,0xf8,0xc7,0xce,0xd5,0xdc,
- 0x76,0x7f,0x64,0x6d,0x52,0x5b,0x40,0x49,0x3e,0x37,0x2c,0x25,0x1a,0x13,0x08,0x01,
- 0xe6,0xef,0xf4,0xfd,0xc2,0xcb,0xd0,0xd9,0xae,0xa7,0xbc,0xb5,0x8a,0x83,0x98,0x91,
- 0x4d,0x44,0x5f,0x56,0x69,0x60,0x7b,0x72,0x05,0x0c,0x17,0x1e,0x21,0x28,0x33,0x3a,
- 0xdd,0xd4,0xcf,0xc6,0xf9,0xf0,0xeb,0xe2,0x95,0x9c,0x87,0x8e,0xb1,0xb8,0xa3,0xaa,
- 0xec,0xe5,0xfe,0xf7,0xc8,0xc1,0xda,0xd3,0xa4,0xad,0xb6,0xbf,0x80,0x89,0x92,0x9b,
- 0x7c,0x75,0x6e,0x67,0x58,0x51,0x4a,0x43,0x34,0x3d,0x26,0x2f,0x10,0x19,0x02,0x0b,
- 0xd7,0xde,0xc5,0xcc,0xf3,0xfa,0xe1,0xe8,0x9f,0x96,0x8d,0x84,0xbb,0xb2,0xa9,0xa0,
- 0x47,0x4e,0x55,0x5c,0x63,0x6a,0x71,0x78,0x0f,0x06,0x1d,0x14,0x2b,0x22,0x39,0x30,
- 0x9a,0x93,0x88,0x81,0xbe,0xb7,0xac,0xa5,0xd2,0xdb,0xc0,0xc9,0xf6,0xff,0xe4,0xed,
- 0x0a,0x03,0x18,0x11,0x2e,0x27,0x3c,0x35,0x42,0x4b,0x50,0x59,0x66,0x6f,0x74,0x7d,
- 0xa1,0xa8,0xb3,0xba,0x85,0x8c,0x97,0x9e,0xe9,0xe0,0xfb,0xf2,0xcd,0xc4,0xdf,0xd6,
- 0x31,0x38,0x23,0x2a,0x15,0x1c,0x07,0x0e,0x79,0x70,0x6b,0x62,0x5d,0x54,0x4f,0x46
- };
- byte Mul_0b[256] = {
- 0x00,0x0b,0x16,0x1d,0x2c,0x27,0x3a,0x31,0x58,0x53,0x4e,0x45,0x74,0x7f,0x62,0x69,
- 0xb0,0xbb,0xa6,0xad,0x9c,0x97,0x8a,0x81,0xe8,0xe3,0xfe,0xf5,0xc4,0xcf,0xd2,0xd9,
- 0x7b,0x70,0x6d,0x66,0x57,0x5c,0x41,0x4a,0x23,0x28,0x35,0x3e,0x0f,0x04,0x19,0x12,
- 0xcb,0xc0,0xdd,0xd6,0xe7,0xec,0xf1,0xfa,0x93,0x98,0x85,0x8e,0xbf,0xb4,0xa9,0xa2,
- 0xf6,0xfd,0xe0,0xeb,0xda,0xd1,0xcc,0xc7,0xae,0xa5,0xb8,0xb3,0x82,0x89,0x94,0x9f,
- 0x46,0x4d,0x50,0x5b,0x6a,0x61,0x7c,0x77,0x1e,0x15,0x08,0x03,0x32,0x39,0x24,0x2f,
- 0x8d,0x86,0x9b,0x90,0xa1,0xaa,0xb7,0xbc,0xd5,0xde,0xc3,0xc8,0xf9,0xf2,0xef,0xe4,
- 0x3d,0x36,0x2b,0x20,0x11,0x1a,0x07,0x0c,0x65,0x6e,0x73,0x78,0x49,0x42,0x5f,0x54,
- 0xf7,0xfc,0xe1,0xea,0xdb,0xd0,0xcd,0xc6,0xaf,0xa4,0xb9,0xb2,0x83,0x88,0x95,0x9e,
- 0x47,0x4c,0x51,0x5a,0x6b,0x60,0x7d,0x76,0x1f,0x14,0x09,0x02,0x33,0x38,0x25,0x2e,
- 0x8c,0x87,0x9a,0x91,0xa0,0xab,0xb6,0xbd,0xd4,0xdf,0xc2,0xc9,0xf8,0xf3,0xee,0xe5,
- 0x3c,0x37,0x2a,0x21,0x10,0x1b,0x06,0x0d,0x64,0x6f,0x72,0x79,0x48,0x43,0x5e,0x55,
- 0x01,0x0a,0x17,0x1c,0x2d,0x26,0x3b,0x30,0x59,0x52,0x4f,0x44,0x75,0x7e,0x63,0x68,
- 0xb1,0xba,0xa7,0xac,0x9d,0x96,0x8b,0x80,0xe9,0xe2,0xff,0xf4,0xc5,0xce,0xd3,0xd8,
- 0x7a,0x71,0x6c,0x67,0x56,0x5d,0x40,0x4b,0x22,0x29,0x34,0x3f,0x0e,0x05,0x18,0x13,
- 0xca,0xc1,0xdc,0xd7,0xe6,0xed,0xf0,0xfb,0x92,0x99,0x84,0x8f,0xbe,0xb5,0xa8,0xa3
- };
- byte Mul_0d[256] = {
- 0x00,0x0d,0x1a,0x17,0x34,0x39,0x2e,0x23,0x68,0x65,0x72,0x7f,0x5c,0x51,0x46,0x4b,
- 0xd0,0xdd,0xca,0xc7,0xe4,0xe9,0xfe,0xf3,0xb8,0xb5,0xa2,0xaf,0x8c,0x81,0x96,0x9b,
- 0xbb,0xb6,0xa1,0xac,0x8f,0x82,0x95,0x98,0xd3,0xde,0xc9,0xc4,0xe7,0xea,0xfd,0xf0,
- 0x6b,0x66,0x71,0x7c,0x5f,0x52,0x45,0x48,0x03,0x0e,0x19,0x14,0x37,0x3a,0x2d,0x20,
- 0x6d,0x60,0x77,0x7a,0x59,0x54,0x43,0x4e,0x05,0x08,0x1f,0x12,0x31,0x3c,0x2b,0x26,
- 0xbd,0xb0,0xa7,0xaa,0x89,0x84,0x93,0x9e,0xd5,0xd8,0xcf,0xc2,0xe1,0xec,0xfb,0xf6,
- 0xd6,0xdb,0xcc,0xc1,0xe2,0xef,0xf8,0xf5,0xbe,0xb3,0xa4,0xa9,0x8a,0x87,0x90,0x9d,
- 0x06,0x0b,0x1c,0x11,0x32,0x3f,0x28,0x25,0x6e,0x63,0x74,0x79,0x5a,0x57,0x40,0x4d,
- 0xda,0xd7,0xc0,0xcd,0xee,0xe3,0xf4,0xf9,0xb2,0xbf,0xa8,0xa5,0x86,0x8b,0x9c,0x91,
- 0x0a,0x07,0x10,0x1d,0x3e,0x33,0x24,0x29,0x62,0x6f,0x78,0x75,0x56,0x5b,0x4c,0x41,
- 0x61,0x6c,0x7b,0x76,0x55,0x58,0x4f,0x42,0x09,0x04,0x13,0x1e,0x3d,0x30,0x27,0x2a,
- 0xb1,0xbc,0xab,0xa6,0x85,0x88,0x9f,0x92,0xd9,0xd4,0xc3,0xce,0xed,0xe0,0xf7,0xfa,
- 0xb7,0xba,0xad,0xa0,0x83,0x8e,0x99,0x94,0xdf,0xd2,0xc5,0xc8,0xeb,0xe6,0xf1,0xfc,
- 0x67,0x6a,0x7d,0x70,0x53,0x5e,0x49,0x44,0x0f,0x02,0x15,0x18,0x3b,0x36,0x21,0x2c,
- 0x0c,0x01,0x16,0x1b,0x38,0x35,0x22,0x2f,0x64,0x69,0x7e,0x73,0x50,0x5d,0x4a,0x47,
- 0xdc,0xd1,0xc6,0xcb,0xe8,0xe5,0xf2,0xff,0xb4,0xb9,0xae,0xa3,0x80,0x8d,0x9a,0x97
- };
- byte Mul_0e[256] = {
- 0x00,0x0e,0x1c,0x12,0x38,0x36,0x24,0x2a,0x70,0x7e,0x6c,0x62,0x48,0x46,0x54,0x5a,
- 0xe0,0xee,0xfc,0xf2,0xd8,0xd6,0xc4,0xca,0x90,0x9e,0x8c,0x82,0xa8,0xa6,0xb4,0xba,
- 0xdb,0xd5,0xc7,0xc9,0xe3,0xed,0xff,0xf1,0xab,0xa5,0xb7,0xb9,0x93,0x9d,0x8f,0x81,
- 0x3b,0x35,0x27,0x29,0x03,0x0d,0x1f,0x11,0x4b,0x45,0x57,0x59,0x73,0x7d,0x6f,0x61,
- 0xad,0xa3,0xb1,0xbf,0x95,0x9b,0x89,0x87,0xdd,0xd3,0xc1,0xcf,0xe5,0xeb,0xf9,0xf7,
- 0x4d,0x43,0x51,0x5f,0x75,0x7b,0x69,0x67,0x3d,0x33,0x21,0x2f,0x05,0x0b,0x19,0x17,
- 0x76,0x78,0x6a,0x64,0x4e,0x40,0x52,0x5c,0x06,0x08,0x1a,0x14,0x3e,0x30,0x22,0x2c,
- 0x96,0x98,0x8a,0x84,0xae,0xa0,0xb2,0xbc,0xe6,0xe8,0xfa,0xf4,0xde,0xd0,0xc2,0xcc,
- 0x41,0x4f,0x5d,0x53,0x79,0x77,0x65,0x6b,0x31,0x3f,0x2d,0x23,0x09,0x07,0x15,0x1b,
- 0xa1,0xaf,0xbd,0xb3,0x99,0x97,0x85,0x8b,0xd1,0xdf,0xcd,0xc3,0xe9,0xe7,0xf5,0xfb,
- 0x9a,0x94,0x86,0x88,0xa2,0xac,0xbe,0xb0,0xea,0xe4,0xf6,0xf8,0xd2,0xdc,0xce,0xc0,
- 0x7a,0x74,0x66,0x68,0x42,0x4c,0x5e,0x50,0x0a,0x04,0x16,0x18,0x32,0x3c,0x2e,0x20,
- 0xec,0xe2,0xf0,0xfe,0xd4,0xda,0xc8,0xc6,0x9c,0x92,0x80,0x8e,0xa4,0xaa,0xb8,0xb6,
- 0x0c,0x02,0x10,0x1e,0x34,0x3a,0x28,0x26,0x7c,0x72,0x60,0x6e,0x44,0x4a,0x58,0x56,
- 0x37,0x39,0x2b,0x25,0x0f,0x01,0x13,0x1d,0x47,0x49,0x5b,0x55,0x7f,0x71,0x63,0x6d,
- 0xd7,0xd9,0xcb,0xc5,0xef,0xe1,0xf3,0xfd,0xa7,0xa9,0xbb,0xb5,0x9f,0x91,0x83,0x8d
- };