C++ High Precision Algorithms

Keywords: less

The complete template is at the end! First came the explanation.

Introduction of High Precision Algorithms

In C++ when you use super-huge numbers that int, long, or even unsigned long cannot handle, you will feel extremely painful or even desperate, so we have only one method at this time - high-precision algorithm.

High-precision algorithm: belongs to the mathematical calculation method of processing large numbers. It is an analog addition, subtraction, multiplication and division operation for super-large data by computer. For very large numbers can not be stored properly in the computer, so the number is split into bits and stored in an array, using an array to represent a number, so that the number is called a high-precision number.

High Precision Structural Body Solution Method

Here, we will save each high-precision number as a structure called BigInt. There are two main variables: (PS: Make sure you have mastered the structure)
1) num [] is responsible for recording each digit (num[1] represents a bit, num[2] represents ten bits, num[3] represents a hundred bits...).
2) len is responsible for recording the number of digits.

Here M is the upper limit of this number.

PS: static int x is to let all high-precision numbers share this variable. For example, if I change this quantity in the first high-precision number, then I change this quantity in the remaining high-precision numbers. It can be regarded as a global variable, but it can only be used in this structure. In order to optimize the space and make BigInt structure independent.

Next, we give an initial value of 0 and construct a zero-clearing function together.

Read-in idea: first read in by character array, and then put it upside down into int array.

Output thinking: backward output.

Comparing Operational Thoughts (Take Less Than Number as an Example):
1) Comparing digit len.
2) Comparing one num to another.
3) Not yet. It's equal.

Additive thinking: One by one add, and then carry.
Let S.num[i] += num[i] + A.num[i]; (remember that it must be +=, because S.num[i] may change to 1 due to the carry of the previous position).
Then it is judged that if S.num[i] is a two-digit number, that is, greater than or equal to 10, carry: let S.num[i] -= 10, S.num[i + 1]+.

Subtraction thinking: one by one subtraction, and then borrow.
Let S.num[i] += num[i] - A.num[i];
Then, if S.num[i] is less than 0, borrow 1 from the higher one: let S.num[i] += 10, S.num[i + 1] -.

Multiplication thinking: one by one to multiply, then carry
Suppose you multiply the position i of this by the position j of A:
For example, the conditions are as follows.
It is known that this.num[5] * A.num[3] is added to the seventh position, that is (3 + 5 - 1).
It is deduced that this.num[i] * A.num[j] is added to the position (i + j - 1).

So let S.num[i + j - 1] += num[i] * A.num[j], and then carry on.

Dividing thinking: column vertical.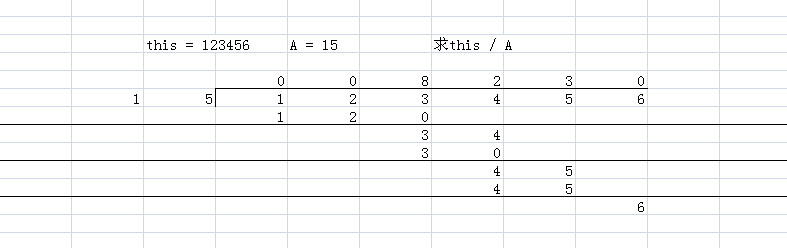

You can understand it in terms of the pictures above and in combination with the words.
Open a new number R = 0, let it record the current surplus, add a num[i] (R = R * 10 + num[i]) at the end of each R, and then remove it with R at this time. The trademark of A.num[i] is S.num[i], and the remainder covers R and goes on cycling. Finally, turn S into OK as a whole! (Apparently too brief)

Remaining idea: Because the result after division is taken as a whole, let S = this - (this / A) * A be OK.

Next comes the structured code.

# include <cstdio>
# include <iostream>
# include <cstring>
# include <algorithm>
# include <cmath>

using namespace std;

# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)

struct BigInt
{
    static const int M = 10000;
    int num[M + 10], len;

    BigInt() { clean(); }	

	void clean(){
    	memset(num, 0, sizeof(num));
    	len = 1;
	}

    void read(){
    	char str[M + 10];
        scanf("%s", str);
        len = strlen(str);
        FOR(i, 1, len)
            num[i] = str[len - i] - '0';
    }

    void write(){
        _FOR(i, len, 1)
            printf("%d", num[i]);
        puts("");
    }
    
    void itoBig(int x){
    	clean();
    	while(x != 0){
    		num[len++] = x % 10;
    		x /= 10;
		}
		if(len != 1) len--;
	}

    bool operator < (const BigInt &cmp) const {
        if(len != cmp.len) return len < cmp.len;
        _FOR(i, len, 1)
            if(num[i] != cmp.num[i]) return num[i] < cmp.num[i];
        return false;
    }

    bool operator > (const BigInt &cmp) const { return cmp < *this; }
	bool operator <= (const BigInt &cmp) const { return !(cmp < *this); }
	bool operator != (const BigInt &cmp) const { return cmp < *this || *this < cmp; }
	bool operator == (const BigInt &cmp) const { return !(cmp < *this || *this < cmp); }

    BigInt operator + (const BigInt &A) const {
        BigInt S;
        S.len = max(len, A.len);
        FOR(i, 1, S.len){
            S.num[i] += num[i] + A.num[i];
            if(S.num[i] >= 10){
                S.num[i] -= 10;
                S.num[i + 1]++;
            }
        }
        while(S.num[S.len + 1]) S.len++;
        return S;
    }

    BigInt operator - (const BigInt &A) const {
        BigInt S;
        S.len = max(len, A.len);
        FOR(i, 1, S.len){
            S.num[i] += num[i] - A.num[i];
            if(S.num[i] < 0){
                S.num[i] += 10;
                S.num[i + 1]--;
            }
        }
        while(!S.num[S.len] && S.len > 1) S.len--;
        return S;
    }

    BigInt operator * (const BigInt &A) const {
        BigInt S;
        if((A.len == 1 && A.num[1] == 0) || (len == 1 && num[1] == 0)) return S;
        S.len = A.len + len - 1;
        FOR(i, 1, len)
            FOR(j, 1, A.len){
                S.num[i + j - 1] += num[i] * A.num[j];
                S.num[i + j] += S.num[i + j - 1] / 10;
                S.num[i + j - 1] %= 10;
            }
        while(S.num[S.len + 1]) S.len++;
        return S;
    }

    BigInt operator / (const BigInt &A) const {
        BigInt S;
        if((A.len == 1 && A.num[1] == 0) || (len == 1 && num[1] == 0)) return S;
        BigInt R, N;
        S.len = 0; 
        _FOR(i, len, 1){
        	N.itoBig(10);
			R = R * N;
			N.itoBig(num[i]);
			R = R + N;
        	int flag = -1;
        	FOR(j, 1, 10){
        		N.itoBig(j);
        		if(N * A > R){
        			flag = j - 1;
        			break;
				}
			}
			S.num[++S.len] = flag;
			N.itoBig(flag);
			R = R - N * A;
		}
		FOR(i, 1, S.len / 2) swap(S.num[i], S.num[len - i + 1]);
		while(!S.num[S.len] && S.len > 1) S.len--;
        return S;
    }
    
    BigInt operator % (const BigInt &A) const {
    	BigInt S;
    	BigInt P = *this / A;
    	S = *this - P * A;
    	return S;
    }
};

int main()
{
	return 0;
}

High Precision Functional Solution

The idea is roughly the same as above, but this time we use string to write some functions.
(PS: The beginning NR is the upper limit of digits)

Functional code.

# include <cstdio>
# include <iostream>
# include <cstring>
# include <algorithm>
# include <cmath>

using namespace std;

# define FOR(i, a, b) for(int i = a; i <= b; i++)
# define _FOR(i, a, b) for(int i = a; i >= b; i--)

const int NR = 10000;

bool STRcompare(string str1, string str2){
	int len1 = str1.size(), len2 = str2.size();
    if(len1 != len2) return len1 < len2;
    FOR(i, 0, len1 - 1)
        if(str1[i] != str2[i]) return str1[i] < str2[i];
    return false;
}

string STRaddition(string str1, string str2){
    int sum[NR + 10], a[NR + 10], b[NR + 10];
    memset(sum, 0, sizeof(sum));
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    int len1 = str1.size(), len2 = str2.size();
    FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
    FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
    int lenS = max(len1, len2);
    FOR(i, 1, lenS){
        sum[i] += a[i] + b[i];
    	if(sum[i] >= 10){
            sum[i] -= 10;
            sum[i + 1]++;
    	}
    }
    while(sum[lenS + 1]) lenS++;
    string ans;
    _FOR(i, lenS, 1) ans += sum[i] + '0';
    return ans;
}

string STRsubtraction(string str1, string str2){
    int sum[NR + 10], a[NR + 10], b[NR + 10];
    memset(sum, 0, sizeof(sum));
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    if(STRcompare(str1, str2)) swap(str1, str2);
    int len1 = str1.size(), len2 = str2.size();
    FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
    FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
    int lenS = max(len1, len2);
    FOR(i, 1, lenS){
        sum[i] += a[i] - b[i];
    	if(sum[i] < 0){
            sum[i] += 10;
            sum[i + 1]--;
    	}
    }
    while(sum[lenS] == 0 && lenS > 1) lenS--;
    string ans;
    _FOR(i, lenS, 1) ans += sum[i] + '0';
    return ans;
}    

string STRmultiplication(string str1, string str2){
	if(str1.size() == 1 && str1[0] == '0') return str1;
	if(str2.size() == 1 && str2[0] == '0') return str2;
	int sum[NR + 10], a[NR + 10], b[NR + 10];
    memset(sum, 0, sizeof(sum));
    memset(a, 0, sizeof(a));
    memset(b, 0, sizeof(b));
    int len1 = str1.size(), len2 = str2.size();
    FOR(i, 1, len1) a[i] = str1[len1 - i] - '0';
    FOR(i, 1, len2) b[i] = str2[len2 - i] - '0';
    int lenS = len1 + len2 - 1;
    FOR(i, 1, len1)
        FOR(j, 1, len2){
            sum[i + j - 1] += a[i] * b[j];
            sum[i + j] += sum[i + j - 1] / 10;
        	sum[i + j - 1] %= 10;
        }
    while(sum[lenS + 1]) lenS++;
    string ans;
    _FOR(i, lenS, 1) ans += sum[i] + '0';
    return ans;
}

string char_to_string(char c){
	string str;
	str += c;
	return str;
}

string int_to_string(int x){
	int a[NR + 10], len = 0;
	while(x != 0){
		a[++len] = x % 10;
		x /= 10;
	}
	string str;
	_FOR(i, len, 1) str += a[i] + '0';
	if(len == 0) str = "0";
	return str;
}

string STRdivision(string str1, string str2){
    if(str1.size() == 1 && str1[0] == '0') return str1;
	if(str2.size() == 1 && str2[0] == '0') return str2;
	if(STRcompare(str1, str2)) swap(str1, str2);
	string R = "0", ans;
	bool not_zero = false;
    FOR(i, 0, str1.size() - 1){
		R = STRaddition(STRmultiplication(R, "10"), char_to_string(str1[i]));
        int flag = -1;
        FOR(j, 1, 10)
        	if(STRcompare(R, STRmultiplication(int_to_string(j), str2))){
        		flag = j - 1;
        		break;
			}
		if(flag != 0 || not_zero){
			ans += flag + '0';
			not_zero = true;
		}
		R = STRsubtraction(R, STRmultiplication(int_to_string(flag), str2));
	}
    return ans;
}

string STRremainder(string str1, string str2){
	if(str1.size() == 1 && str1[0] == '0') return str1;
	if(str2.size() == 1 && str2[0] == '0') return str2;
	if(STRcompare(str1, str2)) swap(str1, str2);
    string P = STRdivision(str1, str2);
    string ans = STRsubtraction(str1, STRmultiplication(P, str2));
    return ans;
};

int main()
{
	return 0;
}

Practice

See if you have a high-precision algorithm? Do an exercise and practice your hands.

1) P1601 A+B Problem (high precision): https://www.luogu.org/problemnew/show/P1601
2) P2142 high precision subtraction: https://www.luogu.org/problemnew/show/P2142
3) P1080 King Game: https://www.luogu.org/problemnew/show/P1080

High-precision algorithms are here today, but there are more operations such as square, multiplier, factorial.
If you are interested in writing by yourself, there is no more to say here.

God Bless You For Ever!

Posted by exnet on Mon, 12 Aug 2019 23:35:39 -0700

Programmer Group

C++ High Precision Algorithms

Introduction of High Precision Algorithms

High Precision Structural Body Solution Method

High Precision Functional Solution

Practice

Hot Keywords