What is high precision operation?

In fact, high precision means that the range of data and results involved in the operation is beyond the range of data size that can be represented by standard data types. At this time, if we want to get the correct calculation results, obviously we can not rely on the ordinary method to achieve. On the basis of general operation principle, auxiliary algorithm is used to realize the calculation of super-large data. For example, find the sum of two 100-bit data, or calculate the product of two 100-bit numbers. High-precision algorithms will be used at this time.

High plus:

Thoughts

1. Since the arithmetic number exceeds the range of data size, we choose to store the number in an array.
2. Store the array in reverse order to facilitate the addition operation
3. Print the array in reverse order after the operation is completed (so it looks sequential)

The code is as follows:

#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

//Nomenclature of Structural Weight
typedef struct {
	char data[1000];//1000-bit high-quality (self-expanding)
	int len;		//How long is the number?
}HighAcc;

//Inverse Array and Convert Characters to Numbers
void dealNumber(HighAcc *h){
	int start = 0, end = strlen(h->data) - 1;
	char tmp;

	h->len = end + 1;//Calculating the Length of Arrays in Structures
	for (; start <= end; start++, end--){//Complete Digital Inverse Sequence Storage
		tmp = h->data[start];
		h->data[start] = h->data[end] - '0';//Converting Characters to Numbers
		h->data[end] = tmp - '0';
	}
}

//High Precision Addition
HighAcc add(HighAcc m_num1, HighAcc m_num2){
	HighAcc sum = { 0 };
	int i, tmp;
	
	//Length of storing longer arrays
	int maxlen = m_num1.len >= m_num2.len ? m_num1.len : m_num2.len;

	for (i = 0; i < maxlen; i++){//High Precision Addition Algorithms
		tmp = m_num1.data[i] + m_num2.data[i] + sum.data[i];
		sum.data[i] = tmp % 10;//Get the number of each bit.
		sum.data[i + 1] = tmp / 10;//Judging the number of high digits
	}
	sum.len = maxlen + sum.data[maxlen];//Get the length of sum
	return sum;
}

//Array Reverse Printing
void printNumber(HighAcc h){
	int i;
	for (i = h.len - 1; i >= 0; i--){
		putchar(h.data[i] + '0');	//Converting Numbers to Characters
	}
}

int main(){
	HighAcc num1 = { 0 };
	HighAcc num2 = { 0 };
	HighAcc sum;

	scanf("%s%s", num1.data, num2.data);

	dealNumber(&num1);
	dealNumber(&num2);

	sum = add(num1, num2);

	printNumber(sum);
	putchar('\n');

	system("pause");
	return 0;
}

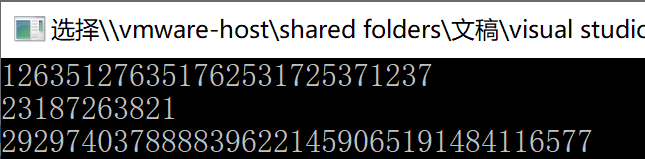
Code generation diagram:

High precision multiplication:

The realization principle of high-precision multiplication:

• High-precision multiplier only needs to change some algorithms on the basis of high-precision multiplier, so write them in a blog.

The code is as follows:

#define _CRT_SECURE_NO_WARNINGS

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

//Nomenclature of Structural Weight
typedef struct {
	char data[1000];//1,000-digit Excellence
	int len;		//How long is the number?
}HighAcc;

//Digital Inverse Sequence Storage (Array Multiplied Left to Right)
void dealNumber(HighAcc *h){
	int start = 0, end = strlen(h->data) - 1;
	char tmp;

	h->len = end + 1;//Calculating the Length of Arrays in Structures
	for (; start <= end; start++, end--){//Complete Inverse Array Storage
		tmp = h->data[start];
		h->data[start] = h->data[end] - '0';//To convert characters into numbers
		h->data[end] = tmp - '0';
	}
}

//Numbers are printed in reverse order (which seems to be the order)
void printNumber(HighAcc h){
	int i;
	for (i = h.len - 1; i >= 0; i--){
		putchar(h.data[i] + '0');	//Converting Numbers to Characters
	}
}

//High Precision Multiplication Algorithms
HighAcc mul(HighAcc m_num1, HighAcc m_num2){
	HighAcc sum = { 0 };
	int i, j, tmp;
	
	//If one of them is 0, return 0 directly.
	if ((m_num1.len == 1 && m_num1.data[0] == 0) || (m_num2.len == 1 && m_num2.data[0] == 0)){
		sum.len = 1;
		return sum;
	}

//The Core of High Precision Multiplication Algorithms
	for (i = 0; i < m_num1.len; i++){
		for (j = 0; j < m_num2.len; j++){
			tmp = m_num1.data[i] * m_num2.data[j] + sum.data[i + j];
			sum.data[i + j] = tmp % 10;
			sum.data[i + j + 1] += tmp / 10;
		}
	}
	sum.len = m_num1.len + m_num2.len - !sum.data[m_num1.len + m_num2.len - 1];//Get the length of sum
	return sum;
}

int main(){
	HighAcc num1 = { 0 };
	HighAcc num2 = { 0 };
	HighAcc sum;

	scanf("%s%s", num1.data, num2.data);

	dealNumber(&num1);
	dealNumber(&num2);

	sum = mul(num1, num2);

	printNumber(sum);
	putchar('\n');

	system("pause");
	return 0;
}

Code generation diagram: