Binary Search

introduce

Binary search, also known as half search, logarithmic search.Is an algorithm used to find a number in an ordered array.

Example

Title Description

Given an ordered ascending integer array of n elements, nums, and a target value, write a function to search for the target in nums, and return -1 if the target value has a return subscript, otherwise it returns -1.

Example 1:

input: nums = [-1,0,3,5,9,12], target = 9
 output: 4
 explain: 9 Appears in nums Medium and subscript 4

Example 2:

input: nums = [-1,0,3,5,9,12], target = 2
 output: -1
 explain: 2 Non-existent nums So return -1

Tips:

1. You can assume n u m s nums All elements in nums are not duplicated.
2. n n n will be in [ 1 , 10000 ] [1, 10000] Between [1,10000].
3. n u m s nums Each element of nums will be in the [ − 9999 , 9999 ] [-9999, 9999] Between [9999,9999].

Solving problems

Idea 1: Violence ( O ( n ) ) (O(n)) (O(n))

Traversing through an array returns its subscript if a target value appears, or -1 if a target value does not appear after traversal because the entire array needs to be traversed once, so the time complexity is O ( n ) O(n) O(n).

Code

class Solution {
public:
    int search(vector<int>& nums, int target) {
        for(int i = 0; i < nums.size(); i ++) // foreach
            if(nums[i] == target) return i; // Returns the subscript if a target value appears
        return -1; // No target value appears after traversal, return -1
    }
};

Idea 2: Dichotomy ( O ( l o g n ) ) (O(logn)) (O(logn))

From the title, we find that the array is ordered and meets the conditions for binary search.Assuming the length of the array is n, we can look at nums[n/2]. If nums[n/2] > target, that means all numbers after nums[n/2] are larger than target. We just need to start with 0 ∼ n / 2 0 \sim n / 2 Find the target in 0_n/2.Otherwise we will start with n / 2 ∼ n − 1 n / 2 \sim n - 1 n/2_n_1 to find, when only the last element is left, we determine if it is equal to the target, and if it is equal, the subscript is returned, otherwise the -1 is returned. Because we only use the first half or the second half of the array each time, and the length of the last array changes from n to 1, the total number of operations k Matches 2 k = n 2^k = n 2k=n, so k = logn, time complexity is O ( l o g n ) O(logn) O(logn).

Code

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int l = 0,r = nums.size() - 1; // Set l as the left boundary and R as the right boundary to find target from nums[]l~r]
        while(l < r){ // If more than one element is left, continue searching
            int mid = l + r >> 1; // Find the midpoint of l~r
            if(nums[mid] < target) l = mid + 1; // If the midpoint value is less than target, look for target from nums[mid + 1,r]
            else r = mid; // Otherwise, find target from nums[l,mid]
        }

        if(nums[l] == target) return l; // Returns the subscript if the remaining number== target
        return -1;// Otherwise return -1
    }
};

Dichotomous thought

The preceding example should have given you a preliminary idea of dichotomy.Is to divide an ordered array into two halves, half of which are elements < = m i d <=mid <=mid value, the other half is the opposite, so only half is what we might need, and the other half can be discarded directly.Generally speaking, not only can sorted arrays be divided into two parts, so long as the left and right sides have different properties, they can be divided. In sorted arrays, the number on the left side of mid is <=mid, and the number on the right side of mid is >=mid. This is the different nature of the left and right sides, which allows us to split the array in half.for example Search Rotated Sort Array Although the array of this topic is not strictly ordered, it can still be answered by dichotomy.

Boundary problem

There is a boundary problem with integer dichotomy, that is, if (nums[mid] < target) l = mid + 1;If we have one from 1 ∼ 100 1 \sim 100 The program code for guessing the number target = 7 in 1_100 is as follows:

#include <iostream>
using namespace std;

int main(){
    int n =100;
    int target = 7;
    int l = 1,r = 100;
    while(l < r){
        cout << l << ' ' << r << endl; // Output l and r
        int mid = l + r >> 1;
        if(mid < target) l = mid;
        else r = mid;
    }

    cout << l;

    return 0;
}

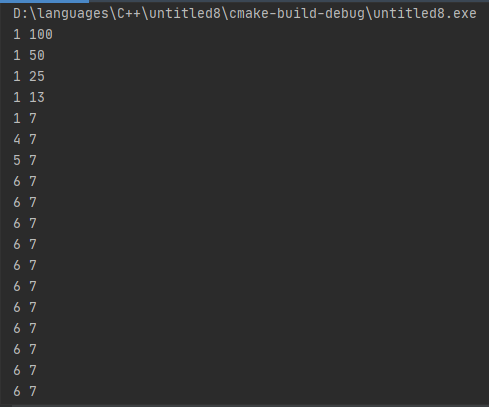
It is easy to see that the program is trapped in a dead loop because when l = 6,r = 7, mid = L + R > > > 1 = 6, 6 < 7, so l = mid = 6, so l = mid = 6, so it is trapped in a dead loop, ultimately because mid = L + R > 1 is rounded down, so it is possible that l and mid are equal when there are two elements left, so making L = mid causes a dead loop.So l = mid + 1 cannot be modified to L = mid in this code, and other situations can be explored freely.