The algorithm sort in STL can be used to sort vector s and deque s, and it needs the support of random access iterators. Because list does not support random access iterators, the list container cannot be sorted by the algorithm sort. Therefore, the list container introduces the sort member function to complete the sorting.
Use of list sort insertion function
#include <iostream>
#include <stdlib.h>
#include <list>
#include <algorithm>
using namespace std;
class A{
private: int n;
public:
A(int _n){
n = _n;
}
friend bool operator < (const A &a1, const A &a2);
friend bool operator ==(const A &a1, const A &a2);
friend ostream& operator << (ostream& o, const A &a2);
};
bool operator <(const A &a1, const A &a2)
{
return a1.n < a2.n;
}
bool operator ==(const A &a1, const A &a2)
{
return a1.n == a2.n;
}
ostream& operator <<(ostream &o, const A &a)
{
o << a.n;
return o;
}
template <class T>
void Print(T first, T last)
{
for (; first != last; ++first)
{
cout << *first << " ";
}
cout << endl;
}
int main()
{
A a[] = { 1, 2, 3, 4, 53, 2 };
A b[] = { 10, 23, 4, 65,23,10,10,10,4,4,7,7,7,87 };
list<A>lst1(a, a + sizeof(a) / sizeof(a[0]))
, lst2(b, b + sizeof(b) / sizeof(b[0]));
lst1.sort();
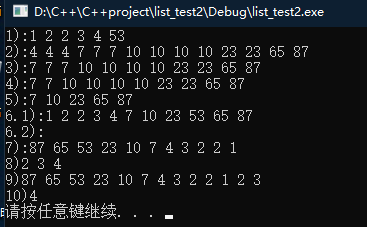
cout << "1):"; Print(lst1.begin(),lst1.end()); //Output after sorting from small to large
lst2.sort();
cout << "2):"; Print(lst2.begin(), lst2.end()); //Output after sorting from small to large
lst2.remove(4); //Delete the same elements as 4
cout << "3):"; Print(lst2.begin(), lst2.end());
lst2.pop_front(); //Delete the first element of lst2
cout << "4):"; Print(lst2.begin(), lst2.end());
lst2.unique(); //Delete all elements equal to the previous element
cout << "5):"; Print(lst2.begin(),lst2.end());
lst1.merge(lst2); //Merge lst2 to lst1 and clear lst2
cout << "6.1):"; Print(lst1.begin(), lst1.end());
cout << "6.2):"; Print(lst2.begin(), lst2.end());
lst1.reverse(); //Inversion of lst1
cout << "7):"; Print(lst1.begin(), lst1.end());
lst2.insert(lst2.begin(), a + 1, a + 4); //Insert three elements into lst2
cout << "8)"; Print(lst2.begin(), lst2.end());
list <A>::iterator p1, p2, p3;
p1 = find(lst1.begin(), lst1.end(), 30);
p2 = find(lst2.begin(), lst2.end(), 2);
p3 = find(lst2.begin(), lst2.end(), 4);
lst1.splice(p1, lst2, p2, p3); //Before inserting [p2, p3] into p1, delete [p2, p3] from lst2
cout << "9)"; Print(lst1.begin(), lst1.end());
cout << "10)"; Print(lst2.begin(), lst2.end());
system("pause");
return 0;
}
Use list to solve Joseph's problem.
Joseph's problem is that there are n monkeys in a clockwise circle to select the king (numbered 1-n), counting from No. 1 to m, counting to m, the monkeys retreat to outside the circle, and the remaining monkeys report from 1. In this way, until there is only one monkey left in the circle, the monkey is the monkey king. After inputting N and m into the program, the number of the last Monkey King is output.
Input data: Each line is two integers separated by spaces, the first is n, and the second is m (0 < m, n <= 1 000 000 000). The last line is:
0 0
Output requirements: For each line of input data (except the last line), the output data is also a line, that is, the number of the last monkey king.
Input sample:
6 2
12 4
8 3
0 0
Output sample:
5
1
7
#include <list>
#include <iostream>
using namespace std;
int main()
{
list<int> monkeys;
int n, m;
while (true) {
cin >> n >> m;
if (n == 0 && m == 0)
break;
monkeys.clear(); //Empty list container
for (int i = 1; i <= n; ++i) //Put the number of the monkey in the list
monkeys.push_back(i);
list<int>::iterator it = monkeys.begin();
while (monkeys.size() > 1) { //As long as there are more than one monkey, we need to find a monkey to let it out.
for (int i = 1; i < m; ++i) { //Number off
++it;
if (it == monkeys.end())
it = monkeys.begin();
}
it = monkeys.erase(it); //After deleting the element, the iterator fails.
//To redirect the iterator to the back of the deleted element
if (it == monkeys.end())
it = monkeys.begin();
}
cout << monkeys.front() << endl; //front returns a reference to the first element
}
return 0;
}
The Difference between vector and list
vector list
The underlying structure is a dynamic sequential list, a continuous space, a bi-directional cyclic list of leading nodes
Random Access Supports Random Access, the Efficiency of Accessing an Element O(1). Random Access Supports Random Access, and the Efficiency of Accessing an Element O(N)
Insertion and deletion at any location is inefficient and requires element removal.
The time complexity is O(N). It may need to be compatible when inserting. The insertion and deletion at any location are efficient and do not need to move elements.
Increase capacity: Open up new space, copy elements, release old space, resulting in lower efficiency.Time complexity O(1)
Space utilization: The bottom is continuous space, which is not easy to cause memory fragmentation, and space utilization. The bottom nodes are opened dynamically, and the small nodes are easy.
High Cache Utilization, High Cache Utilization, Cache Fragmentation, Low Space Utilization and Low Cache Utilization
Iterator, primitive ecological pointer, node pointer, encapsulation of primitive ecological pointer
Iterator failure. When inserting elements, all iterators are reassigned, because inserting elements does not cause iterator failure.
Elements may lead to re-expansion, invalidation of the original iterator, deletion, deletion of elements will only lead to the current iteration
Except when the current iterator needs to be reassigned, otherwise it will fail. The other iterators will not be affected.
Use scenarios need efficient storage, support random access, do not care about insertion and deletion efficiency, a large number of insertion and deletion operations, do not care about random access