In C++, data is input and output in decimal by default.If octal or hexadecimal input and output are required, the corresponding data form must be specified in cin or cout, oct is octal, hex is hexadecimal, and dec is decimal.However, binary has no default output format and needs to write its own function to convert.

Enter the integer n, then in C+, cout < hex < n; cout < OCT < n; cout < Dec < n; the integer n is output in hexadecimal, octal, and decimal formats, respectively

Code annotation

#include <iostream>
#include <bitset>
 
using namespace std;
 
int main(void)
{
	int i,j,k,l;
	cout<<"Input i(oct),j(hex),k(hex),l(dec):"<<endl;
	cin>>oct>>i;  //Input is octal
	cin>>hex>>j;  //Input is hexadecimal
	cin>>k;   //Input is still hexadecimal
	cin>>dec>>l; //Enter as decimal number
	cout<<"hex:"<<"i = "<<hex<<i<<endl;
	cout<<"dec:"<<"j = "<<dec<<j<<'\t'<<"k = "<<k<<endl;
	cout<<"oct:"<<"l = "<<oct<<l;
	cout<<dec<<endl;  //Restore decimal number output state
	return (0);
}

Debug Run

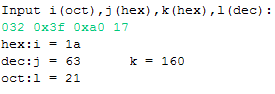
Think and Tip

1. When receiving input, the number system must be specified in cin, otherwise the 0 and 0x flags at the beginning of octal and hexadecimal digits are not recognized when entering from the keyboard.Omit the 0 and 0x flags when specified.

2. Binary control only applies to integer variables, not real and character variables.

3. The format, number and type of input data must correspond to the variables in cin one-to-one, otherwise not only will the input data be incorrect, but also will affect the correct input of other subsequent data.

4.) When a number system is specified in cin or cout, it will remain valid until another number system is re-specified.

The following is a summary of binary output in C++.

Code Notes

#include <iostream>
#include <list>
#include <bitset>
#include <iomanip>
 
using namespace std;
 
//Recursive Output Binary Function
void BinaryRecursion(int n)
{
	int a;
	a = n % 2; // Remaining
	n = n >> 1;  //To move one bit to the right is equivalent to dividing by two
	if(0 != n)
	{
		BinaryRecursion(n);
	}
	cout<<a;
}
 
//Converting binaries using containers
void BinaryVector(int n)
{
	int temp;
	temp = n;
	list <int> L;
	while(0 != temp)
	{
		L.push_front(temp % 2);
		temp = temp >> 1;
	}
 
	for(list <int>::iterator iter = L.begin(); iter != L.end(); iter++)
	{
		cout<<*iter;
	}
	cout <<endl;
}
 
//General method, 32 bit, step by step and 1 run and run
void Binarycout(int n)
{
	for(int i = 31; i>= 0; i--)
	{
		cout<<((n>>i)&1);
	}
 
	cout<<endl;
}
 
//Binary conversion using bitset
void BinaryBitset(int n)  //Use this function to include a bitset header file
{
	cout<<bitset<sizeof(int)*8>(n)<<endl;
}
 
int main()
{
	int a = 1045, b = 2;
	int c;
	c = a + b;
	cout<<setw(20)<<"BinaryRecursion("<<c<<"):";
	BinaryRecursion(c);
	cout<<endl;
 
	cout<<setw(20)<<"BinaryVector("<<c<<"):";
	BinaryVector(c);
 
	cout<<setw(20)<<"Binarycout("<<c<<"):";
	Binarycout(c);
 
	cout<<setw(20)<<"BinaryBitset("<<c<<"):";
	BinaryBitset(c);
 
	return (0);
}

Debug Run

Think and Tip

//Recursive Output Binary Function
void BinaryRecursion(int n)
{
	int a;
	a = n % 2; // Remaining
	n = n >> 1;  //To move one bit to the right is equivalent to dividing by two
	if(0 != n)
	{
		BinaryRecursion(n);
	}
	cout<<a;
}

Recursive Level

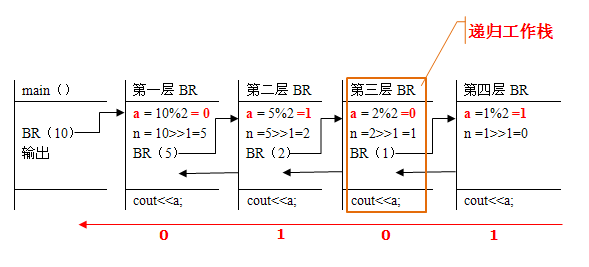
The cost of using recursion is enormous: it consumes a lot of memory!!Recursive loops use stacks, which have very limited resources.Assuming that the main function calling the recursive function is Layer 0, the recursive function is called from the main function into Layer 1, and the recursive call from Layer I I itself into Layer i+1.Conversely, exit layer I recursion should return to layer i-1.

In order to ensure the correct execution of recursive functions, the system needs to set up a "recursive workstack" as the data store used during the operation of the entire recursive function.The information required for each level of recursion constitutes a "work record" that includes all arguments, all local variables, and the return address of the previous level.

As each level of recursion enters, a new record of work is generated and pushed to the top of the stack.Each time a work record pops up from the top of the stack after exiting a layer of recursion, the current execution layer's work record must be the work record at the top of the recursive stack, which is called the "active record", and the top pointer indicating the active record is called the "current environment pointer".

As shown in the figure above: When n is not equal to 0, save the "work record" of the current layer, and then recursively call into the next layer until n is equal to 0, which is the fourth layer, putting the a value of the current layer
1. Print it out, then exit Layer 4 recursion and return to Layer 4-1, Layer 3.Then print a value of 0 for this layer and return to printing the rest of the layers in turn.The result is
1010.

Specify data output width: Use the function setw() provided by C++ to specify the width of the output data item.Setw() brackets usually give a positive integer value that limits the output width of the item immediately following it.For example, setw(8) means that the output of the data item immediately following it takes up eight characters wide.Setw() can only limit one data item immediately following it, and returns to the default output mode after output.Setw() must be used program Add another sentence at the beginning: #include<iomanip>

Reload link: C++ Binary, Decimal, Octal, and Hexadecimal Conversions