Description
Given the coordinates of N points in the plane, find the K far point pair under Euclidean distance.

Input
The first behavior of the input file is two integers N, K separated by spaces. Next N lines, two integers X,Y for each line, represent a point.
Coordinates. 1 < = N < = 100000, 1 < = K < = 100, K < = N * (N_1)/2, 0 < = X, Y < 2 ^ 31.

Output
The first action of the output file is an integer, representing the square of the distance of the K far point pair (which must be an integer).

Sample Input
10 5
0 0
0 1
1 0
1 1
2 0
2 1
1 2
0 2
3 0
3 1

Sample Output
9

Analysis:
kdtree
Because each point counts twice for us ((x, y) & (y, x))
So we should avoid the cumbersome judgment.
Let's just k*=2

One thing to note is the calculation of dis.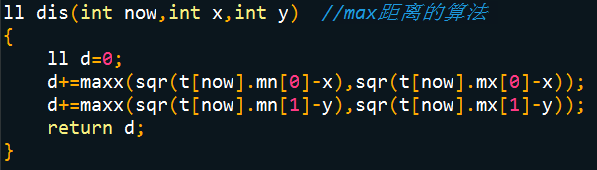

After doing several questions, we found that when calculating the nearest and farthest points,
dis is written differently

tip

At first I couldn't even pass the example.
The problem is in this sentence!!!

What is the reason for this?

Because we're looking for the point pair farthest from k, we're inserting it.
It must take out the smallest element in a queue and compare it with the current value.

Later, the mad WA went on and on.
After an hour of scrutiny, I found that a function should return ll, but I did not force type conversion.

Write code slices here.
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#define ll long long

using namespace std;

const int N=100010;
struct node{
    int l,r,d[2],mn[2],mx[2];
};
node t[N];
int n,k,root,cmpd,x,y;
priority_queue<ll,vector<ll>,greater<ll> >q;   ////

int cmp(const node &a,const node &b)
{
    return ((a.d[cmpd]<b.d[cmpd])||((a.d[cmpd]==b.d[cmpd])&&(a.d[!cmpd]<b.d[!cmpd])));
}

ll maxx(ll x,ll y) {if (x>y) return x;else return y;}
ll sqr(int x){return (ll)x*x;}

void update(int bh)
{
    int lc=t[bh].l;
    int rc=t[bh].r;
    if (lc)
    {
        t[bh].mn[0]=min(t[bh].mn[0],t[lc].mn[0]);
        t[bh].mn[1]=min(t[bh].mn[1],t[lc].mn[1]);
        t[bh].mx[0]=max(t[bh].mx[0],t[lc].mx[0]);
        t[bh].mx[1]=max(t[bh].mx[1],t[lc].mx[1]);
    }
    if (rc)
    {
        t[bh].mn[0]=min(t[bh].mn[0],t[rc].mn[0]);
        t[bh].mn[1]=min(t[bh].mn[1],t[rc].mn[1]);
        t[bh].mx[0]=max(t[bh].mx[0],t[rc].mx[0]);
        t[bh].mx[1]=max(t[bh].mx[1],t[rc].mx[1]);
    }
}

int build(int l,int r,int D)
{
    cmpd=D;
    int mid=(l+r)>>1;
    nth_element(t+l+1,t+mid+1,t+1+r,cmp);   ////////// 
    t[mid].mn[0]=t[mid].mx[0]=t[mid].d[0];
    t[mid].mn[1]=t[mid].mx[1]=t[mid].d[1];
    if (l!=mid) t[mid].l=build(l,mid-1,!D);
    if (r!=mid) t[mid].r=build(mid+1,r,!D);
    update(mid);
    return mid;
}

ll dis(int now,int x,int y)  //Algorithm of max distance 
{
    ll d=0;
    d+=maxx(sqr(t[now].mn[0]-x),sqr(t[now].mx[0]-x));
    d+=maxx(sqr(t[now].mn[1]-y),sqr(t[now].mx[1]-y));
    return d;
}

void ask(int now)
{
    ll d0,dl,dr;
    d0=sqr(x-t[now].d[0])+sqr(y-t[now].d[1]);
    if (t[now].l) dl=dis(t[now].l,x,y);
    else dl=0;
    if (t[now].r) dr=dis(t[now].r,x,y);
    else dr=0;
    if (d0>q.top()) q.pop(),q.push(d0);
    if (dl>dr)   //The longest distance 
    {
        if (dl>q.top()) ask(t[now].l);
        if (dr>q.top()) ask(t[now].r);
    }
    else
    {
        if (dr>q.top()) ask(t[now].r);
        if (dl>q.top()) ask(t[now].l);
    }
}

int main()
{
    scanf("%d%d",&n,&k); k*=2;
    for (int i=1;i<=k;i++) q.push(0);   ////////
    for (int i=1;i<=n;i++)
        scanf("%d%d",&t[i].d[0],&t[i].d[1]);
    root=build(1,n,0);
    for (int i=1;i<=n;i++)
    {
        x=t[i].d[0]; y=t[i].d[1];
        ask(root);
    }
    printf("%lld",q.top());
    return 0;
}