Description

Give N,M,K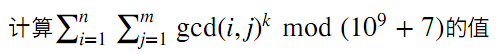

Input

There are multiple groups of data in the input. The first row of the input data contains two positive integers T and K, which represent the group of T data. The meaning of K is as shown above. The second row below goes to the row T+1. Each row contains two positive integers n and m, whose meaning is as shown above.
Output

For example
Sample Input

1 2

3 3
Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

Explanation:
Orz YZH

JudgeOnline/upload/201603/4407.rar

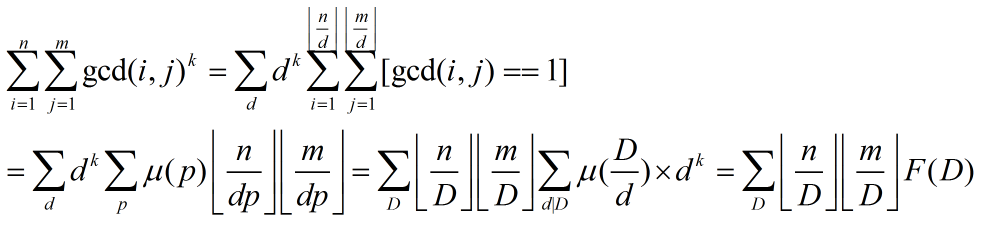
It's the first time to do Dirichlet convolution. The convolution F (D) of two product functions is product function, which can be obtained by linear sieve.
If D is prime, F(D)=D^k-1
If D is not a prime number, it will be screened by its smallest quality factor p to f (d) = f (D / P) × p ^ k

Code

#include<bits/stdc++.h>
#define ll long long
#define inf 1000000000
#define mod 1000000007
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int N=5000001;
int F[N],f[N],flag[N],k,tot,p[N],ans;
inline int gpow(int x,int y)
{
    int ans=1;
    while (y)
    {
        if (y&1) ans=(ll)ans*x%mod;
        y>>=1;x=(ll)x*x%mod;
    }
    return ans;
}
void preparation()
{
    F[1]=1;
    for (int i=2;i<N;i++)
    {
        if (!flag[i]){f[i]=gpow(i,k);F[i]=f[i]-1;p[++tot]=i;}
        for (int j=1;j<=tot&&i*p[j]<N;j++)
        {
            flag[i*p[j]]=1;
            if (i%p[j])F[i*p[j]]=(ll)F[i]*F[p[j]]%mod;
            else{F[i*p[j]]=(ll)F[i]*f[p[j]]%mod;break;}
        }
    }
    for (int i=1;i<N;i++) (F[i]+=F[i-1])%=mod;
}
int main()
{
    int Case=read();k=read();
    preparation();
    while (Case--)
    {
        int n=read(),m=read();if (n>m) swap(n,m);ans=0;
        for (int i=1,pos=0;i<=n;i=pos+1)
        {
            pos=min(n/(n/i),m/(m/i));
            (ans+=1LL*(n/i)*(m/i)%mod*(F[pos]-F[i-1])%mod)%=mod;
        }
        printf("%d\n",(ans+mod)%mod);
    }
    return 0;
}