Face
Topic: Give you a tree, XJB pick a spot to divide and ask for the desired complexity.

According to my crude understanding of expectation, expectation is an integral, so it satisfies linear operations such as integral addition and subtraction.So here you can consider the expected complexity for each point.

For point x, the expected depth of X in the point tree is what it expects.

Using the linear property of the expectation again, we can find the probability of x in the y-subtree for each y, from which we can deduce the expectation.

After a small analysis, it is found that x is in the subtree of y, and that if y is first selected to divide on the path of x-y, the probability is 1 dis (x, y), which is what y expects for X.

Then the answer to the original question is

If dis(i,j) is not in the denominator, it is the point division of a fruit.

Let's change the order of enumeration, and set f[x] to the logarithm of the points at a distance of x, and change it to nx=1f[x], and we'll get the answer.

Also consider point division, find the center of gravity x, and consider the path of X.
For each connected block.Find the distance from each of their points to x, and set g[i] as the number of points from X to I.We find that the contribution of two g's to the answer is a convolution and can be optimized by fft.

Complexity O(nlog2n) is expected, but in theory, without optimization, it would be a chrysanthemum card.
Like this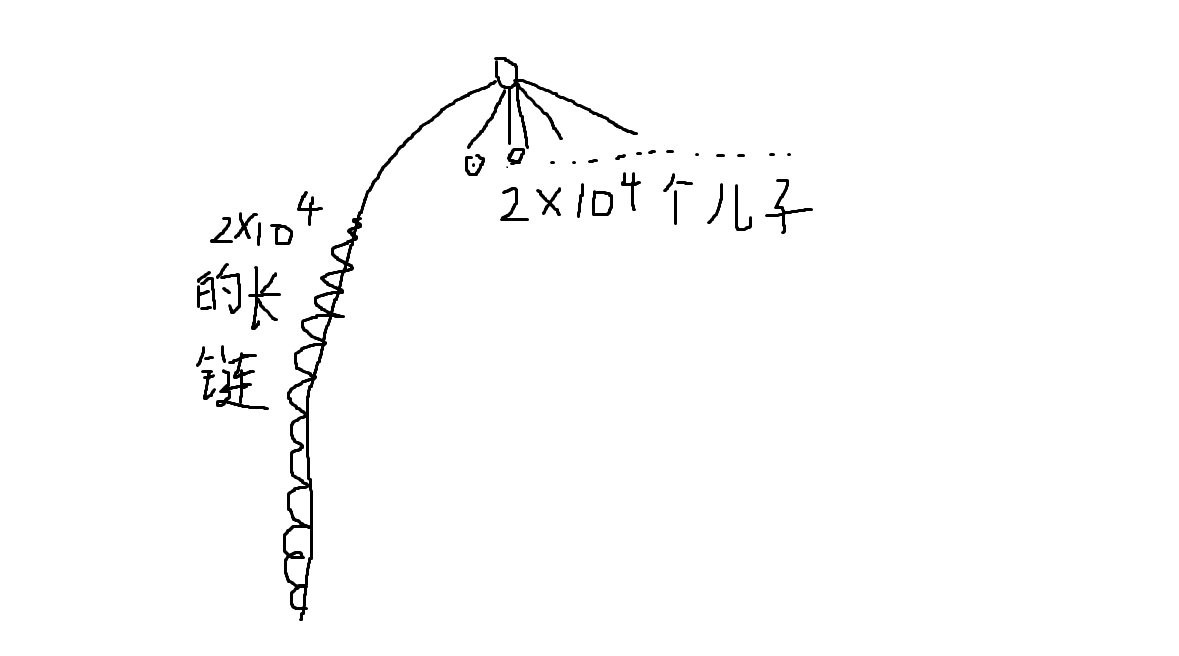

The number bound of FFTs is extended by a long chain, and then FFTs are made continuously with a large number of times bounds.
Connection blocks with small depths should be made before those with large depths.

#include <iostream>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;
#define mmst(a, b) memset(a, b, sizeof(a))
#define mmcp(a, b) memcpy(a, b, sizeof(b))

typedef long long LL;

const int N=60060,oo=1e9+7;
const LL g=3,p=1004535809;

int n,rev[N];
int nn;
int to[N],nex[N],head[N],cnt;
int root,sum,siz[N],d[N],dep[N],len,slen;
LL a[N],b[N],c[N],ans[N];
double res=0.0;
bool vis[N];

void read(int &hy)
{
    hy=0;
    char cc=getchar();
    while(cc<'0'||cc>'9')
    cc=getchar();
    while(cc>='0'&&cc<='9')
    {
        hy=(hy<<3)+(hy<<1)+cc-'0';
        cc=getchar();
    }
}

LL cheng(LL a,LL b)
{
    LL res=1ll;
    for(;b;b>>=1,a=a*a%p)
    if(b&1)
    res=res*a%p;
    return res;
}

void init(int lim)
{
    int k=-1;
    n=1;
    while(n<lim)
    n<<=1,k++;
    for(int i=0;i<n;i++)
    rev[i]=(rev[i>>1] >> 1) | ((i&1)<<k);
}

void ntt(LL *a,int ops)
{
    for(int i=0;i<n;i++)
    if(i<rev[i])
    swap(a[i],a[rev[i]]);
    for(int l=2;l<=n;l<<=1)
    {
        int m=l>>1;
        LL wn;
        if(ops)
        wn=cheng(g,(p-1)/l);
        else
        wn=cheng(g,p-1-(p-1)/l);
        for(int i=0;i<n;i+=l)
        {
            LL w=1ll;
            for(int k=0;k<m;k++)
            {
                LL t=a[i+k+m]*w%p;
                a[i+k+m]=(a[i+k]-t+p)%p;
                a[i+k]=(a[i+k]+t)%p;
                w=w*wn%p;
            }
        }
    }
    if(!ops)
    {
        LL Inv=cheng(n,p-2);
        for(int i=0;i<n;i++)
        a[i]=a[i]*Inv%p;
    }
}

void add(int u,int v)
{
    to[++cnt]=v;
    nex[cnt]=head[u];
    head[u]=cnt;
}

void dfsRoot(int x,int fa)
{
    d[x]=0;
    siz[x]=1;
    for(int h=head[x];h;h=nex[h])
    if(!vis[to[h]]&&to[h]!=fa)
    {
        dfsRoot(to[h],x);
        siz[x]+=siz[to[h]];
        d[x]=max(d[x],siz[to[h]]);
    }
    d[x]=max(d[x],sum-siz[x]);
    if(d[x]<d[root])
    root=x;
}

void dfsLen(int x,int fa)
{
    len=max(len,dep[x]);
    a[dep[x]]++;
    for(int h=head[x];h;h=nex[h])
    if(!vis[to[h]]&&to[h]!=fa)
    {
        dep[to[h]]=dep[x]+1;    
        dfsLen(to[h],x);
    }
}

void dfsSol(int x)
{
    vis[x]=1;
    slen=1;
    b[0]=1;
    for(int h=head[x];h;h=nex[h])
    if(!vis[to[h]])
    {
        len=0;
        dep[to[h]]=1;
        dfsLen(to[h],0);

        init(len+slen+1);
        for(int i=0;i<n;i++)
        c[i]=b[i];

        for(int i=0;i<=len;i++)
        b[i]+=a[i];

        ntt(c,1);
        ntt(a,1);

        for(int i=0;i<n;i++)
        c[i]=c[i]*a[i]%p;

        ntt(c,0);
        for(int i=0;i<n;i++)
        ans[i]+=c[i];

        for(int i=0;i<n;i++)
        a[i]=0;
        slen=max(slen,len);
    }
    for(int i=0;i<=slen;i++)
    b[i]=0;
    for(int h=head[x];h;h=nex[h])
    if(!vis[to[h]])
    {
        root=0;
        sum=siz[to[h]];
        dfsRoot(to[h],0);
        dfsSol(root);
    }
}

int main()
{
    cin>>nn;

    for(int i=1;i<nn;i++)
    {
        int u,v;
        read(u);
        read(v);
        u++;
        v++;
        add(u,v);
        add(v,u);
    }
    sum=nn;
    root=0;
    d[0]=oo;
    dfsRoot(1,0);
    dfsSol(root);

    for(int i=1;i<nn;i++)
    res+=2.0*ans[i]/(i+1);
    res+=nn;
    printf("%.4lf\n",res);
}