BZOJ 3224
meaning of the title
There are n operations, a total of 6.
| number | operation | Meaning |
|---|---|---|
| 1 | insert(x) | Insert a number x |
| 2 | remove(x) | Delete a number x, delete more than one |
| 3 | rank(x) | Find out the ranking of x, multiple minimum |
| 4 | kth(x) | Find the number of decimal k |
| 5 | pred(x) | The largest number less than x |
| 6 | succ(x) | The smallest number greater than x |
sample input
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
sample output
106465
84185
492737
SOL
This problem actually covers the basic operation of SBT (Size Balanced Tree balanced binary tree). Here are some explanations.
Note: My method is to set up a node for each number. I can also put the same number on one node, but it's a bit complicated to write and put it at the end.
Definition
Definition of SBT: A node, any child is no less than the other children's children.
Simply put, any node is older than its brother's children.
Figure: L is larger than C and D, R is larger than A and B. 
Define the structure tree, where key is the node value, left and right are the left and right child numbers, and size is the subtree size.
struct SBT
{
int key,left,right,size;
} tree[N]; rotate
In fact, rotation is the most basic operation of SBT, which is why SBT can maintain its balance.
As shown in the figure, basically look at the code to understand, do not omit the operation. 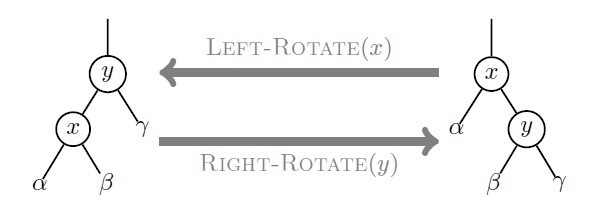
void left_rotate(int &x)
{
int y = tree[x].right;
tree[x].right = tree[y].left;
tree[y].left = x;
tree[y].size = tree[x].size;
tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
x = y;
}
void right_rotate(int &x)
{
int y = tree[x].left;
tree[x].left = tree[y].right;
tree[y].right = x;
tree[y].size = tree[x].size;
tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
x = y;
} Maintain
Another basic operation of SBT is maintenance.
Yeah, I haven't talked about how to achieve this balance yet.

It can be divided into the following situations:
I. A is greater than R
1. Call right_rotate(T);

2. R has not changed, L and T have changed, so call maintain(T) and maintain(T).
2. B is greater than R

1. Call left_rotate(L);

2. Call right_rotate(T);

3. R does not change at this time, so maintain(L), maintain(T), maintain(B) are called.
Tip!
Pay attention to calling maintain tain from bottom to top! Otherwise, the rotation above will affect the nodes below.
The same is true for the other two cases.
void maintain(int &x,bool flag)
{
if (flag == false)
{
if (tree[tree[tree[x].left].left].size > tree[tree[x].right].size)//The left child's left subtree is larger than the right child's.
right_rotate(x);
else if (tree[tree[tree[x].left].right].size > tree[tree[x].right].size)//The right subtree of the right child is larger than that of the right child.
{
left_rotate(tree[x].left);
right_rotate(x);
}
else return;
}
else
{
if(tree[tree[tree[x].right].right].size > tree[tree[x].left].size)//The right subtree of the right child is larger than that of the left child.
left_rotate(x);
else if(tree[tree[tree[x].right].left].size > tree[tree[x].left].size)//The left subtree of the right child is larger than that of the left child.
{
right_rotate(tree[x].right);
left_rotate(x);
}
else return;
}
maintain(tree[x].left,false);
maintain(tree[x].right,true);
maintain(x,true);
maintain(x,false);
}insert
Finally get to the point!
Insertion operation is relatively simple, as long as it is maintain ed after insertion.
void insert(int &x,int key)
{
if(x == 0)
{
x = ++tot;
tree[x].left = tree[x].right = 0;
tree[x].size = 1;
tree[x].key = key;
}
else
{
tree[x].size ++;
if(key < tree[x].key) insert(tree[x].left,key);
else insert(tree[x].right,key);
maintain(x,key>=tree[x].key);
}
}delete
Deleting is a bit troublesome. My method here is that if there is no subtree, it is the best; if there is only left subtree or right subtree, then hang the subtree; if there are two subtrees, then find the successor node instead of the current location. Actually, we need to call maintain tain for reasoning, but it doesn't really matter.
void remove(int &x,int key)
{
tree[x].size --;
if (key > tree[x].key)
remove(tree[x].right,key);
else if(key < tree[x].key)
remove(tree[x].left,key);
else
{
if(tree[x].left != 0 && tree[x].right == 0) x = tree[x].left;//Only left subtree
else if(tree[x].left ==0 && tree[x].right != 0) x = tree[x].right;//Only right subtree
else if(tree[x].left ==0 && tree[x].right == 0) x = 0;//No left subtree and right subtree
else //Find the smallest element in the right subtree
{
int temp = tree[x].right;
while(tree[temp].left) temp = tree[temp].left;
tree[x].key = tree[temp].key;
remove(tree[x].right,tree[temp].key);
}
}
}Ranking
Continuous search on the binary tree. Here's the only trouble with duplicating nodes: because nodes may duplicate, and left subtrees may have the same nodes, so don't stop immediately, but record the current answer and continue to search to the left.
void GetRank(int &x,int key,int sum)//Find the number of key s
{
if (x == 0) return;
if (key == tree[x].key)
{
res = min(res,sum+tree[tree[x].left].size+1);
GetRank(tree[x].left,key,sum);
}
if(key < tree[x].key) GetRank(tree[x].left,key,sum);
if(key > tree[x].key) GetRank(tree[x].right,key,sum+tree[tree[x].left].size+1);
} Find the k smallest value
It is quite convenient to find the smallest value of K by repeating open nodes, and the size of left subtree is exactly equal to k-1.
int GetKth(int &x,int k)//Find the k decimal
{
int r = tree[tree[x].left].size + 1;
if(r == k) return tree[x].key;
else if(r < k) return GetKth(tree[x].right,k - r);
else return GetKth(tree[x].left,k);
} Forerunners and successors
int pred(int &x,int y,int key)
{
if(x == 0) return y;
if(key > tree[x].key)
return pred(tree[x].right,x,key);
else return pred(tree[x].left,y,key);
}
int succ(int &x,int y,int key)
{
if(x == 0) return y;
if(key < tree[x].key)
return succ(tree[x].left,x,key);
else return succ(tree[x].right,y,key);
}