101. Symmetric binary tree
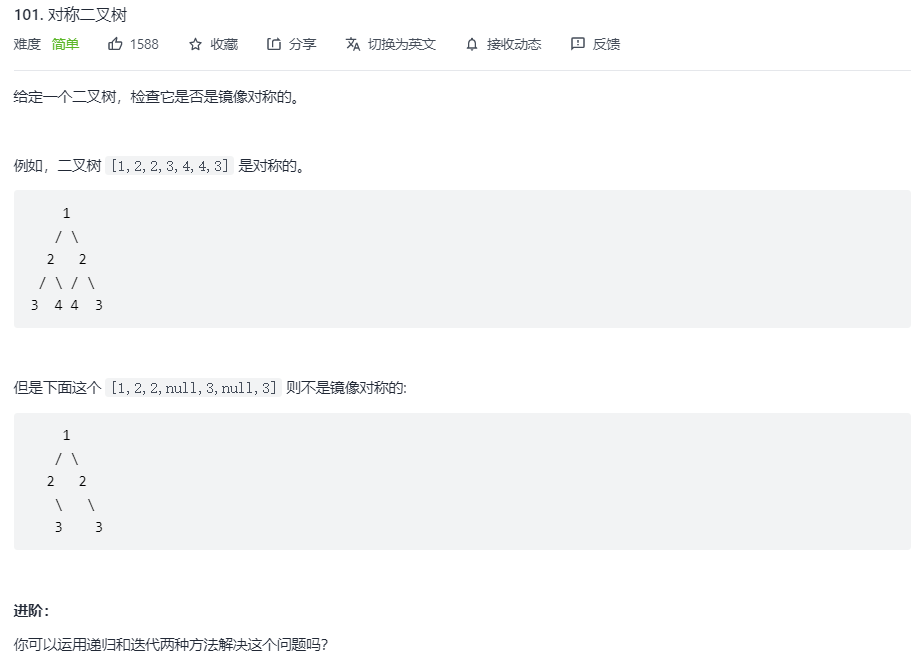
To judge whether the mirror image is symmetrical, make a dotted line in the middle to judge whether the half fold coincides. For example, the root node depends on whether its left child node and right child node are the same, and then the left child node of the left child node and the right child node of the right child node...
1. Recursion
public boolean isSymmetric(TreeNode root) {
return isMirror(root,root);
}
private boolean isMirror(TreeNode left,TreeNode right){
//true if both are empty at this time
if(left==null&&right==null)return true;
//false if only one is null or the values are unequal
if((left==null||right==null)||(right.val!=left.val))return false;
//Recursively view the following nodes
return isMirror(left.right,right.left)&&isMirror(left.left,right.right);
}
2. Iteration
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
Deque<TreeNode> queue=new LinkedList<>();
queue.add(root.left);
queue.add(root.right);
while(!queue.isEmpty()){
TreeNode left=queue.poll();
TreeNode right=queue.poll();
if(left==null&&right==null)continue;
if(left==null||right==null||left.val!=right.val) return false;
queue.add(left.left);
queue.add(right.right);
queue.add(left.right);
queue.add(right.left);
}
return true;
}
104. Maximum depth of binary tree

The depth of the binary tree is the maximum value from the root node to the leaf nodes of the left and right subtrees. If this layer is not empty, its depth is + 1. So we find the depth of the left and right subtrees, and then take the maximum, plus the depth of our own layer (that is, 1).
1. Recursion
public int maxDepth(TreeNode root) {
if(root==null) return 0;
int left=maxDepth(root.left);
int right=maxDepth(root.right);
return Math.max(left,right)+1;
}
2. Iteration
public int maxDepth(TreeNode root) {
Deque<TreeNode> queue=new LinkedList<>();
int res=0;
if(root==null) return 0;
queue.add(root);
while(!queue.isEmpty()){
res++;
for(int i=queue.size();i>0;i--){
TreeNode node=queue.poll();
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
}
return res;
}
However, the problem of iterative efficiency is relatively low, and the interview needs to be able to.
105. Construct binary tree from preorder and inorder traversal sequences

Just handle the boundary. The drawing is very clear and can be seen
Map<Integer,Integer> map=new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return dfs(preorder,inorder,0,preorder.length-1,0,preorder.length-1);
}
private TreeNode dfs(int[] preorder, int[] inorder,int pl,int pr,int il,int ir){
if(pl>pr||il>ir)return null;
int root=preorder[pl];
//Get the location of root
int index=map.get(root);
//The left subtree of root has k nodes
int k=index-il;
TreeNode node=new TreeNode(root);
node.left=dfs(preorder,inorder,pl+1,pl+k,il,index-1);
node.right=dfs(preorder,inorder,pl+k+1,pr,index+1,ir);
return node;
}
106. Construct binary tree from middle order and post order traversal sequences
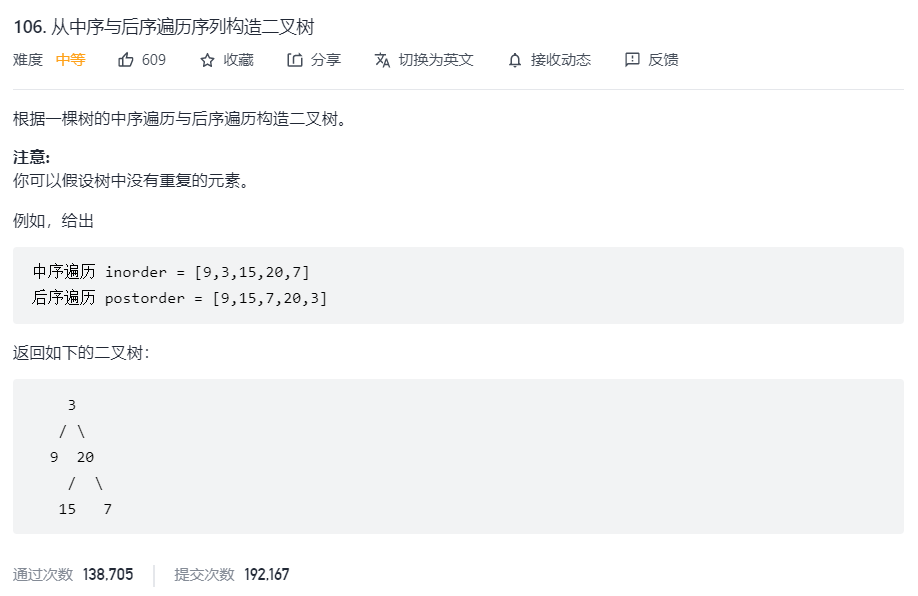

If you can understand the above figure, you can use the above figure. If you can't understand it, you can read my notes below. The same is true
Map<Integer,Integer> map=new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return dfs(postorder,inorder,0,postorder.length-1,0,postorder.length-1);
}
private TreeNode dfs(int[] postorder,int[] inorder,int pl,int pr,int il,int ir){
if(pl>pr||il>ir)return null;
int root=postorder[pr];
//Get the location of root
int index=map.get(root);
//The left subtree of root has k elements
int k=index-il;
TreeNode node=new TreeNode(root);
node.left=dfs(postorder,inorder,pl,pl+k-1,il,index-1);
node.right=dfs(postorder,inorder,pl+k,pr-1,index+1,ir);
return node;
}
112. Path sum
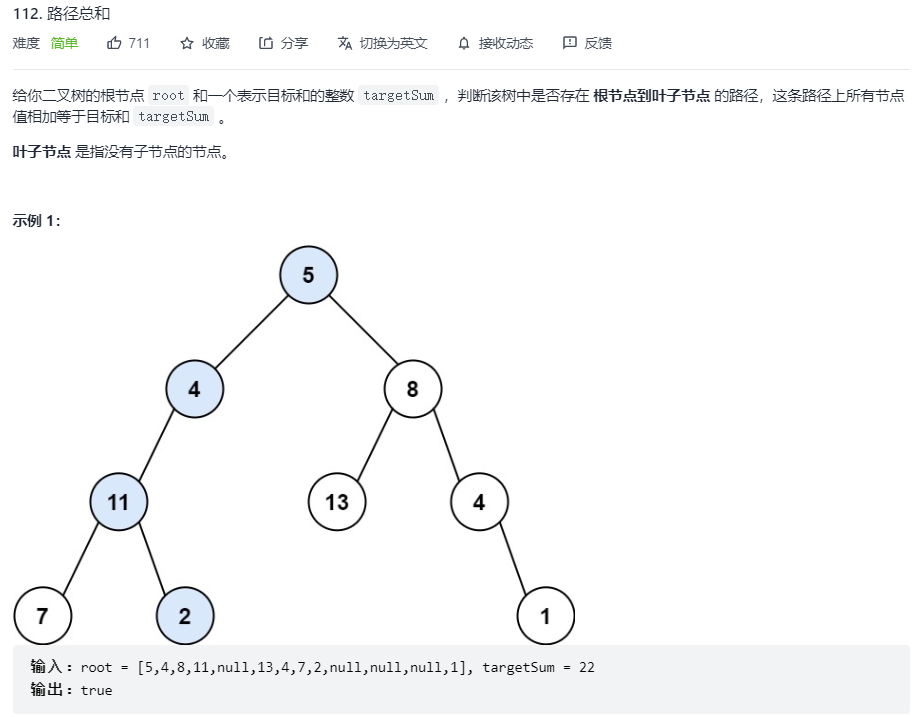
Recursive left and right subtree
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null) return false;
if(root.left==null&&root.right==null) return root.val==targetSum;
boolean left=hasPathSum(root.left,targetSum-root.val);
boolean right=hasPathSum(root.right,targetSum-root.val);
return left||right;
}
116. Populate the next right node pointer for each node
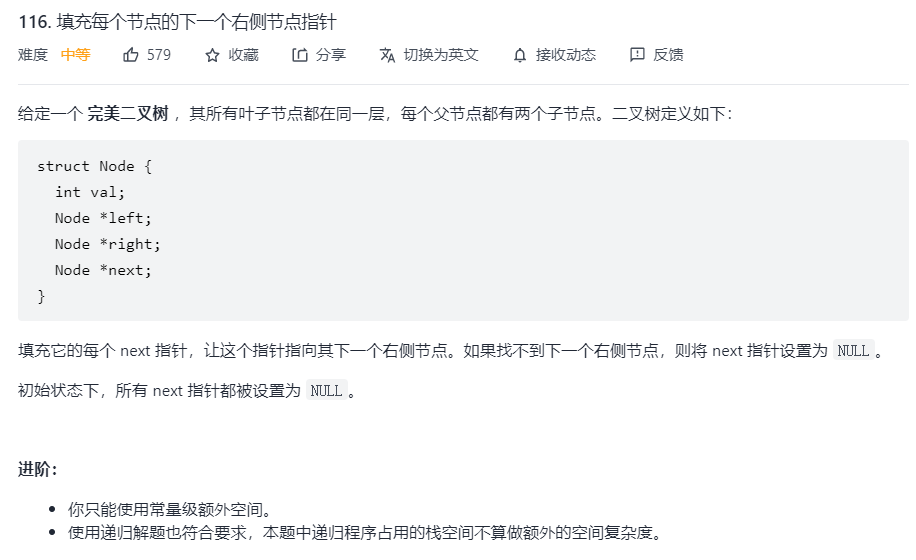

It's easy to think of iterative solution
public Node connect(Node root) {
if(root==null) return null;
Deque<Node> queue=new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
Node pre=queue.poll();
int size=queue.size();
if(pre.left!=null)queue.add(pre.left);
if(pre.right!=null)queue.add(pre.right);
for(int i=0;i<size;i++){
Node cur=queue.poll();
pre.next=cur;
if(cur.left!=null)queue.add(cur.left);
if(cur.right!=null)queue.add(cur.right);
pre=cur;
}
pre.next=null;
}
return root;
}
However, this space complexity does not meet the requirements. Optimize it and do not use queue storage
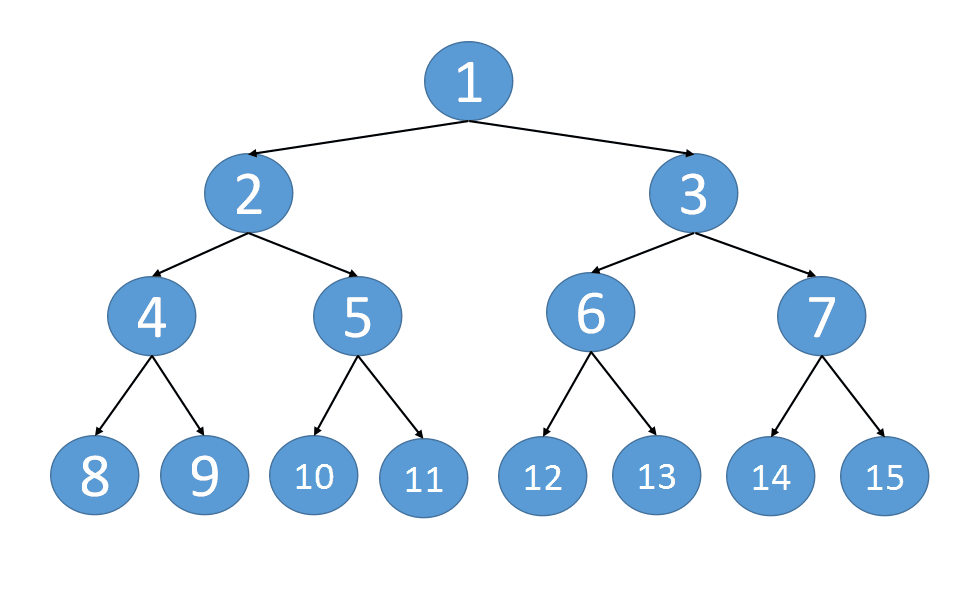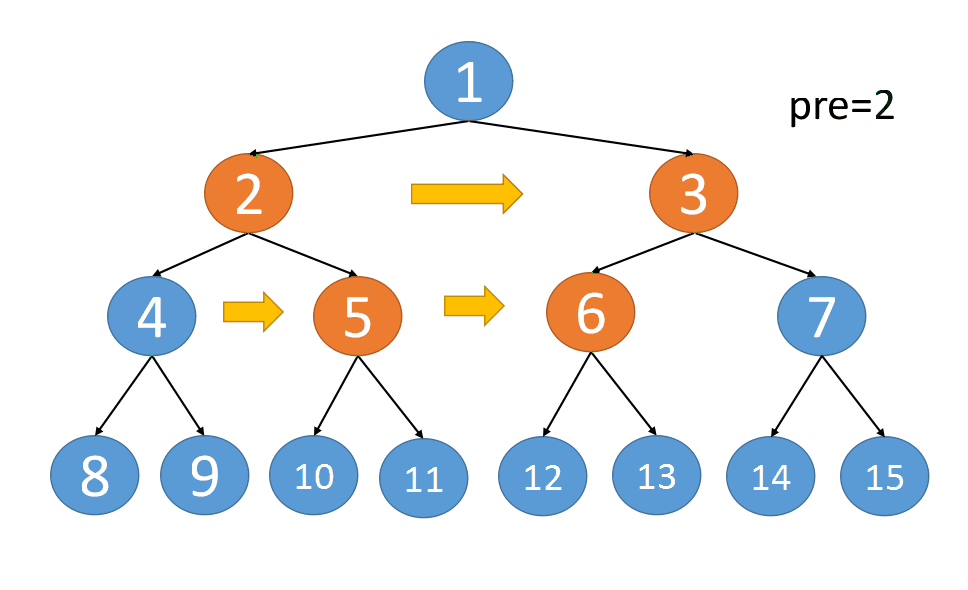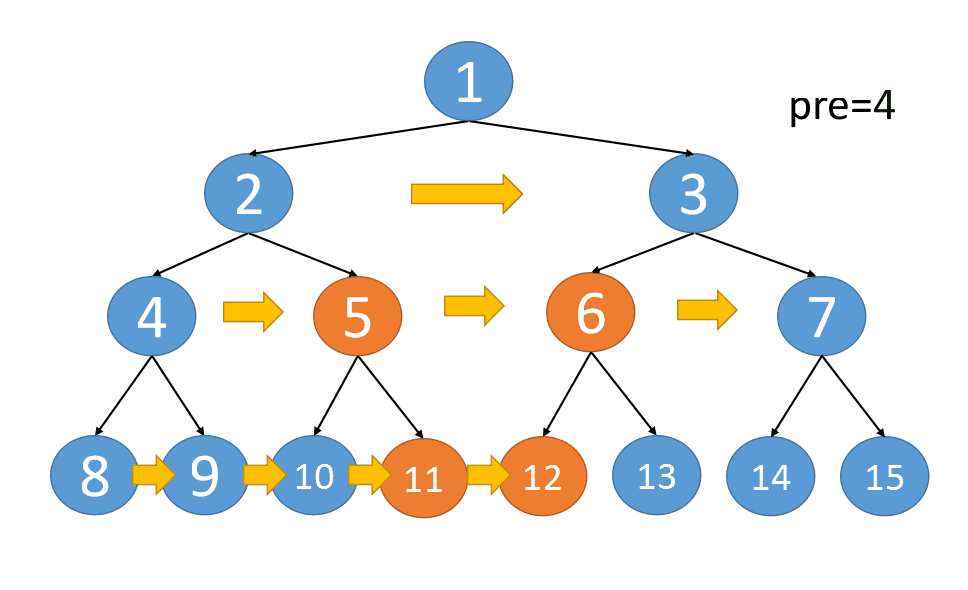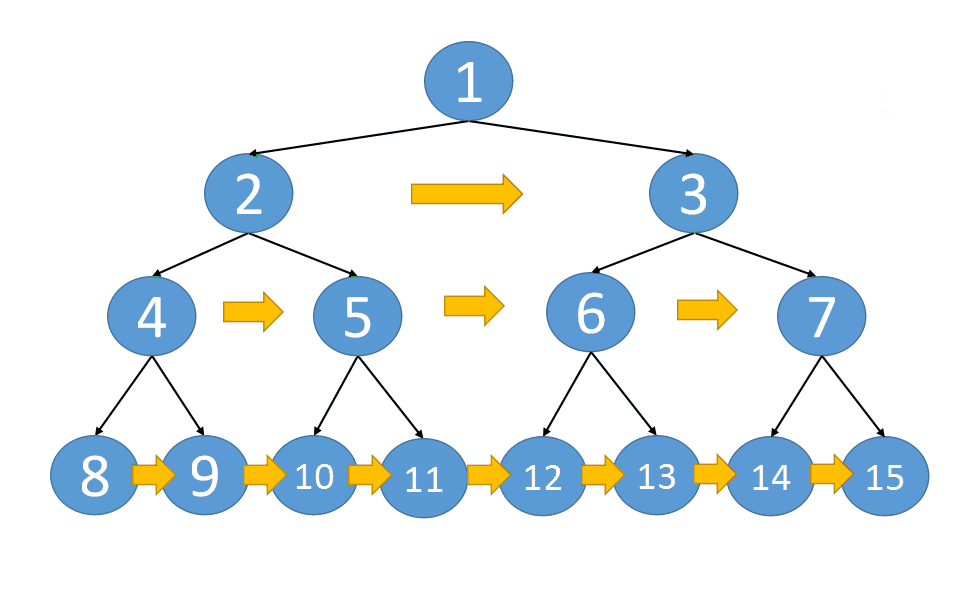
class Solution {
public Node connect(Node root) {
if(root==null) return null;
Node pre = root;
while(pre.left!=null) {
Node tmp = pre;
while(tmp!=null) {
tmp.left.next = tmp.right;
if(tmp.next!=null) {
tmp.right.next = tmp.next.left;
}
tmp = tmp.next;
}
pre = pre.left;
}
return root;
}
}
recursion
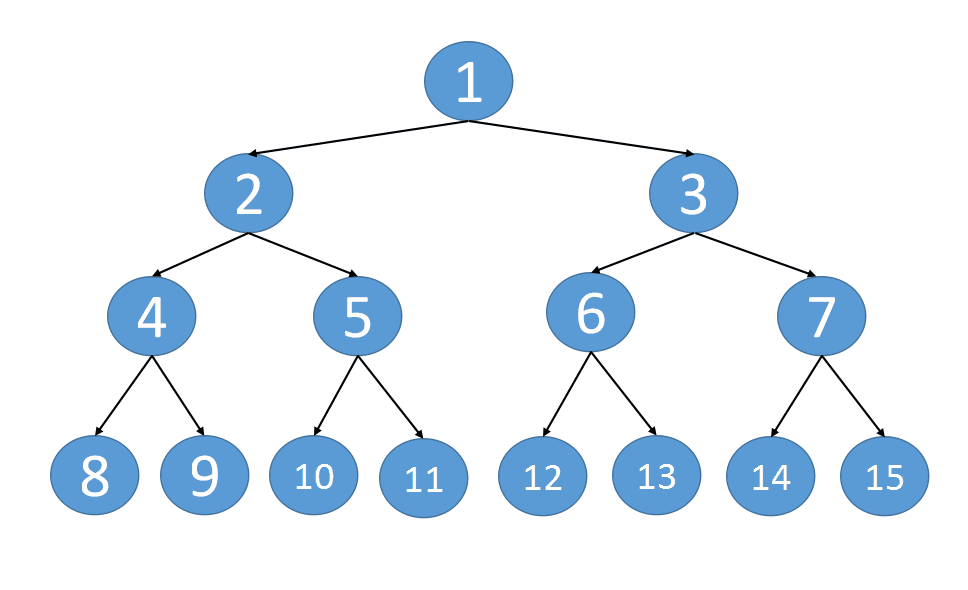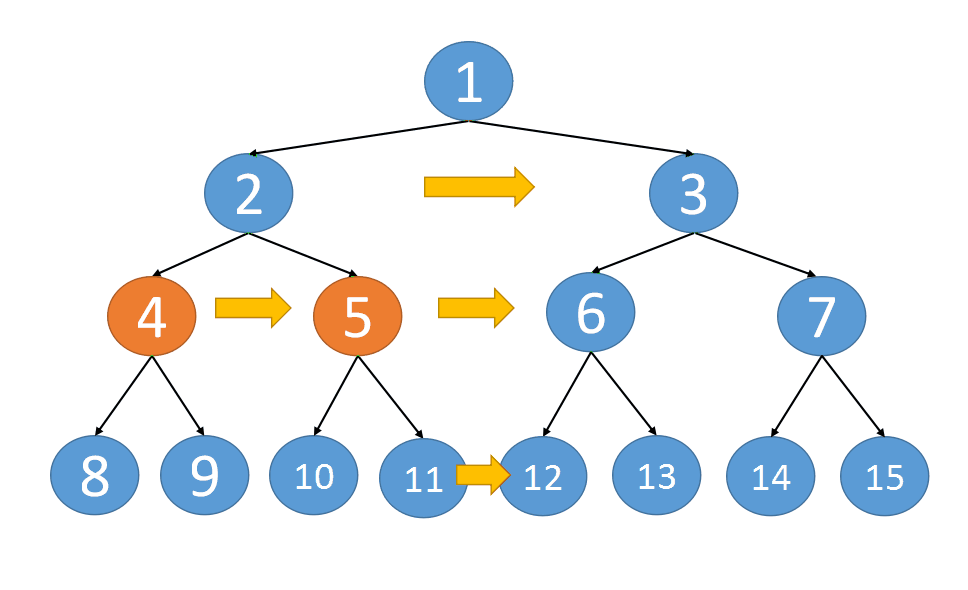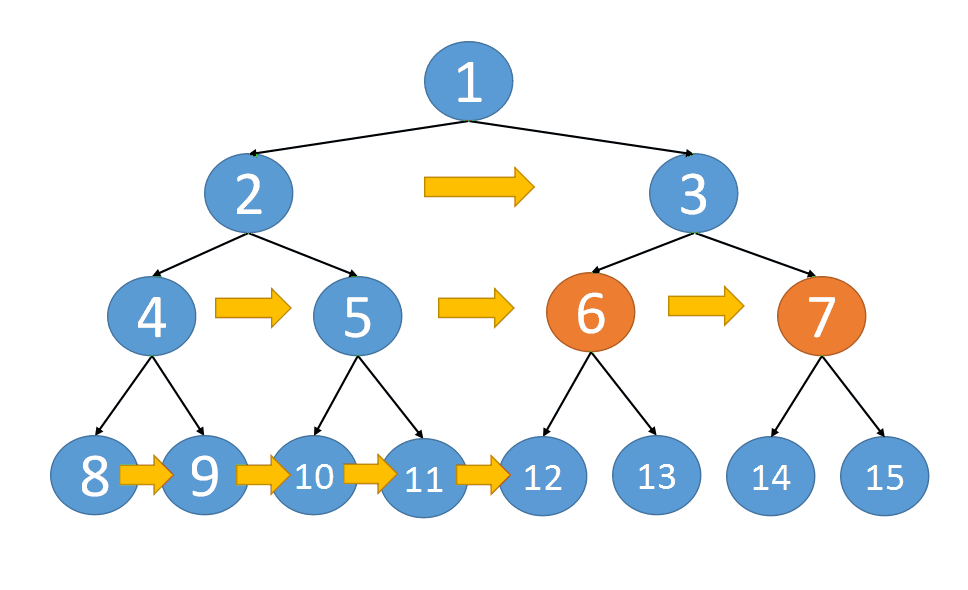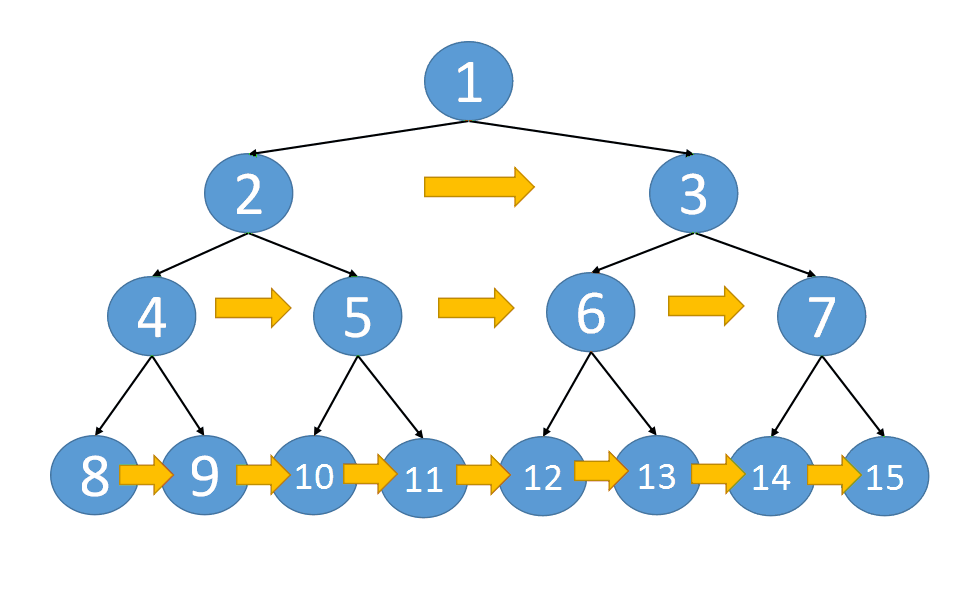
class Solution {
public Node connect(Node root) {
dfs(root);
return root;
}
private void dfs(Node root) {
if(root==null) {
return;
}
Node left = root.left;
Node right = root.right;
while(left!=null) {
left.next = right;
left = left.right;
right = right.left;
}
dfs(root.left);
dfs(root.right);
}
}
Reference from: Animation demonstration + three implementations
117. Fill in the next right node pointer II of each node

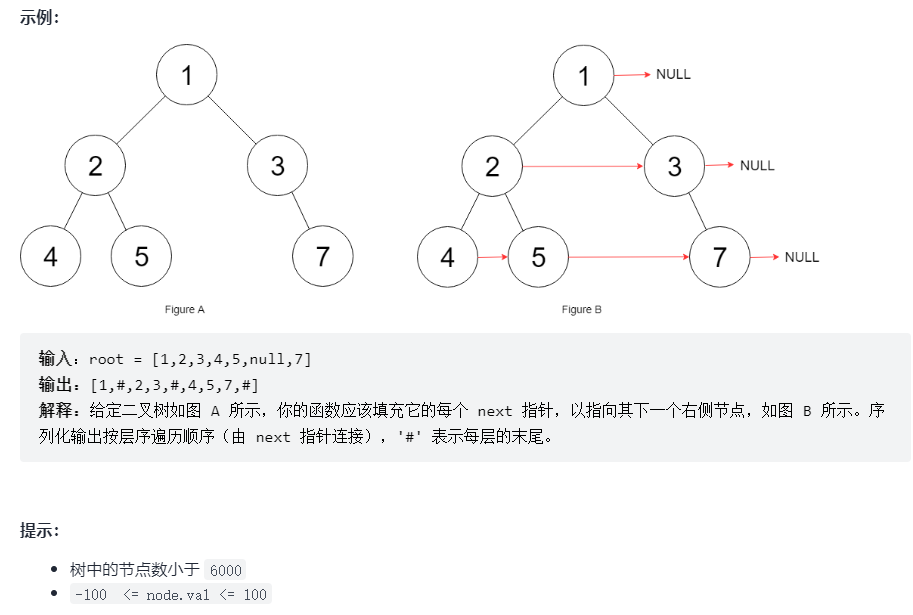
Iteration:
public Node connect(Node root) {
if(root==null)return null;
Node cur=root;
while(cur!=null){
Node dummy=new Node();
Node pre=dummy;
while(cur!=null){
//First connect your own subtree
if(cur.left!=null){
pre.next=cur.left;
pre=pre.next;
}
if(cur.right!=null){
pre.next=cur.right;
pre=pre.next;
}
//Then connect the on the right across the subtree
cur=cur.next;
}
//Next, start with the leftmost subtree (depending on the connection of the previous layer)
cur=dummy.next;
}
return root;
}
After reading the problem solution of recursion, I don't understand it. I think this is suitable for iteration. (I'm too good, woo woo)
199. Right view of binary tree
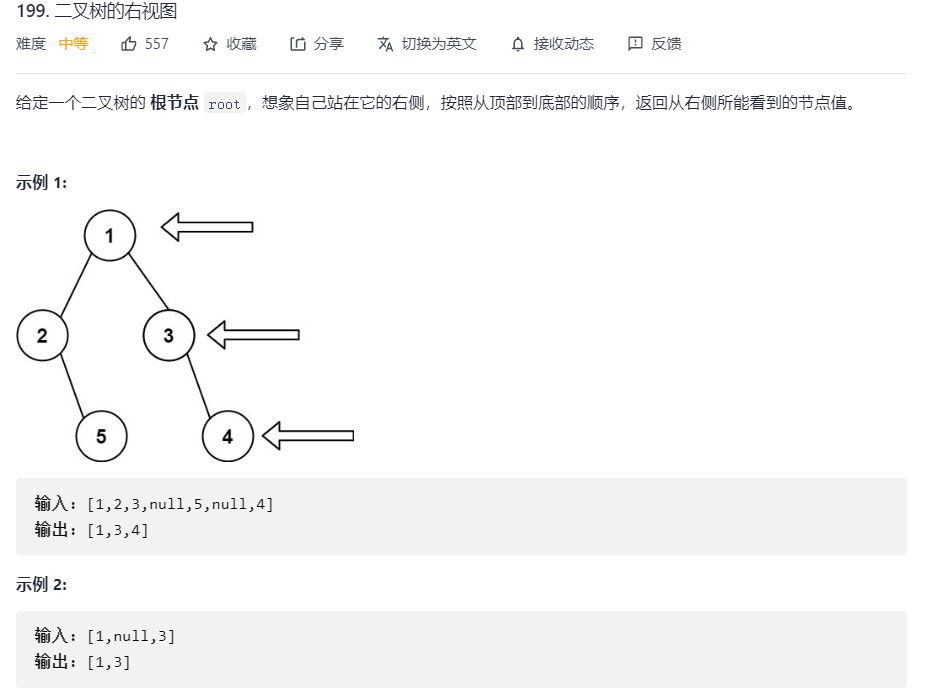
Level traversal, queue in turn, and take the last element of the queue each time
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res=new LinkedList<>();
if(root==null) return res;
Deque<TreeNode> q=new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
for(int i=q.size();i>0;i--){
TreeNode node=q.poll();
if(i==1){
res.add(node.val);
}
if(node.left!=null){
q.add(node.left);
}
if(node.right!=null){
q.add(node.right);
}
}
}
return res;
}
235. Nearest common ancestor of binary search tree

Because this problem is a binary search tree, we can make full use of its characteristics
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(p.val>root.val&&q.val>root.val){
return lowestCommonAncestor(root.right,p,q);
}
if(p.val<root.val&&q.val<root.val){
return lowestCommonAncestor(root.left,p,q);
}
return root;
}
236. Nearest common ancestor of binary tree

Recursively go to the left and right subtrees to find the positions of p and q, and then judge
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null||root==p||root==q)return root;
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left!=null&&right!=null)return root;
else if(left==null) return right;
return left;
}