http://blog.csdn.net/runatworld/article/details/50774215

BP Neural Network

Today, we talk about BP neural network. Neural network is based on BP neural network. machine learning It is widely used in many fields, such as function approximation, pattern recognition, classification, data compression and data processing.

Mining and other fields. Next, the principle and implementation of BP neural network are introduced.

 

Contents

 

1. Recognition of BP Neural Network

2. Selection of Implicit Layer

3. Forward Transfer Subprocesses

4. Reverse Transfer Subprocesses

5. Attentions of BP Neural Network

6. C++ Implementation of BP Neural Network

 

 

1. Recognition of BP Neural Network

 

Back Propagation neural network is divided into two processes

 

(1) Forward transmission sub-process of working signal

(2) Reverse transmission sub-process of error signal

 

In BP neural network, a single sample has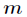There are three inputs.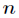There are usually several hidden layers between the input layer and the output layer. Actual

In 1989, Robert Hecht-Nielsen proved that a BP network with an implicit layer can be used for a continuous function in any closed interval.

This is the universal approximation theorem. So a three-layer BP network can accomplish arbitrary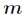Dimension to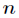Dimensional mapping. That's the three layers.

They are input layer (I), hidden layer (H), output layer (O). The following illustration

 

        

 

 

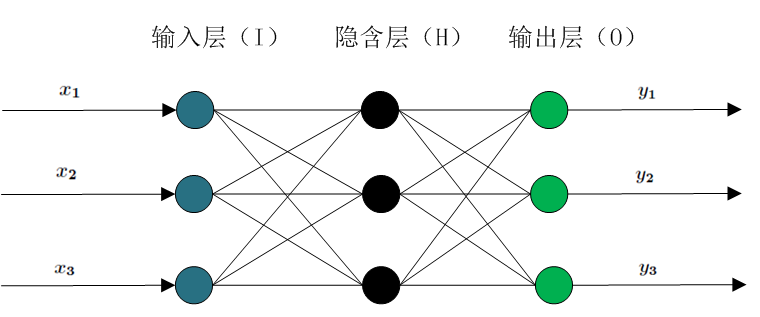
2. Selection of Implicit Layer

 

In BP neural network, the number of nodes in input layer and output layer is determined, while the number of nodes in hidden layer is uncertain, so how much should be set?

Is that right? In fact, the number of nodes in the hidden layer has an effect on the performance of the neural network. There is an empirical formula to determine the hidden layer.

The number of nodes is as follows

 

                

 

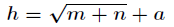
Among them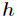For the number of hidden layer nodes,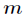For the number of input layer nodes,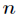For the number of output layer nodes,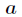by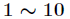Adjustment constant between.

 

 

3. Forward Transfer Subprocesses

 

Nodes are now set up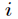Node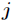The weights between them are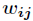Node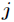The threshold is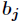The output value of each node is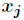And the output of each node

Value is based on the output value of all nodes in the upper layer, the weight value of the current node and all nodes in the upper layer, the threshold value of the current node and the activation function.

. The specific calculation method is as follows.

 

                    

 

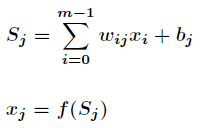
Among them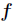In order to activate function, S-type function or linear function are generally selected.

 

The forward transfer process is relatively simple and can be calculated according to the above formula. In BP neural network, the input layer node has no threshold.

 

 

4. Reverse Transfer Subprocesses

 

Back-propagation of error signal is a complex sub-process in BP neural network, which is based on Widrow-Hoff learning rules. Assumed output layer

All results are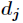The error function is as follows

 

                    

 

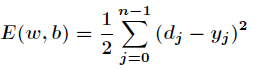
The main purpose of BP neural network is to revise weights and thresholds repeatedly so as to minimize the error function. Widrow-Hoff Learning Rules

By continuously adjusting the weights and thresholds of the network along the steepest descent direction of the sum of squares of relative errors, according to the gradient descent method, the weights vector

The correction is proportional to the gradient of E(w,b) at the current position, for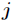There are two output nodes.

 

                    

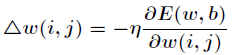
Suppose that the selected activation function is

 

                    

 

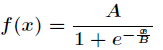
The derivative of activation function is obtained.

 

                   

 

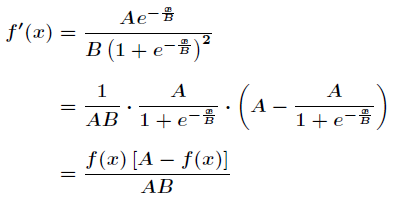
Next, we will focus onYes

 

                   

 

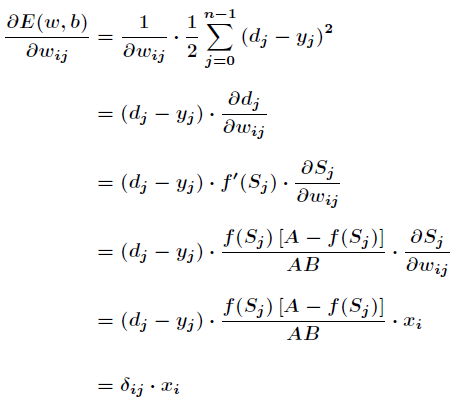
Among them are

                            

 

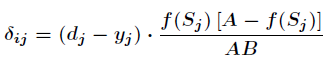
Similarly for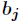Yes

 

                 

 

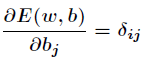
This is famous.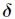Learning rules reduce errors in the actual and expected output of the system by changing the connection weights between neurons.

It is also called Widrow-Hoff learning rule or error-correcting learning rule.

  

The above is to calculate the adjustments of the weights between the hidden layer and the output layer, and the adjustments of the thresholds for the input layer, the hidden layer and the hidden layer.

Integer calculation is more complicated. hypothesis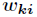Is the weight between the k-th node of the input layer and the i-th node of the hidden layer, then there is

 

                

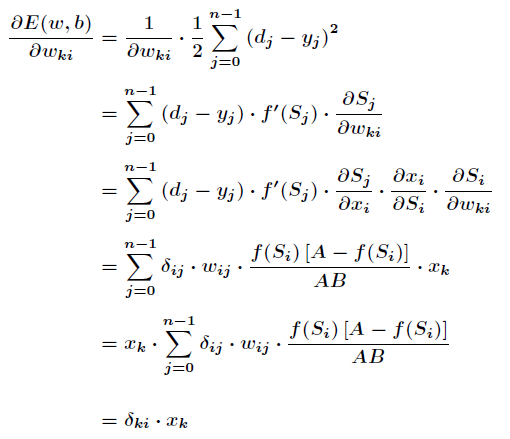
Among them are

 

                

 

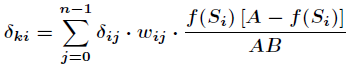
That's right.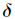Learn rules more deeply.

 

With the above formula, according to the gradient descent method, the weights and thresholds between the hidden layer and the output layer are adjusted as follows.

 

                

 

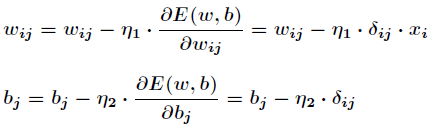
The weight and threshold adjustments between the input layer and the hidden layer are the same.

 

                

 

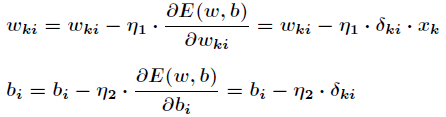
So far, the principle of BP neural network is basically finished.

 

 

5. Attentions of BP Neural Network

 

BP neural network is generally used to classify or approximate problems. If used for classification, the activation function usually chooses Sigmoid function or hard limit function.

Number, if used for function approximation, the output layer node uses a linear function, i.e..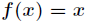

 

BP neural network can adopt incremental learning or batch learning when training data.

 

Incremental learning requires that the input mode should be random enough and sensitive to the noise of the input mode, that is, training for the input mode which changes dramatically.

The training effect is poor and suitable for on-line processing. Batch learning has no input mode order problem and good stability, but it is only suitable for offline processing.

 

Defects of standard BP neural network:

 

(1) It is easy to form local minima without obtaining global optimum.

There are many minimum values in BP neural network, so it is easy to fall into local minimum, which requires initial weights and thresholds.

The randomness of the initial weights and thresholds is good enough to be implemented randomly many times.

(2) The more training times, the lower learning efficiency and the slower convergence speed.

(3) The selection of hidden layer lacks theoretical guidance.

(4) There is a tendency to forget old samples when learning new samples during training.

   

   BPalgorithm Improvement:

 

(1) Increasing momentum terms

The momentum term is introduced to accelerate the convergence of the algorithm, i.e. the following formula

 

       

 

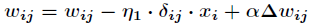
Momentum factor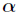General selection.

 

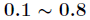(2) Adaptive adjustment of learning rate

(3) introducing steepness factor

 

Normally, BP neural network normalizes the data before training, which maps the data into smaller intervals, such as [0,1] or [-1,1].

 

 

6. C++ Implementation of BP Neural Network

 

The C++ files of BP neural network are as follows

 

   

 

BP.h:

1. #ifndef _BP_H_  
2. #define _BP_H_  
3.    
4. #include <vector>  
5.    
6. #define LAYER 3 // Three-Layer Neural Network  
7. #define NUM * 10 // Maximum number of nodes per layer  
8.    
9. #define A        30.0  
10. #define B. 10.0//A and B are parameters of S-type functions  
11. #define ITERS 1000 // Maximum number of training  
12. #define ETA_W 0.0035// Weight Adjustment Rate  
13. #define ETA_B 0.001//Threshold Adjustment Rate  
14. #define ERROR 0.002// Permissible Errors for a Single Sample  
15. #define ACCU 0.005// Permissible error per iteration  
16.    
17. #define Type double  
18. #define Vector std::vector  
19.    
20. struct Data  
21. {  
22.     Vector<Type> x;       //Input data  
23.     Vector<Type> y;       //output data  
24. };  
25.    
26. class BP{  
27.    
28. public:  
29.    
30.     void GetData(const Vector<Data>);  
31.     void Train();  
32.     Vector<Type> ForeCast(const Vector<Type>);  
33.    
34. private:  
35.    
36.     void InitNetWork();         //Initialize the network  
37.     void GetNums();             //Get the number of input, output, and hidden layer nodes  
38.     void ForwardTransfer();     //Forward Propagator Subprocess  
39.     void ReverseTransfer(int);  //Reverse Propagation Subprocess  
40.     void CalcDelta(int);        //Calculate the adjustments of w and b  
41.     void UpdateNetWork();       //Update weights and thresholds  
42.     Type GetError(int);         //Calculating the Error of a Single Sample  
43.     Type GetAccu();             //Calculating the Accuracy of All Samples  
44.     Type Sigmoid(const Type);   //Calculate the value of Sigmoid  
45.    
46. private:  
47.     int in_num;                 //Number of input layer nodes  
48.     int ou_num;                 //Number of Output Layer Nodes  
49.     int hd_num;                 //Number of Hidden Layer Nodes  
50.    
51.     Vector<Data> data;          //Input and output data  
52.    
53.     Type w[LAYER][NUM][NUM];    //Weights of BP Network  
54.     Type b[LAYER][NUM];         //Threshold of BP Network Node  
55.        
56.     Type x[LAYER][NUM];         //The output value of each neuron is transformed by S-type function, and the input layer is the original value.  
57.     Type d[LAYER][NUM];         //Record the value of delta in delta learning rules  
58. };  
59.    
60. #endif  //_BP_H_  

BP.cpp:

1. #include <string.h>  
2. #include <stdio.h>  
3. #include <math.h>  
4. #include <assert.h>  
5. #include "BP.h"  
6.   
7. //Obtain all training sample data  
8. void BP::GetData(const Vector<Data> _data)  
9. {  
10.     data = _data;  
11. }  
12.   
13. //Start training  
14. void BP::Train()  
15. {  
16.     printf("Begin to train BP NetWork!\n");  
17.     GetNums();  
18.     InitNetWork();  
19.     int num = data.size();  
20.   
21.     for(int iter = 0; iter <= ITERS; iter++)  
22.     {  
23.         for(int cnt = 0; cnt < num; cnt++)  
24.         {  
25.             //Layer 1 input node assignment  
26.             for(int i = 0; i < in_num; i++)  
27.                 x[0][i] = data.at(cnt).x[i];  
28.   
29.             while(1)  
30.             {  
31.                 ForwardTransfer();       
32.                 if(GetError(cnt) < ERROR)    //If the error is small, jump out of the loop for a single sample  
33.                     break;  
34.                 ReverseTransfer(cnt);    
35.             }  
36.         }  
37.         printf("This is the %d th trainning NetWork !\n", iter);  
38.   
39.         Type accu = GetAccu();  
40.         printf("All Samples Accuracy is %lf\n", accu);  
41.         if(accu < ACCU) break;  
42.     }  
43.     printf("The BP NetWork train End!\n");  
44. }  
45.   
46. //Predict the output value according to the trained network  
47. Vector<Type> BP::ForeCast(const Vector<Type> data)  
48. {  
49.     int n = data.size();  
50.     assert(n == in_num);  
51.     for(int i = 0; i < in_num; i++)  
52.         x[0][i] = data[i];  
53.       
54.     ForwardTransfer();  
55.     Vector<Type> v;  
56.     for(int i = 0; i < ou_num; i++)  
57.         v.push_back(x[2][i]);  
58.     return v;  
59. }  
60.   
61. //Get the number of network nodes  
62. void BP::GetNums()  
63. {  
64.     in_num = data[0].x.size();                         //Get the number of input layer nodes  
65.     ou_num = data[0].y.size();                         //Get the number of output layer nodes  
66.     hd_num = (int)sqrt((in_num + ou_num) * 1.0) + 5;   //Getting Number of Hidden Layer Nodes  
67.     if(hd_num > NUM) hd_num = NUM;                     //The number of hidden layers should not exceed the maximum setting  
68. }  
69.   
70. //Initialize the network  
71. void BP::InitNetWork()  
72. {  
73.     memset(w, 0, sizeof(w));      //Initialization weights and thresholds are 0, and random values can also be initialized.  
74.     memset(b, 0, sizeof(b));  
75. }  
76.   
77. //Forward transmission sub-process of working signal  
78. void BP::ForwardTransfer()  
79. {  
80.     //Calculating the Output Values of the Nodes in the Hidden Layer  
81.     for(int j = 0; j < hd_num; j++)  
82.     {  
83.         Type t = 0;  
84.         for(int i = 0; i < in_num; i++)  
85.             t += w[1][i][j] * x[0][i];  
86.         t += b[1][j];  
87.         x[1][j] = Sigmoid(t);  
88.     }  
89.   
90.     //Calculate the output value of each node in the output layer  
91.     for(int j = 0; j < ou_num; j++)  
92.     {  
93.         Type t = 0;  
94.         for(int i = 0; i < hd_num; i++)  
95.             t += w[2][i][j] * x[1][i];  
96.         t += b[2][j];  
97.         x[2][j] = Sigmoid(t);  
98.     }  
99. }  
100.   
101. //Calculating the Error of a Single Sample  
102. Type BP::GetError(int cnt)  
103. {  
104.     Type ans = 0;  
105.     for(int i = 0; i < ou_num; i++)  
106.         ans += 0.5 * (x[2][i] - data.at(cnt).y[i]) * (x[2][i] - data.at(cnt).y[i]);  
107.     return ans;  
108. }  
109.   
110. //Error Signal Reverse Transfer Subprocess  
111. void BP::ReverseTransfer(int cnt)  
112. {  
113.     CalcDelta(cnt);     
114.     UpdateNetWork();  
115. }  
116.   
117. //Calculating the Accuracy of All Samples  
118. Type BP::GetAccu()  
119. {  
120.     Type ans = 0;  
121.     int num = data.size();  
122.     for(int i = 0; i < num; i++)  
123.     {  
124.         int m = data.at(i).x.size();  
125.         for(int j = 0; j < m; j++)  
126.             x[0][j] = data.at(i).x[j];  
127.         ForwardTransfer();  
128.         int n = data.at(i).y.size();  
129.         for(int j = 0; j < n; j++)  
130.             ans += 0.5 * (x[2][j] - data.at(i).y[j]) * (x[2][j] - data.at(i).y[j]);  
131.     }  
132.     return ans / num;  
133. }  
134.   
135. //Calculate adjustment  
136. void BP::CalcDelta(int cnt)  
137. {  
138.     //Calculating delta Value of Output Layer  
139.     for(int i = 0; i < ou_num; i++)  
140.         d[2][i] = (x[2][i] - data.at(cnt).y[i]) * x[2][i] * (A - x[2][i]) / (A * B);  
141.     //Calculating delta Value of Implicit Layer  
142.     for(int i = 0; i < hd_num; i++)  
143.     {  
144.         Type t = 0;  
145.         for(int j = 0; j < ou_num; j++)  
146.             t += w[2][i][j] * d[2][j];  
147.         d[1][i] = t * x[1][i] * (A - x[1][i]) / (A * B);  
148.     }  
149. }  
150.   
151. //Adjust BP network according to the calculated adjustment amount  
152. void BP::UpdateNetWork()  
153. {  
154.     //Weight and Threshold Adjustment Between Implicit Layer and Output Layer  
155.     for(int i = 0; i < hd_num; i++)  
156.     {  
157.         for(int j = 0; j < ou_num; j++)  
158.             w[2][i][j] -= ETA_W * d[2][j] * x[1][i];   
159.     }  
160.     for(int i = 0; i < ou_num; i++)  
161.         b[2][i] -= ETA_B * d[2][i];  
162.   
163.     //Weight and Threshold Adjustment Between Input Layer and Implicit Layer  
164.     for(int i = 0; i < in_num; i++)  
165.     {  
166.         for(int j = 0; j < hd_num; j++)  
167.             w[1][i][j] -= ETA_W * d[1][j] * x[0][i];  
168.     }  
169.     for(int i = 0; i < hd_num; i++)  
170.         b[1][i] -= ETA_B * d[1][i];  
171. }  
172.   
173. //Calculating the value of Sigmoid function  
174. Type BP::Sigmoid(const Type x)  
175. {  
176.     return A / (1 + exp(-x / B));  
177. }  

Test.cpp:

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.    
5. #include "BP.h"  
6.    
7. using namespace std;  
8.    
9. double sample[41][4]=   
10. {   
11.     {0,0,0,0},   
12.     {5,1,4,19.020},   
13.     {5,3,3,14.150},   
14.     {5,5,2,14.360},   
15.     {5,3,3,14.150},   
16.     {5,3,2,15.390},   
17.     {5,3,2,15.390},   
18.     {5,5,1,19.680},   
19.     {5,1,2,21.060},   
20.     {5,3,3,14.150},   
21.     {5,5,4,12.680},   
22.     {5,5,2,14.360},   
23.     {5,1,3,19.610},   
24.     {5,3,4,13.650},   
25.     {5,5,5,12.430},   
26.     {5,1,4,19.020},   
27.     {5,1,4,19.020},   
28.     {5,3,5,13.390},   
29.     {5,5,4,12.680},   
30.     {5,1,3,19.610},   
31.     {5,3,2,15.390},   
32.     {1,3,1,11.110},   
33.     {1,5,2,6.521},   
34.     {1,1,3,10.190},   
35.     {1,3,4,6.043},   
36.     {1,5,5,5.242},   
37.     {1,5,3,5.724},   
38.     {1,1,4,9.766},   
39.     {1,3,5,5.870},   
40.     {1,5,4,5.406},   
41.     {1,1,3,10.190},   
42.     {1,1,5,9.545},   
43.     {1,3,4,6.043},   
44.     {1,5,3,5.724},   
45.     {1,1,2,11.250},   
46.     {1,3,1,11.110},   
47.     {1,3,3,6.380},   
48.     {1,5,2,6.521},   
49.     {1,1,1,16.000},   
50.     {1,3,2,7.219},   
51.     {1,5,3,5.724}   
52. };   
53.    
54. int main()  
55. {  
56.     Vector<Data> data;  
57.     for(int i = 0; i < 41; i++)  
58.     {  
59.         Data t;  
60.         for(int j = 0; j < 3; j++)  
61.             t.x.push_back(sample[i][j]);  
62.         t.y.push_back(sample[i][3]);  
63.         data.push_back(t);  
64.     }  
65.     BP *bp = new BP();  
66.     bp->GetData(data);  
67.     bp->Train();  
68.    
69.     while(1)  
70.     {  
71.         Vector<Type> in;  
72.         for(int i = 0; i < 3; i++)  
73.         {  
74.             Type v;  
75.             scanf("%lf", &v);  
76.             in.push_back(v);  
77.         }  
78.         Vector<Type> ou;  
79.         ou = bp->ForeCast(in);  
80.         printf("%lf\n", ou[0]);  
81.     }  
82.     return 0;  
83. }  

 

Makefile:

1. Test : BP.h BP.cpp Test.cpp  
2.     g++ BP.cpp Test.cpp -o Test  
3.    
4. clean:  
5.     rm Test