Catalogue of series articles
Preorder traversal: Root - > left - > right
Middle order traversal: left - > root - > right
Post order traversal: left - > right - > root
1, Middle order, pre order and post order traversal
Middle order traversal of binary tree: traverse the tree by accessing the left subtree - root node - right subtree. When accessing the left subtree or right subtree, we traverse in the same way until we traverse the whole tree. Therefore, the whole traversal process has the nature of recursion. We can directly simulate this process with recursive functions.


**Medium order traversal**
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var inorderTraversal = function(root) {
let res=[];
const inorder=(root)=>{
if(!root) return;
inorder(root.left);
res.push(root.val);
inorder(root.right);
}
inorder(root)
return res
};
**Preorder traversal**https://leetcode-cn.com/problems/binary-tree-preorder-traversal/submissions/
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
let res=[];
const inorder=(root)=>{
if(!root) return;
res.push(root.val);
inorder(root.left);
inorder(root.right);
}
inorder(root)
return res
};
**Postorder traversal**https://leetcode-cn.com/problems/binary-tree-postorder-traversal/submissions/
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var postorderTraversal = function(root) {
let res=[];
const inorder=(root)=>{
if(!root) return;
inorder(root.left);
inorder(root.right);
res.push(root.val);
}
inorder(root)
return res
};
2, Search the k-th largest binary tree
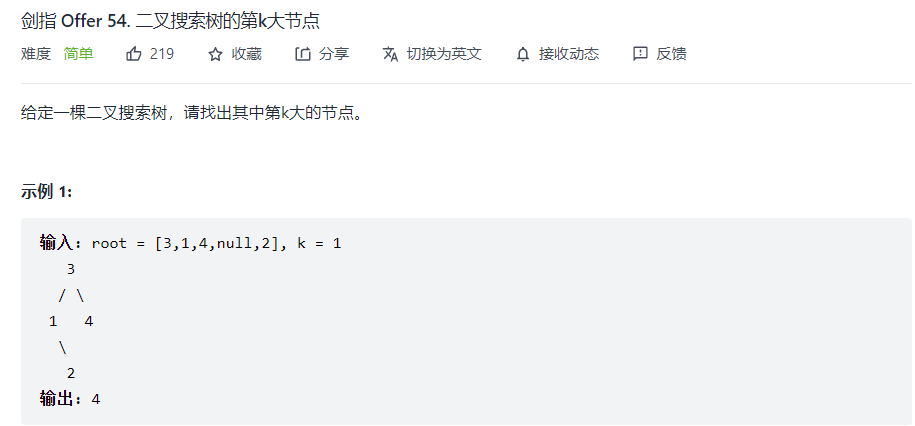
The binary search tree is traversed in middle order to get an incrementally sorted sequence
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} k
* @return {number}
*/
var kthLargest = function(root, k) {
let res=[]
const insort=(root)=>{
if(!root)return
insort(root.left);
res.unshift(root.val);
insort(root.right);
}
insort(root);
return res[k-1]
};
3, Next node of binary tree
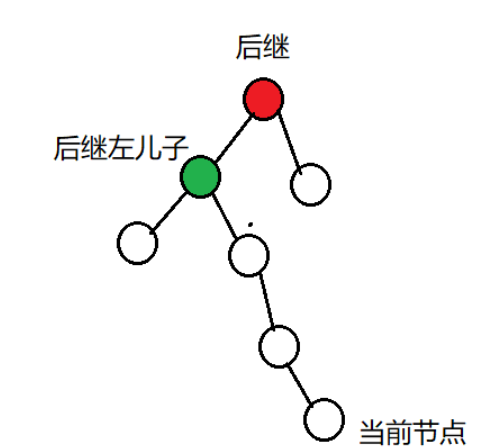
Title: given one node of a binary tree, please find the next node of the middle order traversal sequence.
- The node has a right subtree: the next node is the leftmost child node of the right subtree
- If the node does not have a right subtree (look up along its parent node to find the first node that is the left son of its parent node, and the parent node of the node is the successor of the current node)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
function GetNext(pNode){
if(pNode.right){
pNode=pNode.right;
while(pNode.left){
pNode=pNode.left;
}
return pNode
}
while(pNode.next){
if(pNode===pNode.next.left){
return pNode.next//Represents the parent node up
}
pNode=pNode.next
}
return null
}
4, Maximum depth of binary tree
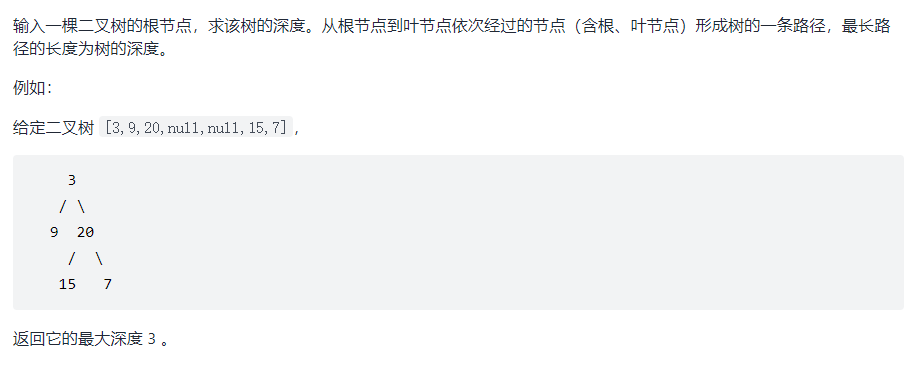
This problem is very simple. If a node is not found, it returns 0. If a node is found, it recurses the function + 1. It recurses several times in several layers. Math.max is to compare two numbers, who is bigger
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
if(!root)return 0;
return Math.max(maxDepth(root.left),maxDepth(root.right))+1
};
5, Image of binary tree

Problem solving ideas:
Start from the root node, recursively traverse the tree, and flip from the leaf node to get the image. If the left and right subtrees of the currently traversed node root have been flipped to get the image, we only need to exchange the positions of the two subtrees to get the image of the whole subtree with root as the root node.
The so-called recursion is to assume that the part to be recursively entered has been processed, and the deep processing is carried out first. The data in the deep is given from the shallow part, and the return value obtained from the shallow part is the value of the last returned function.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var mirrorTree = function(root) {
//Judge root node
if (root == null) {
return null;
}
//Swap left and right subtrees
const left=mirrorTree(root.left);
const right=mirrorTree(root.right);
root.left=right;
root.right=left;
return root
};
6, Symmetric binary tree

Problem solving idea: recursion
- Two empty trees, true
- There is only one empty tree, false
- Node values are equal
- The left subtree of left and the right subtree of right are mirror images
- The right subtree of left and the left subtree of right are mirror images
.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
if(!root)return true;
const check=(left,right)=>{
if (left == null&&right==null) {
return true;//Two empty trees, true
}
if (left == null||right==null) {
return false;//There is only one empty tree, false
}
return(left.val==right.val&&check(left.left,right.right)&&check(left.right,right.left))//Conditions for mirroring: the node values are equal, the left subtree and right subtree of left are mirrored, and the right subtree of left and right are mirrored
}
return check(root.left,root.right)
};
7, Balanced binary tree
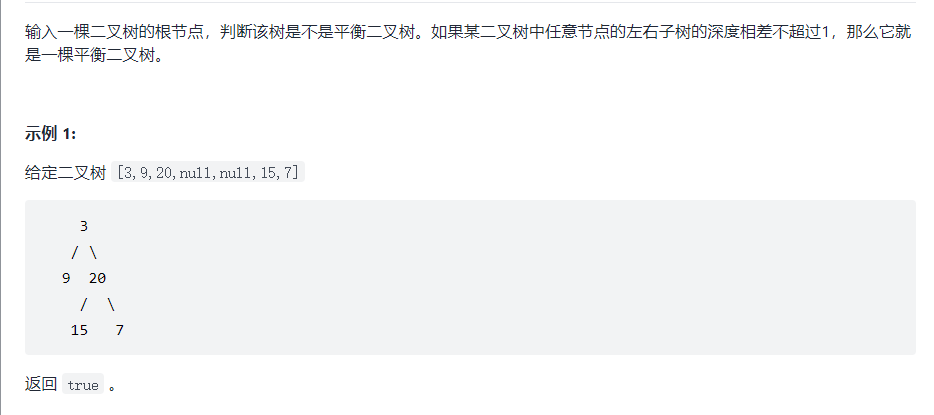
In fact, it is an improvement on the basis of finding the deepest length of binary tree. Two conditions judge it false - (1) the length difference in any function at the same recursive level is greater than one return - 1; (2) In
left==-1||right==-1 means that when recursing to the shallowest place, if the difference is greater than 1, it will also return - 1
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isBalanced = function(root) {
const check=(root)=>{
if(!root)return 0;
const left=check(root.left);
const right=check(root.right);
if(left==-1||right==-1||Math.abs(left-right)>1){
return -1;
}
return Math.max(left,right)+1
}
return check(root)!=-1
};
8, Print binary tree from top to bottom (sequence traversal BFS cycle)

Problem solving ideas:
(1) Special case handling: when the root node is empty, an empty list [] is returned;
(2) Initialization: print result list res = [], queue containing root node = [root];
(3) Jump out when the queue is empty;
(4) Create a temporary list tmp to store the print results of the current layer;
(5) Current layer print cycle: the number of cycles is the number of nodes in the current layer (i.e. queue length);
(6) Out of line: the first element of the team is out of line (shift operation), which is recorded as node;
(7) Add node.val to the tail of tmp;
(8) Add child node: if the left (right) child node of node is not empty, the left (right) child node will be added to the queue;
(9) Add the current layer result tmp to res.
(10) Return to the print result list res.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function(root) {
let res=[];
let queue=[];
if(!root)return [];
queue.push(root);
while(queue.length){
let len=queue.length
let temp=[]
for(var i=0;i<len;i++){
let node=queue.shift();
temp.push(node.val);
if (node.left){
queue.push(node.left);
}
if(node.right){
queue.push(node.right);
}
}
res.push(temp)
}
return res
};