Binary tree C language implementation version of data structure
What is a tree?
A Tree is a finite set of N nodes. It can be an empty Tree (n=0) or an empty Tree. Non empty trees have the following characteristics:
- There is and only one node called root
- In addition to the root node, other nodes can be divided into m (M > 0) disjoint finite sets T1,T2,..., Tm, in which each set itself is a tree and is called the subtree of the root.
Basic terms of trees
The look of a tree
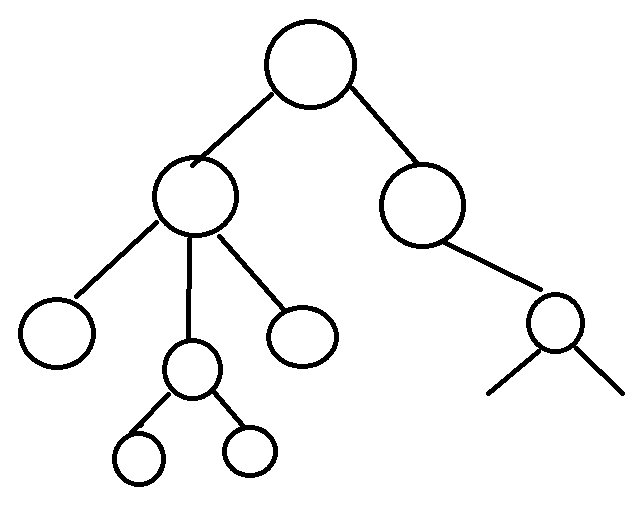
The following definitions come from the textbook named data structure C language version | 2nd Edition compiled by Yan Weimin and others. Then added some of their own understanding.
-
Node: an independent cell in a tree. Contains a data element and several branches to its subtree.
-
Node degree: the subtree owned by a node is called node degree. There are several sons under the father.
-
Tree degree: the degree of the tree is the maximum degree of each node in the tree. The degree of the tree depends on the number of sons at the node with the most sons in the whole family.
-
Leaves: nodes with zero degrees are called leaves. There are no other nodes after the node. Such a node is a leaf
-
Non terminal node: a node whose degree is not zero is called a non terminal node. In addition to the root node, non terminal nodes are also called internal nodes.
-
Parents and children: the root of the subtree of the node is called the child of the node (son, because it sounds strange to say daughter). Accordingly, the node is called the child's parents (father or mother)
-
Brothers: children of the same parents are called brothers or sisters to each other.
-
Ancestor: all nodes experienced from the root node to the node. All nodes before a node are called its ancestors.
-
Descendant: any node summarized in the subtree with a node as the root node is called the descendant of the node.
-
Hierarchy: the hierarchy of a node is defined from the root. The root is the first layer and the children of the root are the second layer. The level of any node in the tree is equal to the level of its parent node plus 1.
-
Cousins: the nodes of parents on the same floor are cousins to each other.
-
Depth of tree: the maximum level of nodes in the tree is called the depth or height of the tree. The level from the root to the node farthest from it is the depth of the tree.
-
Ordered tree and unordered tree: if the subtrees of the nodes in the tree are regarded as ordered from left to right (that is, they cannot be interchanged), the tree is called ordered tree, otherwise it is called unordered tree. In an ordered tree, the root of the leftmost subtree is called the first child, and the rightmost subtree is called the last child.
-
Forest: it is a collection of m (m > = 0) unrelated trees. Literally, it is a collection of many trees.
Definition of binary tree
What the cells of a binary tree look like
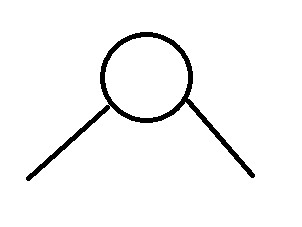
Properties of binary tree
- The binary tree itself is also a tree
- There is only one root node
- The other nodes except the root node are divided into two unrelated subsets T1 and T2, which are called the left subtree and right subtree of T respectively, and T1 and T2 are binary trees themselves.
- The tree can have any number of sub trees, and each node of a binary tree has at most two sub trees.
- The subtree of a binary tree can be divided into left and right, and its order cannot be reversed arbitrarily.
Implementation of binary tree
Theoretical knowledge is finished directly by reading a book. It mainly depends on the implementation process of binary tree.
Binary tree structure form
typedef struct Node
{
int data;
struct Node* leftChild;
struct Node* rightChild;
}Node,*pNode;
Use typedef as an alias. After all, C + + is used to it.
Creation of binary tree node
pNode creatNode(int data)
{
pNode newNode = (pNode)malloc(sizeof(Node));
assert(newNode); //Assert
newNode->data = data;
newNode->leftChild = NULL;
newNode->rightChild = NULL;
return newNode;
}
This creation method is the same as that of the two-way circular linked list, but the subsequent use is different.
Insert node
void insertNode(pNode fatherNode, pNode leftChild, pNode rightChild)
{
fatherNode->leftChild = leftChild;
fatherNode->rightChild = rightChild;
}
This kind of insertion seems very stupid, but it's easy to understand. Directly, it is the units of the binary tree that practice one by one.
Recursive traversal of binary tree
Binary tree is a little different from other data structures. Generally, when using binary tree, it is only stored, so you can know how to store and traverse.
There are three traversal formats for binary trees, namely:
- Pre order: from three to three, print the root node first, then the left subtree node, and finally the right subtree node, referred to as the root node
- Middle order: from three to three, print the left subtree node first, then the root node, and finally the right subtree node, referred to as left root right
- Post order: three by three, print the left subtree node first, then the right subtree node, and finally the root node, referred to as the left and right roots
Understand through cases:
Now there is a binary tree:
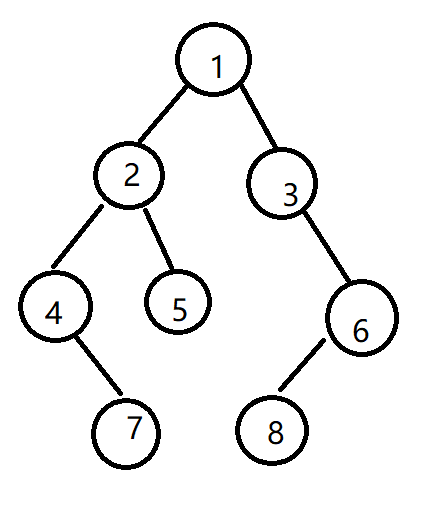
Manual writing and printing results: three and three
Preamble:
1, 123 2, 12453 3, 124753 4, 12475368 Final result: 12475368
Middle order:
1, 213 2, 42513 3, 472513 4, 47251386 Final result: 47251386
Post order:
1, 231 2, 45231 3, 745231 4, 7452631 5, 74528631 Final result: 74528631
Preorder traversal
If you understand the first two, you will understand naturally. The idea is very simple. If the parent node is empty at the beginning, directly end the whole function. If it is not empty, print the data in the current node, and then call print again with the left subtree of the current node as a function parameter_ Front function, and then take the right subtree of the current node as the function parameter and call print again_ For the front function, the left side completes the left side, the right side completes the right side, and then it is left and right according to the root. Note that the sorting of the three lines of code is also arranged in the order around the root.
void print_front(pNode fatherNode)
{
if (fatherNode == NULL)
return;
printf("%d ", fatherNode->data);
print_front(fatherNode->leftChild);
print_front(fatherNode->rightChild);
}
Medium order traversal
The middle order traversal is almost the same as the previous pre order traversal, except that the order of the key three lines of code is changed, and the binary tree is printed in the way of left root and right.
void print_mid(pNode fatherNode)
{
if (fatherNode == NULL)
return;
print_mid(fatherNode->leftChild);
printf("%d ", fatherNode->data);
print_mid(fatherNode->rightChild);
}
Postorder traversal
The idea of traversal is the same as that of the previous traversal method. The order of three lines of code has changed. It is worth noting that the left must be on the left of the right.
void print_last(pNode fatherNode)
{
if (fatherNode == NULL)
return;
print_last(fatherNode->leftChild);
print_last(fatherNode->rightChild);
printf("%d ", fatherNode->data);
}
Non recursive traversal binary tree
Traversing the binary tree recursively is obvious, and the code is very simple. The following is traversal without recursion, so you need a stack to store the pointer traversing the node, so that the pointer can go back. The code of preorder traversal is 99% similar to that of preorder traversal, but the postorder traversal is a little troublesome.
Preorder traversal
Idea: if the current parent node is empty, directly end the whole function. If it is not empty, prepare a stack (in practical application, it is generally represented by an array. Generally, a stack structure of hundreds of lines will not be written). Stack to store the nodes that the moving pointer passes through. Go to the end and print out of the stack, then find the right, and then go to the end and print out of the stack, all the way through the cycle. Look directly at the code comments
void print_front_while(pNode fatherNode)
{
if (fatherNode == NULL)
return;
//Prepare a stack and implement it with an array
pNode stack[100];
int top = -1; //Stack top tag
pNode pMove = fatherNode; //Define a moving pointer to traverse the binary tree
while (top != -1 || pMove != NULL) //Traverse the entire binary tree
{
while (pMove != NULL) //Move the pointer to the end of the left subtree
{
printf("%d ", pMove->data); //Print while walking
stack[++top] = pMove; //Record nodes passed
pMove = pMove->leftChild; //Go left
}
if (top != -1) //Judge whether the stack is empty. If the stack is not empty, it means that the binary tree is not finished
{
pMove = stack[top--]; //Out of stack
pMove = pMove->rightChild; //Find the node on the right
}
}
}
Medium order traversal
void print_mid_while(pNode fatherNode)
{
if (fatherNode == NULL)
return;
pNode stack[100]; //Prepare a stack and implement it with an array
int top = -1;
pNode pMove = fatherNode;
while (top != -1 || pMove != NULL) //Traverse the entire binary tree
{
while (pMove != NULL) //Go to the end of the left subtree of the binary tree
{
//It's no longer printing while walking
stack[++top] = pMove; //Record nodes passed
pMove = pMove->leftChild; //Go left
}
if (top!=-1) //Judge whether the stack is empty. If it is not empty, it indicates that the binary tree has not been completed
{
pMove = stack[top--]; //Out of the stack, move the pointer back
printf("%d ", pMove->data); //print data
pMove = pMove->rightChild; //Find the right node
}
}
}
Postorder traversal
Post order traversal is a little more troublesome, because there is a problem of secondary stacking, so the code is more complex than the previous one.
void print_last_while(pNode fatherNode)
{
if (fatherNode == NULL)
return;
pNode stack[100]; //Prepare a stack and implement it with an array
int top = -1;
pNode pMove = fatherNode;
pNode pMemory = NULL; //Define a recorded pointer. The recorded pointer does not need to print the data in the node again
while (pMove != NULL) //Move the pointer to the end of the left subtree
{
stack[++top] = pMove; //Stack and record the nodes passed by the moving pointer
pMove = pMove->leftChild; //Move the pointer to the left
}
while(top != -1) //top is not equal to - 1, indicating that there is a recorded pointer in the stack
{
pMove = stack[top--]; //Out of stack
//Judge whether the current node has a right subtree or a pointer that has been recorded
if (pMove->rightChild == NULL || pMove->rightChild == pMemory)
{
printf("%d ", pMove->data); //print data
pMemory = pMove; //Record pointer
}
else
{
//If the right subtree has data or no pointer has been recorded, put the current pointer on the stack
stack[++top] = pMove;
pMove = pMove->rightChild; //Then enter the right subtree
while (pMove != NULL) //Go to the end of the left subtree of the right subtree
{
stack[++top] = pMove;
pMove = pMove->leftChild;
}
}
}
}
Main function test
int main()
{
pNode node1 = creatNode(9);
pNode node2 = creatNode(8);
pNode node3 = creatNode(7);
pNode node4 = creatNode(6);
pNode node5 = creatNode(5);
pNode node6 = creatNode(4);
pNode node7 = creatNode(3);
pNode node8 = creatNode(2);
pNode node9 = creatNode(1);
insertNode(node1, node2, node3);
insertNode(node2, NULL, node4);
insertNode(node3, node6, NULL);
insertNode(node4, node5, node8);
insertNode(node6, node9, node7);
/*
one nine
two eight seven
three N six four N
four five two one three
*/
//Pre order printing
printf("Pre order print results:\n");
print_front(node1);
printf("\n");
print_front_while(node1);
//Medium order printing
printf("\n Middle order print results:\n");
print_mid(node1);
printf("\n");
print_mid_while(node1);
//Post order printing
printf("\n Post order print results:\n");
print_last(node1);
printf("\n");
print_last_while(node1);
return 0;
}
Output results:
Pre order print results: 9 8 6 5 2 7 4 1 3 9 8 6 5 2 7 4 1 3 Middle order print results: 8 5 6 2 9 1 4 3 7 8 5 6 2 9 1 4 3 7 Post order print results: 5 2 6 8 1 3 4 7 9 5 2 6 8 1 3 4 7 9