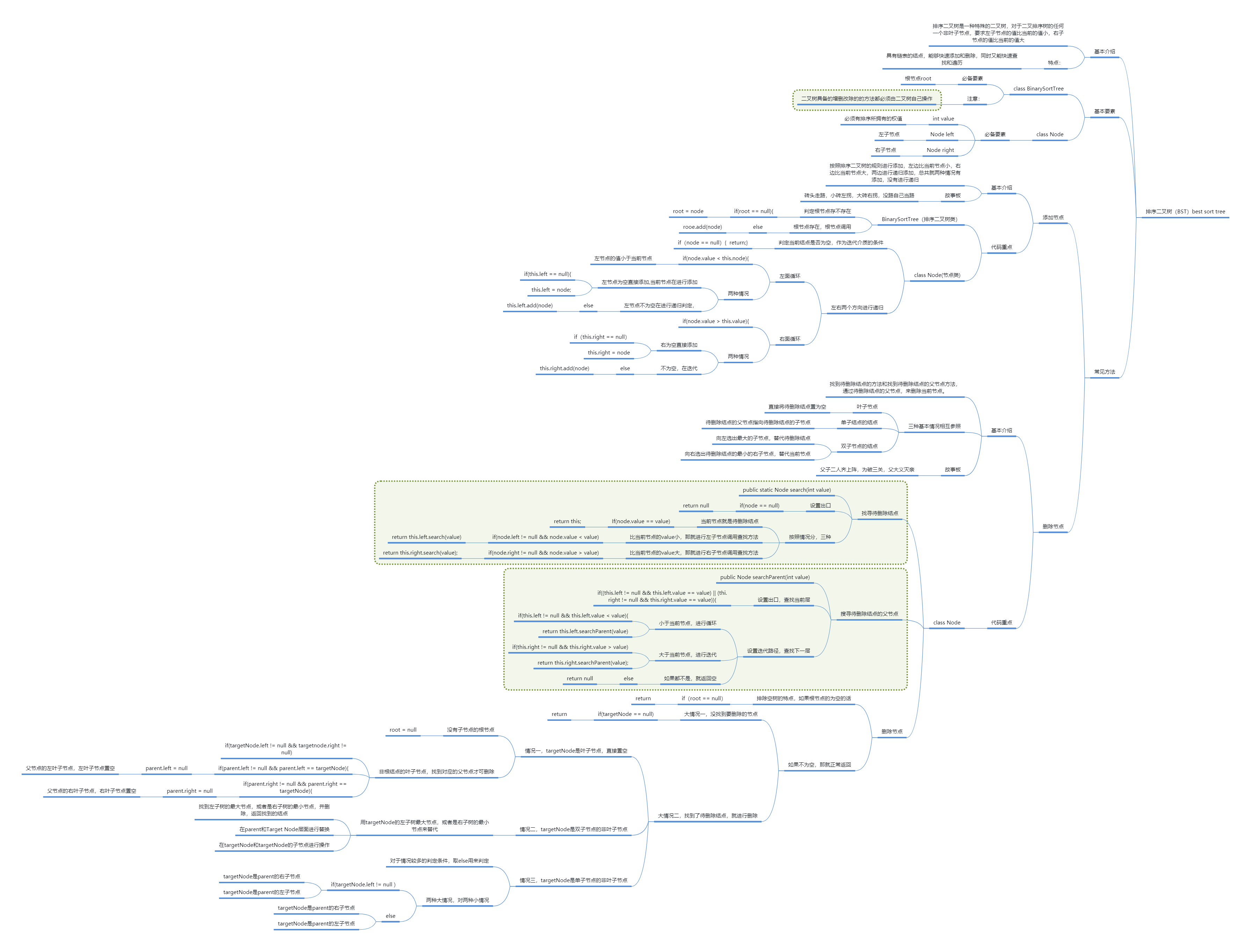
Binary sort tree (BST)

Introduction of topics

1. Requirements: efficient query and addition of sequence {7, 3, 10, 12, 1, 5, 9}.

• Analysis:
  • Use array: the array is unsorted, and the advantages are added directly at the end. It is fast and slow to find: the array is sorted, and binary search is fast, but adding elements and inserting them in the middle makes the array move backward as a whole, which is slow.
  • Using linked storage linked list: adding and deleting nodes is fast, but finding nodes is slow
  • Using binary sorting tree: fast retrieval speed, fast search speed, at the same time than that with adding and modifying.

The introduction of binary sort tree

1. Binary Sort tree: BST (Binary Sort() Search Tree). For any non leaf node of the Binary Sort tree, the value of the left sub node is required to be smaller than the value of the current node, and the value of the right sub node is required to be larger than the current value. (small on the left and large on the right)
2. Special note: if the added value is the same as a certain point, it will be placed in the left sub node to ensure that there are no two same nodes in the same layer, which are left and right nodes.

Add node code implementation:

class BinarySortTree

public void add(Node node) {
        if (root == null) {
            root = node;
        } else {
            root.add(node);
        }
    }

class Node

public void add(Node node){
        if (node == null){
            return;
        }
        if(node.value < this.value){
            if (this.left == null){
                this.left = node;
            }else{
                this.left.add(node);
            }
        }else{
            if (this.right == null){
                this.right = node;
            }else{
                this.right.add(node);
            }
        }
    }

Summary and analysis:

1. In addition to the formal parameter list and the object of the calling method, a method operation object has no need to add another parameter object root to handle the addition method, and directly manipulate the this of the current calling method.
2. When calling the member variables of left and right child nodes, it is necessary to determine whether the left and right child nodes are empty.

Delete node - code implementation:

Thinking analysis

1. Three situations:
   • Delete leaf node
   • Delete a node with only one subtree
   • Delete a node with two subtrees
2. Thought analysis:

   1. Delete leaf node

      1. Find the parent node of the targetNode to be deleted. There are two cases
         • No parent, root
         • Parent node, non root node
      2. Determine whether the targetNode is the left or right child of the parent
         • Left child: parent.left = null
         • Right child: parent.right = null

   2. Delete a node with a subtree

      1. Find parent of targetNode
      2. Determine whether targetNode is the left or right child of the parent node, and whether the child of targetNode is the left or right child of targetNode;
         • targetNode is the left child node of the parent. targetNode has only the left child tree, parent.left = targetNode.left;
         • targetNode is the left child node of the parent. targetNode has only the right child tree. parent.left = targetNode.right:
         • targetNode is the right child of the parent. targetNode has only the left child tree. parent.right = targetNode.left;
         • targetNode is the right child of the parent. targetNode has only the right child tree, parent.right = targetNode.right;

   3. Two subtrees to the right of the deleted target node TargetNode

      • Find the parent of the TargetNode to be deleted
      • Determine whether the TargetNode of the node to be deleted is the left node or the right node of the parent
      • TargetNode is the left node of parent. Select the largest node from the left subtree of TargetNode to replace TargetNode, or find the smallest node from the right subtree to replace TargetNode
      • TargetNode is the right node of parent. Select the largest node from the left subtree of TargetNode to replace TargetNode and delete it; or select the smallest node from the right subtree of TargetNode to replace TargetNode.

code implementation

1. Find the parent node of the node to be deleted
   class Node: find the corresponding node of the node to be deleted

public Node search(int value){
        if (this == null){
            return null;
        }
        if (value == this.value){
            return this;
        }else if(value < this.value){
            //If the value of the lookup is less than the value of the current node, recursion is made to the left
            //There is another problem: I don't know, but the front pointer memory doesn't exist. It may be zero
            if (this.left == null){
                return null;
            }
            return this.left.search(value);
        }else{
            //If the current value is greater than the value of the current node, recurse to the right
            //Problem: do not know whether the right child node exists
            if (this.right == null){
                return null;
            }
            return this.right.search(value);
        }
    }
    //Find the parent node of the node to be deleted

Find the parent node of the node to be deleted

/**
 *
 * @param value Node value to find
 * @return  Return the parent node of the node to be deleted. If not, return null
 */
public Node searchParent(int value){
    //If the current node is the parent node to be returned, the child node is the node to be searched
    if ((this.left != null && this.left.value == value)
            || (this.right != null && this.right.value == value)){
        return this;
    }else if(this.left != null && value < this.value){
        return this.left.searchParent(value);
        //If the returned node is not the current node, it means that the returned node is the left child node or the right child node,
        //Therefore, it should be called by the left child node or the right child node
    }else if(this.right != null && value >= this.value){
        return this.right.searchParent(value);
    }else {
        return null;
    }
}

Delete the largest node of the left subtree or the smallest node of the right subtree of the target Node

/**
     * Find the minimum value of the current subtree and delete the node at the same time
     * @param node node Incoming node (the root node of the left binary sort tree)
     * @return Returns the minimum Node Z of the binary sort tree with Node as the root Node
     * Personal opinion: return to the minimum node, and then delete
     */
    public Node delRightTreeMin(Node node){
        Node target = node;
        while (target.left != null){
            target = target.left;
        }
        Node temp = target;
        //The target of the exit loop points to the minimum node
        delNode(target.value);
        return target;
        //If the minimum value is found, the node is returned
    }

class BestSearchTree

//Find nodes to delete
    public Node search(int value){
        if (root == null){
            return null;
        }else{
            return root.search(value);
        }
    }
    //Find the parent of the node to delete
    public Node searchParent(int value){
        if(root == null){
            return null;
        }else{
            return root.searchParent(value);
        }
    }

The second part is classified and deleted according to the situation

public void delNode(int value){
        if (root == null){
            return ;
        }else{
            //1. It is required to find the node targetNode to be deleted first
            Node targetNode = search(value);
            //2. If the node to be deleted is not found
            if (targetNode == null){
                return;
            }
            //Case 1: there is no parent node, and the root node is the point to be found
            if ((root.left == null && root.right == null) && root == targetNode){
                root = null;
                return;
            }
                if (parent.left != null && parent.left == targetNode){
                    parent.left = null;
                }else if(parent.right != null && parent.right == targetNode){
                    parent.right = null;
                }
            }else if(targetNode.left != null && targetNode.right != null){
                Node minNode = delRightTreeMin(targetNode.right);
                if (parent.left != null && parent.left == targetNode){
                    parent.left = minNode;
                }else if(parent.right != null && parent.right == targetNode){
                    parent.right = minNode;
                }
                //Delete at the level of the parent node,
                minNode.left = targetNode.left;
                minNode.right = targetNode.right;
                //Operations at the child node level
          }else{
                //Case 4: delete only one subtree
                if (targetNode.right != null){
                    //Only left subtree, right subtree is empty
                    if ( parent.left == targetNode){
                        parent.left = targetNode.right;
                    }
                    if ( parent.right == targetNode){
                        parent.right = targetNode.right;
                    }
                }else{
                    if ( parent.left == targetNode){
                        parent.left = targetNode.left;
                    }
                    if (parent.right == targetNode){
                        parent.right = targetNode.left;
                    }
                }
            }

        }
    }

Analysis and summary

1. Tip: two way search, find the node to be deleted and the parent node of the node to be deleted at the same time, which is more convenient for deletion
2. In the sequential binary tree, to delete the non leaf node of the twin node, replace it with the maximum value of the left subtree or the minimum value of the right subtree, find the corresponding replacement value, delete it, and then replace the target node to be deleted
3. For more complex conditions, else is used instead of if()
4. Mind mapping