Binary search basis
1. Preface
In the past, I always felt that I had to go through all the concepts before I could start to brush the questions. I didn't know that practice was the shortcut to master knowledge, rather than forgetting to recite it. To learn knowledge, we need to settle down and go step by step, otherwise we will be punished for swallowing at a critical moment in the future.
So don't think so much. Just start with a simple binary search. However, although the dichotomy idea is simple, the details should be handled with extra care, otherwise it will easily lead to a dead circle.
2. Conceptual core
Ordered, half search, time complexity O(logN)
3. Algorithm template
Usually, our algorithm problems do not directly let us use dichotomy to find a number. We need to change it according to the actual situation.
Dichotomous questions are usually divided into two types:
- The first is to find the first subscript that meets the conditions, that is, 00001111 finds the first 1
- The second is to find the last subscript that meets the condition, that is, 11110000 finds the last 1
/*Template 1 (0 on the left and 1 on the right), find the first 100001111
* check(mid)It means to find '1'. At this time, the mid may be any '1' on the right,
* That is, we can't determine whether the mid is the first '1', so we can't write it when narrowing to the left
* r=mid-1,To write r=mid;
* Similarly, in the else case, '1' is not found, so the range is narrowed to the right. Because mid certainly does not meet the conditions, l=mid+1
*/
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
/*Template 2 (1 on the left and 0 on the right), find the last 111110000
* check(mid)It means to find '1'. At this time, the mid may be any '1' on the left,
* That is, we can't determine whether the mid is the last '1', so we can't write it when narrowing to the right
* l=mid+1,To be written as l=mid;
* Similarly, in the else case, '1' is not found, so the range is narrowed to the left. Because mid certainly does not meet the conditions, r=mid-1
*/
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1; //Add 1 to avoid dead cycle eg:10
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
4.Leetcode binary basic topic
Train of thought analysis:
Usually, the square root of an integer is an infinite acyclic decimal. According to the meaning of the question, we should return an integer less than or equal to the square root. In other words, we only need to find the largest integer from the integers less than or equal to the square root, which conforms to the model of 11110000 finding the last 1, that is, template 2.
Finally, pay attention to the data range.
class Solution {
public:
int mySqrt(int x) {
long long l = 0, r = x;
while (l < r) {
long long mid = l + r + 1 >> 1;
if (mid * mid <= (long long)x) l = mid;
else r = mid - 1;
}
return l;
}
};
Train of thought analysis:
There are no duplicate elements from the meaning, so template 1 and template two can be used. Here, special consideration should be given to the case that the array is empty or the search element is less than or greater than all array elements.
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int len = nums.size();
if (len == 0) return 0;
if (nums[len - 1] < target) return len;
if (nums[0] > target) return 0;
int l = 0, r = len - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return l;
}
};
34. Find the first and last position of an element in a sorted array
Train of thought analysis:
This idea is very clear. First use the template 00001111 to find the first 1; Then start from the first 1 found and use template 2 11110000 to find the last 1.
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int len = nums.size();
if (len == 0) return {-1, -1};
vector<int> vec;
int l = 0, r = len - 1, st = 0, ed = 0;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
if (nums[l] == target) {
st = l;
int low = st, high = len - 1;
while (low < high) {
int mid = low + high + 1 >> 1;
if (nums[mid] > target) high = mid - 1;
else low = mid;
}
ed = low;
vec.push_back(st);
vec.push_back(ed);
} else {
vec.push_back(-1);
vec.push_back(-1);
}
return vec;
}
};
74. Search two-dimensional matrix
Train of thought analysis:
Simple two point search, using template 1, template two can be. The key is the representation of two-dimensional matrix subscripts.
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.size() == 0 || matrix[0].size() == 0) return false;
int n = matrix.size();
int m = matrix[0].size();
int l = 0 ,r = n * m - 1;
while(l < r){
int mid = l + r >> 1;
if(matrix[mid/m][mid%m] >= target) r = mid;
else l = mid + 1;
}
if(matrix[r/m][r%m] == target) return true;
return false;
}
};
153. Find the minimum value in the rotation sort array
Train of thought analysis:
From the meaning of the question, the rotation array is shown in the figure. Finding the minimum value is equivalent to finding the first 1 of 00001111. We only need to set the judgment condition to be less than or equal to the last value of the array. At this time, it is known from the figure on the left that it is greater than the last value of the array, set it to 0, and set it to 1 on the right.
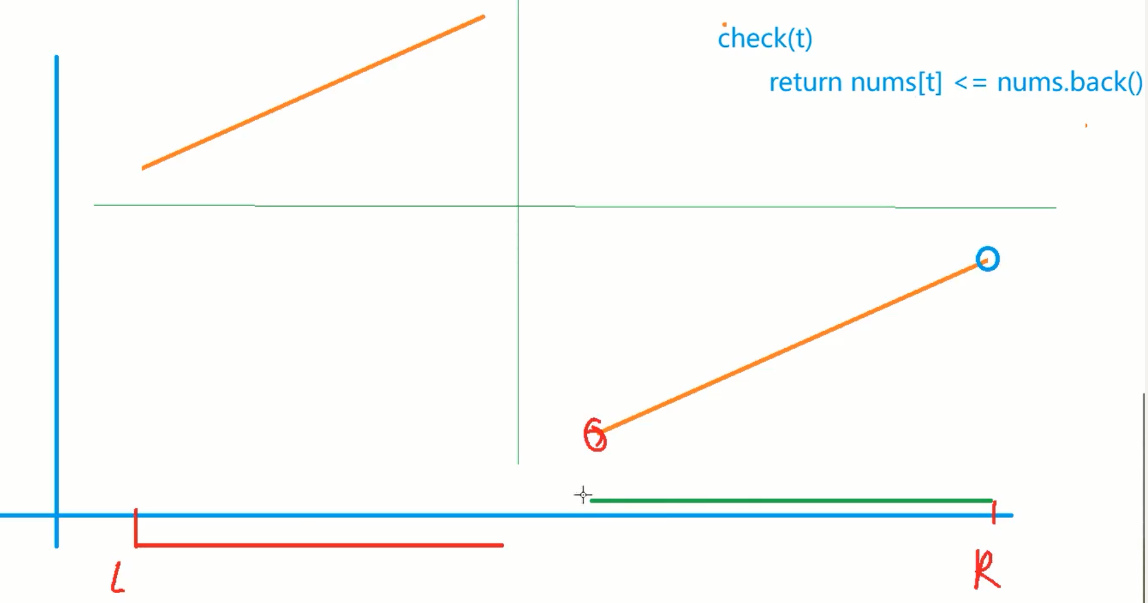
class Solution {
public:
int findMin(vector<int>& nums) {
int len = nums.size();
int l = 0, r = len - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] <= nums.back()) r = mid;
else l = mid + 1;
}
return nums[l];
}
};
Train of thought analysis:
This question is an advanced version of the previous question. We can find the minimum value of the rotation array through binary search according to the idea of the previous question. Then compare the last number of the array with the target number to narrow the range. Do another binary search.
class Solution {
public:
int search(vector<int>& nums, int target) {
int len = nums.size();
if (len == 0) return -1;
int l = 0, r = len - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (nums[mid] <= nums.back()) r = mid;
else l = mid + 1;
}
if (target <= nums.back()) r = len - 1;
else l = 0, r--;
while (l < r) {
int mid = (l + r) >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return nums[l] == target ? l : -1;
}
};
Train of thought analysis:
At a glance, you can see that it is 00001111. You can find the first 1 model and set a template.
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int l = 1, r = n;
while (l < r) {
int mid = l + (r - l >> 1);
if (isBadVersion(mid)) r = mid;
else l = mid + 1;
}
return l;
}
};
5. Summary
The above questions are just to brush the proficiency of binary search. The topic of [binary answer] will be summarized in the next sharing meeting. There may be more questions in the interview.