Refer to Google or tools for this article Official website documents Describes the use of or tools.
The description of packing problem is to put a set of items of given size into a container with fixed capacity. Generally, due to the capacity limitation of the container, it is impossible to put all items into the container. The goal of packing problem is to find a packing method with maximum value or minimum total cost under the restriction. According to our specific objectives, the packing problem can be divided into two categories:
- For knapsack problem, the number of containers is fixed, each container has its own maximum capacity, and the objects to be allocated have their own value. Our goal is to maximize the total value of the objects in the container, and not require all objects to be loaded;
- Bin packing problem, the container capacity is the same, but the quantity is not fixed, our goal is to use the least container to store all objects.
Or tools provides a special interface for a typical single knapsack problem. For more general multi knapsack problems and bin packing problems, a general integer programming interface is needed to calculate. In this article, I will use or tools to model single knapsack problem, multi knapsack problem and bin packing problem with reference to the official tutorial demonstration.
One knapsack problem
If there is only one knapsack in the knapsack problem, it is a single knapsack problem, which is also generally a 0-1 knapsack problem, because it can be described by the following equation:
Using the 0-1 variable XIX ﹣ IXI to indicate whether the third object is put into the backpack, VIV ﹣ IVI to indicate the value of object iii, wiw ﹣ iwi to indicate the weight of the object, and WWW to indicate the maximum load of the backpack, the whole problem can be expressed as follows:
maximize∑i=1nvixisubject to∑i=1nwixi≤Wxi∈{0,1}
\begin{aligned}
maximize\quad &\sum_{i=1}^n v_ix_i\\
subject\ to\quad& \sum_{i=1}^nw_ix_i\leq W \\
& x_i \in \{0,1\}
\end{aligned}
maximizesubject toi=1∑nvixii=1∑nwixi≤Wxi∈{0,1}
Of course, in real life, it is not only the weight, but also the volume that may limit the number of objects stored in the backpack. Therefore, the above definition should be a one-dimensional single backpack problem. If there is a multi-dimensional limit, the total amount of objects stored in each one-dimensional cannot exceed the limit value of the backpack.
We create a new. NET Core console application to customize the data of a single knapsack problem:
//values[i], the value of item i long[] values = { 360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147, 78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28, 87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276, 312 }; //weights[i,j], the weight of weights[i][j] long[,] weights = { { 7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0, 42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71, 3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13 } }; long[] capacities = { 850 };
Or tools provides a KnapsackSolver to deal with the single knapsack problem. We define the KnapsackSolver object and specify the branch definition algorithm
KnapsackSolver solver = new KnapsackSolver( KnapsackSolver.SolverType.KNAPSACK_MULTIDIMENSION_BRANCH_AND_BOUND_SOLVER, "KnapsackExample");
Then you can initialize the KnapsackSolver object and solve it
solver.Init(values, weights, capacities); long computedValue = solver.Solve();
The return value of the Solve() method is the final target value of the algorithm. If you want to know which objects are placed, you need to call the BestSolutionContains() method to view them.
Console.WriteLine("Optimal Value = " + computedValue); string selectItems = $"Selected item indexs : "; for (int i = 0; i < values.Length; i++) { if (solver.BestSolutionContains(i)) { selectItems += $"{i}({values[i]}), "; } } Console.WriteLine(selectItems);
Complete procedure
using System; using Google.OrTools.Algorithms; namespace SingleKnapsackProblem { class Program { static void Main(string[] args) { //Create a knapsack solver, use Branch And Bound algorithm KnapsackSolver solver = new KnapsackSolver( KnapsackSolver.SolverType.KNAPSACK_MULTIDIMENSION_BRANCH_AND_BOUND_SOLVER, "KnapsackExample"); //values[i], the value of item i long[] values = { 360, 83, 59, 130, 431, 67, 230, 52, 93, 125, 670, 892, 600, 38, 48, 147, 78, 256, 63, 17, 120, 164, 432, 35, 92, 110, 22, 42, 50, 323, 514, 28, 87, 73, 78, 15, 26, 78, 210, 36, 85, 189, 274, 43, 33, 10, 19, 389, 276, 312 }; //weights[i,j], the weight of weights[i][j] long[,] weights = { { 7, 0, 30, 22, 80, 94, 11, 81, 70, 64, 59, 18, 0, 36, 3, 8, 15, 42, 9, 0, 42, 47, 52, 32, 26, 48, 55, 6, 29, 84, 2, 4, 18, 56, 7, 29, 93, 44, 71, 3, 86, 66, 31, 65, 0, 79, 20, 65, 52, 13 } }; long[] capacities = { 850 }; solver.Init(values, weights, capacities); long computedValue = solver.Solve(); Console.WriteLine("Optimal Value = " + computedValue); string selectItems = $"Selected item indexs : "; for (int i = 0; i < values.Length; i++) { if (solver.BestSolutionContains(i)) { selectItems += $"{i}({values[i]}), "; } } Console.WriteLine(selectItems); } } }
2 multi knapsack problem
To extend a single knapsack to multiple knapsacks is a multi knapsack problem. For a multi knapsack problem, we can use the following definition method:
N n n objects and m m m knapsacks (m ≤ nm\leq nm ≤ n) are given and defined as follows (still single dimension):
vj: value of object j wj: weight of object j ci: capacity of the ith Backpack
\begin{aligned}
&V_j: the value of object J\
&W_j: weight of object J\
&C_i: capacity of the ith Backpack\
\end{aligned}
vj: value of object j wj: weight of object j ci: capacity of the ith Backpack
To maximize the total value of items placed without exceeding the capacity limit of each backpack, namely:
maximize∑i=1m∑j=1nvjxijsubject to∑j=1nwjxij≤ci,i∈M={1,...m}∑i=1mxij≤1,j∈N={1,...n}xij∈{0,1}
\begin{aligned}
maximize\quad &\sum_{i=1}^m\sum_{j=1}^n v_jx_{ij}\\
subject\ to\quad& \sum_{j=1}^nw_jx_{ij}\leq c_i, i\in M=\{1,...m\} \\
& \sum_{i=1}^mx_{ij}\leq 1, j\in N=\{1,...n\} \\
& x_{ij} \in \{0,1\}
\end{aligned}
maximizesubject toi=1∑mj=1∑nvjxijj=1∑nwjxij≤ci,i∈M={1,...m}i=1∑mxij≤1,j∈N={1,...n}xij∈{0,1}
Where xijx {ij} Xij is a 0-1 variable indicating whether the object jjj is assigned to knapsack iii.
For the multi knapsack problem, or tools does not provide a direct interface, but from its modeling equation, it is a typical integer programming problem, so we can use the integer programming interface of or tools for modeling and calculation.
Let's first customize the data source of a problem. Suppose there are 15 objects and 5 backpacks, and the maximum load of each backpack is 100
class DataModel { public double[] Weights = {48, 30, 42, 36, 36, 48, 42, 42, 36, 24, 30, 30, 42, 36, 36}; public double[] Values = {10, 30, 25, 50, 35, 30, 15, 40, 30, 35, 45, 10, 20, 30, 25}; public double[] BinCapacities = { 100, 100, 100, 100, 100 }; private int numItems; public int NumItems { get { numItems = Weights.Length; return numItems; } set { numItems = value; } } public int NumBins = 5; }
Create a new integer programming solution object, where the internal connection CBC solver is specified
// Create the linear solver with the CBC backend. Solver solver = Solver.CreateSolver("SimpleMipProgram", "CBC_MIXED_INTEGER_PROGRAMMING");
Then define the solving variables, i.e. I × ji\times ji × j 0-1 variables
// Create variables, x[i][j]=1 means item i is packed in bin j Variable[,] x = new Variable[data.NumItems,data.NumBins]; for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i,j] = solver.MakeIntVar(0, 1, String.Format("x_{0}_{1}", i, j)); } }
Then there are two constraints: one is that one object can only be allocated to one knapsack at most; the other is that the weight of objects in each knapsack will not exceed the limit
//Item i can't be packed in more than one bins for (int i = 0; i < data.NumItems; ++i) { LinearExpr sum=new LinearExpr(); for (int j = 0; j < data.NumBins; ++j) { sum += x[i,j]; } solver.Add(sum <= 1.0); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { LinearExpr Weight=new LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { Weight += data.Weights[i] * x[i,j]; } solver.Add(Weight <= data.BinCapacities[j]); }
At last, we can define the goal and solve it
//Objective LinearExpr totalValue=new LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { for (int j = 0; j < data.NumBins; ++j) { totalValue += data.Values[i] * x[i,j]; } } solver.Maximize(totalValue); //Solve it Solver.ResultStatus resultStatus = solver.Solve();
Complete code
using System; using Google.OrTools.LinearSolver; namespace MultipleKnapsackProblem { class Program { class DataModel { public double[] Weights = {48, 30, 42, 36, 36, 48, 42, 42, 36, 24, 30, 30, 42, 36, 36}; public double[] Values = {10, 30, 25, 50, 35, 30, 15, 40, 30, 35, 45, 10, 20, 30, 25}; public double[] BinCapacities = { 100, 100, 100, 100, 100 }; private int numItems; public int NumItems { get { numItems = Weights.Length; return numItems; } set { numItems = value; } } public int NumBins = 5; } static void Main(string[] args) { DataModel data = new DataModel(); // Create the linear solver with the CBC backend. Solver solver = Solver.CreateSolver("SimpleMipProgram", "CBC_MIXED_INTEGER_PROGRAMMING"); // Create variables, x[i][j]=1 means item i is packed in bin j Variable[,] x = new Variable[data.NumItems,data.NumBins]; for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i,j] = solver.MakeIntVar(0, 1, String.Format("x_{0}_{1}", i, j)); } } //Item i can't be packed in more than one bins for (int i = 0; i < data.NumItems; ++i) { LinearExpr sum=new LinearExpr(); for (int j = 0; j < data.NumBins; ++j) { sum += x[i,j]; } solver.Add(sum <= 1.0); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { LinearExpr Weight=new LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { Weight += data.Weights[i] * x[i,j]; } solver.Add(Weight <= data.BinCapacities[j]); } //Objective LinearExpr totalValue=new LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { for (int j = 0; j < data.NumBins; ++j) { totalValue += data.Values[i] * x[i,j]; } } solver.Maximize(totalValue); //Solve it Solver.ResultStatus resultStatus = solver.Solve(); // Check that the problem has an optimal solution. if (resultStatus != Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Total packed value: " + solver.Objective().Value()); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; double BinValue = 0; Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (x[i,j].SolutionValue() == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i] + " values: " + data.Values[i]); BinWeight += data.Weights[i]; BinValue += data.Values[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); Console.WriteLine("Packed bin value: " + BinValue); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); } } }
3 bin packing problem
3.1 using integer solver
Different from knapsack problem, bin packing problem is defined from the perspective of container optimization. Instead of considering the value of placing objects, we want to use the least number of containers to hold all objects. Bin packing problem is more general than knapsack problem, which is often encountered in the field of logistics in life, such as using the least transport vehicles to deliver express delivery to minimize the cost. Bin packing problem can also be expressed by integer programming model:
Give enough bins (bin) s1s S1, S2S S2 , Sm, s ﹣ m, Sm, each box has the same capacity CCC; nnn items need to be packed, each item has its own weight w1w ﹣ 1w1, W2W ﹣ 2w2 We want to pack everything in the least number of boxes:
minimizeB=∑i=1nyisubject to∑j=1nwjxij≤Cyi,i∈M={1,...m}∑i=1mxij=1,j∈N={1,...n}xij∈{0,1}yi∈{0,1}
\begin{aligned}
minimize\quad& B=\sum_{i=1}^ny_i\\
subject\ to\quad& \sum_{j=1}^nw_jx_{ij}\leq Cy_i, i\in M=\{1,...m\} \\
& \sum_{i=1}^mx_{ij}= 1, j\in N=\{1,...n\} \\
& x_{ij} \in \{0,1\} \\
& y_{i}\in \{0,1\}
\end{aligned}
minimizesubject toB=i=1∑nyij=1∑nwjxij≤Cyi,i∈M={1,...m}i=1∑mxij=1,j∈N={1,...n}xij∈{0,1}yi∈{0,1}
Where yiy ﹣ iyi indicates whether the case iii is used, and xijx {ij} Xij indicates whether the object jjj is loaded into the case iii.
We use the integer programming solving interface of or tools to deal with this problem. First, customize the data. Here I use a class to encapsulate the problem data. numItems represents the number of items to be packed, binCapacity represents the capacity of each box, numBins represents the number of boxes available for use. If it is empty, it is replaced by the number of items. The weight of each item is randomly set to a value less than the capacity.
class DataModel { public DataModel(int numItems, double binCapacity, int? numBins=null) { this.numItems = numItems; this.binCapacity = binCapacity; if (numBins.HasValue) { this.numBins = numBins.Value; } else { this.numBins = numItems; } weights = new double[numItems]; for(int i=0;i<numItems;i++) { weights[i] = new Random(Guid.NewGuid().GetHashCode()).Next(1, Convert.ToInt32(binCapacity)); } } private double[] weights; public double[] Weights { get { return weights; } set { weights = value; } } private double binCapacity; public double BinCapacity { get { return binCapacity; } set { binCapacity = value; } } private int numItems; public int NumItems { get { return numItems; } set { numItems = value; } } private int numBins; public int NumBins { get { return numBins; } set { numBins = value; } } }
Create a CBC integer solver object and define a solution target
// Create the linear solver with the CBC backend. GoogleLinearSolver.Solver solver = GoogleLinearSolver.Solver.CreateSolver("SimpleMipProgram", "CBC_MIXED_INTEGER_PROGRAMMING"); // Create variables, x[i][j]=1 means item i is packed in bin j GoogleLinearSolver.Variable[,] x = new GoogleLinearSolver.Variable[data.NumItems, data.NumBins]; for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i, j] = solver.MakeIntVar(0, 1, String.Format("x_{0}_{1}", i, j)); } } //y[j]=1 means bin j is used GoogleLinearSolver.Variable[] y = new GoogleLinearSolver.Variable[data.NumBins]; for (int j = 0; j < data.NumBins; j++) { y[j] = solver.MakeIntVar(0, 1, string.Format("y_{0}", j)); }
Define constraints. Constraint 1, each object must be allocated to a certain box; constraint 2, the allocated object in each box cannot exceed the capacity
//Each item must be in exactly one bin. for (int i = 0; i < data.NumItems; ++i) { GoogleLinearSolver.LinearExpr sum = new GoogleLinearSolver.LinearExpr(); for (int j = 0; j < data.NumBins; ++j) { sum += x[i, j]; } solver.Add(sum == 1.0); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { GoogleLinearSolver.LinearExpr Weight = new GoogleLinearSolver.LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { Weight += data.Weights[i] * x[i, j]; } solver.Add(Weight <= data.BinCapacity * y[j]); }
Finally, define the goal and solve it
//Objective GoogleLinearSolver.LinearExpr numBinsUsed = new GoogleLinearSolver.LinearExpr(); for (int j = 0; j < data.NumItems; ++j) { numBinsUsed += y[j]; } solver.Minimize(numBinsUsed); System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); GoogleLinearSolver.Solver.ResultStatus resultStatus = solver.Solve(); stopwatch.Stop(); Console.WriteLine($"Calculate time: {stopwatch.ElapsedMilliseconds / 1000} s , {stopwatch.ElapsedMilliseconds} ms"); // Check that the problem has an optimal solution. if (resultStatus != GoogleLinearSolver.Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Number of bins used: " + solver.Objective().Value()); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; if (y[j].SolutionValue() == 1) { Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (x[i, j].SolutionValue() == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i]); BinWeight += data.Weights[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); }
The following is the result of calculating 10 objects with a box capacity of 100
3.2 using SAT solver
On the other hand, we can also regard the Bin Packing problem as a constraint satisfaction model. The solution variables and constraint relations are consistent with those in the above integer programming expression. We can use the SAP solver of or tools to calculate this problem. Because there are essential differences in the algorithms used, we can test the efficiency differences between the two solutions
The following is the complete program code. The SolveItWithMixedIntegerSolver method is to use integer programming to solve the interface calculation, while SolveItWithSATSolver uses SAP to solve the interface calculation.
using System; using System.Collections.Generic; using GoogleLinearSolver=Google.OrTools.LinearSolver; using GoogleSat = Google.OrTools.Sat; namespace BinPackingProblem { class Program { class DataModel { public DataModel(int numItems, double binCapacity, int? numBins=null) { this.numItems = numItems; this.binCapacity = binCapacity; if (numBins.HasValue) { this.numBins = numBins.Value; } else { this.numBins = numItems; } weights = new double[numItems]; for(int i=0;i<numItems;i++) { weights[i] = new Random(Guid.NewGuid().GetHashCode()).Next(1, Convert.ToInt32(binCapacity)); } } private double[] weights; public double[] Weights { get { return weights; } set { weights = value; } } //public double[] Weights = { 48, 30, 19, 36, 36, 27, 42, 42, 36, 24, 30 }; private double binCapacity; public double BinCapacity { get { return binCapacity; } set { binCapacity = value; } } private int numItems; public int NumItems { get { return numItems; } set { numItems = value; } } private int numBins; public int NumBins { get { return numBins; } set { numBins = value; } } } static void Main(string[] args) { DataModel data = new DataModel(10,100,10); Console.WriteLine("###################Use Mixed Integer Solver##########################"); SolveItWithMixedIntegerSolver(data); Console.WriteLine("###################Use SAT Solver##########################"); SolveItWithSATSolver(data); } static void SolveItWithMixedIntegerSolver(DataModel data) { // Create the linear solver with the CBC backend. GoogleLinearSolver.Solver solver = GoogleLinearSolver.Solver.CreateSolver("SimpleMipProgram", "CBC_MIXED_INTEGER_PROGRAMMING"); // Create variables, x[i][j]=1 means item i is packed in bin j GoogleLinearSolver.Variable[,] x = new GoogleLinearSolver.Variable[data.NumItems, data.NumBins]; for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i, j] = solver.MakeIntVar(0, 1, String.Format("x_{0}_{1}", i, j)); } } //y[j]=1 means bin j is used GoogleLinearSolver.Variable[] y = new GoogleLinearSolver.Variable[data.NumBins]; for (int j = 0; j < data.NumBins; j++) { y[j] = solver.MakeIntVar(0, 1, string.Format("y_{0}", j)); } //Each item must be in exactly one bin. for (int i = 0; i < data.NumItems; ++i) { GoogleLinearSolver.LinearExpr sum = new GoogleLinearSolver.LinearExpr(); for (int j = 0; j < data.NumBins; ++j) { sum += x[i, j]; } solver.Add(sum == 1.0); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { GoogleLinearSolver.LinearExpr Weight = new GoogleLinearSolver.LinearExpr(); for (int i = 0; i < data.NumItems; ++i) { Weight += data.Weights[i] * x[i, j]; } solver.Add(Weight <= data.BinCapacity * y[j]); } //Objective GoogleLinearSolver.LinearExpr numBinsUsed = new GoogleLinearSolver.LinearExpr(); for (int j = 0; j < data.NumBins; ++j) { numBinsUsed += y[j]; } solver.Minimize(numBinsUsed); System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); GoogleLinearSolver.Solver.ResultStatus resultStatus = solver.Solve(); stopwatch.Stop(); Console.WriteLine($"Calculate time: {stopwatch.ElapsedMilliseconds / 1000} s , {stopwatch.ElapsedMilliseconds} ms"); // Check that the problem has an optimal solution. if (resultStatus != GoogleLinearSolver.Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Number of bins used: " + solver.Objective().Value()); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; if (y[j].SolutionValue() == 1) { Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (x[i, j].SolutionValue() == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i]); BinWeight += data.Weights[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); } } static void SolveItWithSATSolver(DataModel data) { GoogleSat.CpModel cpModel = new GoogleSat.CpModel(); GoogleSat.IntVar[,] x = new GoogleSat.IntVar[data.NumItems, data.NumBins]; // Create variables, x[i][j]=1 means item i is packed in bin j for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i, j] = cpModel.NewBoolVar(String.Format("x_{0}_{1}", i, j)); } } //y[j]=1 means bin j is used GoogleSat.IntVar[] y = new GoogleSat.IntVar[data.NumBins]; for (int j = 0; j < data.NumBins; j++) { y[j] = cpModel.NewBoolVar(string.Format("y_{0}", j)); } //Each item must be in exactly one bin. for (int i = 0; i < data.NumItems; ++i) { List<GoogleSat.IntVar> items = new List<GoogleSat.IntVar>(); for (int j = 0; j < data.NumBins; ++j) { items.Add(x[i, j]); } cpModel.Add(GoogleSat.LinearExpr.Sum(items) == 1); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { List<GoogleSat.IntVar> itemWeights = new List<GoogleSat.IntVar>(); for (int i = 0; i < data.NumItems; ++i) { var currentWeight = cpModel.NewIntVar(0, Convert.ToInt32(data.Weights[i]), ""); cpModel.Add(currentWeight == Convert.ToInt32(data.Weights[i]) * x[i, j]); itemWeights.Add(currentWeight); } var currentMaxCapacity = cpModel.NewIntVar(0, Convert.ToInt32(data.BinCapacity), ""); cpModel.Add(currentMaxCapacity == Convert.ToInt32(data.BinCapacity) * y[j]); cpModel.Add(GoogleSat.LinearExpr.Sum(itemWeights) <= currentMaxCapacity); } //Objective List<GoogleSat.IntVar> numBinsUsed = new List<GoogleSat.IntVar>(); for (int j = 0; j < data.NumBins; ++j) { numBinsUsed.Add(y[j]); } cpModel.Minimize(GoogleSat.LinearExpr.Sum(numBinsUsed)); System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); var solver = new GoogleSat.CpSolver(); var resultStatus = solver.Solve(cpModel); stopwatch.Stop(); Console.WriteLine($"Calculate time: {stopwatch.ElapsedMilliseconds / 1000} s , {stopwatch.ElapsedMilliseconds} ms"); // Check that the problem has an optimal solution. if (resultStatus != GoogleSat.CpSolverStatus.Optimal || resultStatus == GoogleSat.CpSolverStatus.Feasible) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Number of bins used: " + solver.ObjectiveValue); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; if (solver.Value(y[j]) == 1) { Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (solver.Value(x[i, j]) == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i]); BinWeight += data.Weights[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); } } } } for (int i = 0; i < data.NumItems; ++i) { Weight += data.Weights[i] * x[i, j]; } solver.Add(Weight <= data.BinCapacity * y[j]); } //Objective GoogleLinearSolver.LinearExpr numBinsUsed = new GoogleLinearSolver.LinearExpr(); for (int j = 0; j < data.NumItems; ++j) { numBinsUsed += y[j]; } solver.Minimize(numBinsUsed); System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); GoogleLinearSolver.Solver.ResultStatus resultStatus = solver.Solve(); stopwatch.Stop(); Console.WriteLine($"Calculate time: {stopwatch.ElapsedMilliseconds / 1000} s , {stopwatch.ElapsedMilliseconds} ms"); // Check that the problem has an optimal solution. if (resultStatus != GoogleLinearSolver.Solver.ResultStatus.OPTIMAL) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Number of bins used: " + solver.Objective().Value()); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; if (y[j].SolutionValue() == 1) { Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (x[i, j].SolutionValue() == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i]); BinWeight += data.Weights[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); } } static void SolveItWithSATSolver(DataModel data) { GoogleSat.CpModel cpModel = new GoogleSat.CpModel(); GoogleSat.IntVar[,] x = new GoogleSat.IntVar[data.NumItems, data.NumBins]; // Create variables, x[i][j]=1 means item i is packed in bin j for (int i = 0; i < data.NumItems; i++) { for (int j = 0; j < data.NumBins; j++) { x[i, j] = cpModel.NewBoolVar(String.Format("x_{0}_{1}", i, j)); } } //y[j]=1 means bin j is used GoogleSat.IntVar[] y = new GoogleSat.IntVar[data.NumBins]; for (int j = 0; j < data.NumBins; j++) { y[j] = cpModel.NewBoolVar(string.Format("y_{0}", j)); } //Each item must be in exactly one bin. for (int i = 0; i < data.NumItems; ++i) { List<GoogleSat.IntVar> items = new List<GoogleSat.IntVar>(); for (int j = 0; j < data.NumBins; ++j) { items.Add(x[i, j]); } cpModel.Add(GoogleSat.LinearExpr.Sum(items) == 1); } //The amount packed in each bin cannot exceed its capacity for (int j = 0; j < data.NumBins; ++j) { List<GoogleSat.IntVar> itemWeights = new List<GoogleSat.IntVar>(); for (int i = 0; i < data.NumItems; ++i) { var currentWeight = cpModel.NewIntVar(0, Convert.ToInt32(data.Weights[i]), ""); cpModel.Add(currentWeight == Convert.ToInt32(data.Weights[i]) * x[i, j]); itemWeights.Add(currentWeight); } var currentMaxCapacity = cpModel.NewIntVar(0, Convert.ToInt32(data.BinCapacity), ""); cpModel.Add(currentMaxCapacity == Convert.ToInt32(data.BinCapacity) * y[j]); cpModel.Add(GoogleSat.LinearExpr.Sum(itemWeights) <= currentMaxCapacity); } //Objective List<GoogleSat.IntVar> numBinsUsed = new List<GoogleSat.IntVar>(); for (int j = 0; j < data.NumItems; ++j) { numBinsUsed.Add(y[j]); } cpModel.Minimize(GoogleSat.LinearExpr.Sum(numBinsUsed)); System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); var solver = new GoogleSat.CpSolver(); var resultStatus = solver.Solve(cpModel); stopwatch.Stop(); Console.WriteLine($"Calculate time: {stopwatch.ElapsedMilliseconds / 1000} s , {stopwatch.ElapsedMilliseconds} ms"); // Check that the problem has an optimal solution. if (resultStatus != GoogleSat.CpSolverStatus.Optimal || resultStatus == GoogleSat.CpSolverStatus.Feasible) { Console.WriteLine("The problem does not have an optimal solution!"); return; } Console.WriteLine("Number of bins used: " + solver.ObjectiveValue); double TotalWeight = 0; for (int j = 0; j < data.NumBins; ++j) { double BinWeight = 0; if (solver.Value(y[j]) == 1) { Console.WriteLine("Bin " + j); for (int i = 0; i < data.NumItems; ++i) { if (solver.Value(x[i, j]) == 1) { Console.WriteLine("Item " + i + " weight: " + data.Weights[i]); BinWeight += data.Weights[i]; } } Console.WriteLine("Packed bin weight: " + BinWeight); TotalWeight += BinWeight; } Console.WriteLine("Total packed weight: " + TotalWeight); } } } }
When the number of objects is 10, the two solutions take about 24ms and 127ms, respectively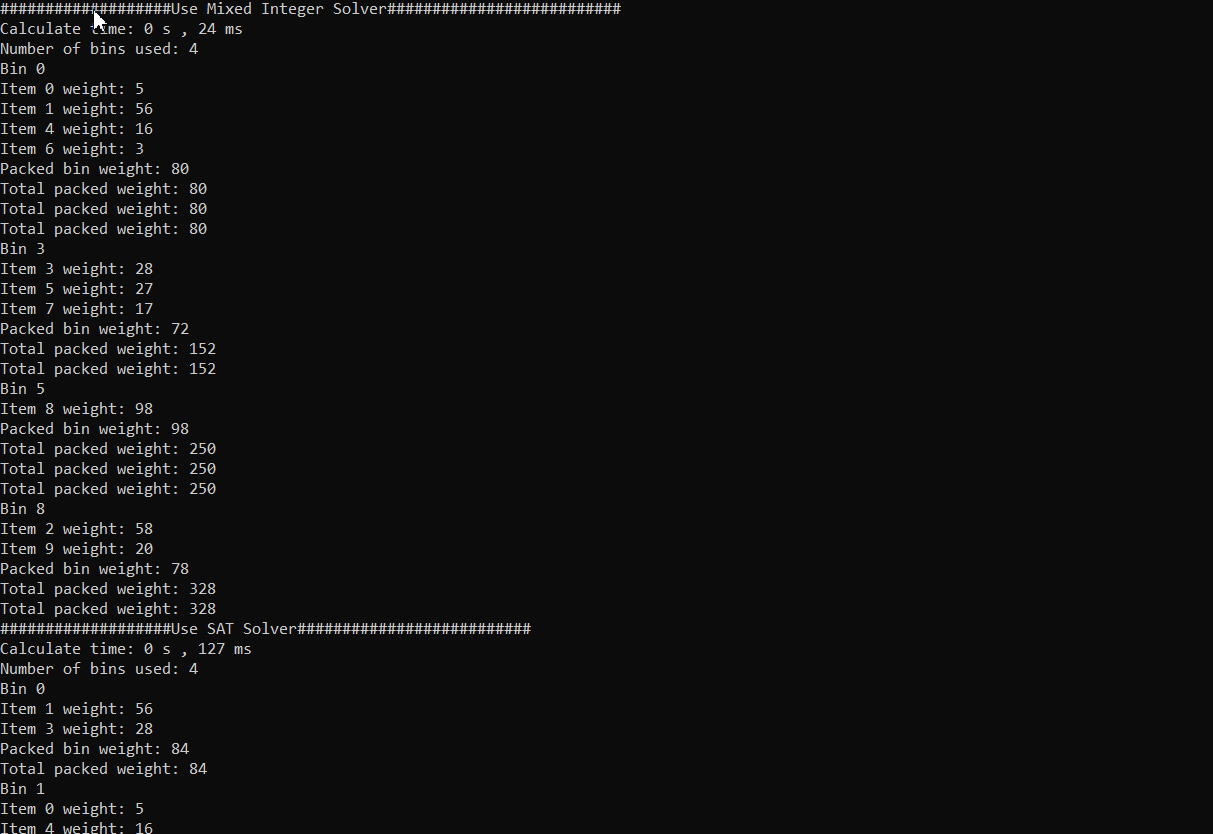
When the number of objects is set to 15, it takes 100ms to use the integer solver, while it takes up to 4 seconds to use the SAT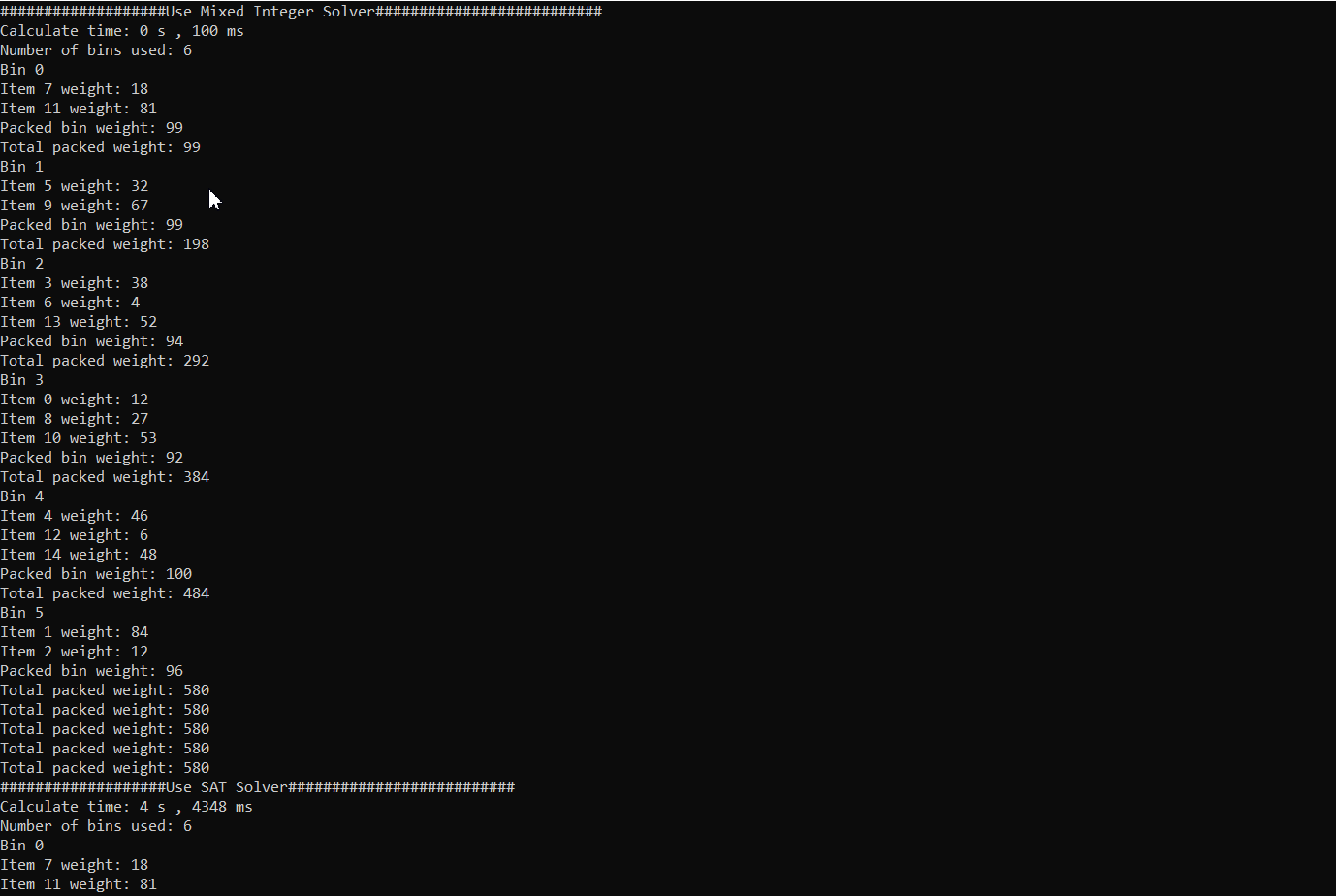
It can be seen that for the standard Bin Packing problem, the integer programming model and the integer programming algorithm (such as branch definition) are more suitable. This is also in line with the general idea of solving optimization problems. Try to build the model in the direction of linear programming model, unless it is a constraint satisfaction or combination optimization problem that cannot be expressed by a unified expression.

