• insert

  • Assign a value to the new node first

    	New->pre = My;
    	New->next = My->next;
    

  • Modify the front and back nodes

    	My->next->pre = New;
    	My->next = New;
    

  New - > next = my - > next; and my - > next - > pre = new; positions can be changed.

  This changes to the front node first and then to next.

• delete

  	if ( NULL != My->next )
  	{
  	    temp = My->next;
  	    My->next = My->next->next;
  		temp->next = NULL;
  		delete temp;//free(temp)
  	}
  

• KMP

  It is mainly to optimize the search of substring and improve the substring substr Work efficiency and auxiliary function in matching.

  In the algorithm next Refer to:stay i If a mismatch is found at, the next[i]Start the control.

  next[i]Corresponding value representation,stay substr+i-next[i]There are next[i]One and substr Same prefix.

  i The value of is determined by the calculation of the preceding character.

  

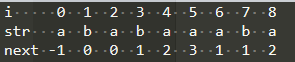
  For a substring if shown. For any one next The value of is greater than 0, indicating that there is a period. Or the front is the same.

  i	str	introduction	value
  0	a	front,Not the same, error	-1
  1	b	i<2	0
  2	a	a!=b	0
  3	b	a==a	1
  4	a	ab==ab	2
  5	a	aba==aba	3
  6	a	abab!=abaa,aba!=baa,ab!=aa,a==a	1
  7	b	ab!=aa,a==a	1
  8	a	ab==ab	2
  9	x	aba==aba,because i==len,So there's no such value. value Indicates that there is n Identical	3

• KMP optimized version

  Remove the redundancy on the basis of the previous.

  

  Transformation logic

  If there are repetitions, it can be understood that f (x) = f (X-R), and R is the period.

  Values can be divided into two categories, - 1 or non-1

  -1 means that if it is found that it is different at present, the previous one can be ignored. The subscripts of str and substr can be + + at the same time, because there is no substring with a cycle length of currentdex in the substring.

  Non-1 means that there must be n identical ones in front, but they start to be different in my (currentIndex)

  For example, the value of 5 below is 3, indicating that there are three identical, but they are not the same here. The first one is in the place with subscript 3. The same is aba==aba, but there is abab!=abaa.

  For 0, it is because j==-1,next is the former relationship, and j==-1 means that both start again.

  j==0 compared to - 1, because there is no former, and the current loop does not form is not equal. In the starting state.

  For i==1, without the former, it is a step forward together. Judging the current a!=b, there will be, next[1]==0. If str[1]==a, then b==-1. Because for a certain period of periodic function, there is the same, you can move forward n times the period to form a graphic overlap.

  i	next[i]	j	introduction	next[++j]	next[++i]
  0	-1	-1	j==-1,a!=b	j==0,value==-1	i==1,value==0
  1	0	0	a!=b, backtracking	j==0,value==-1
  1	0	-1	j==-1,a==a	j==0,value==-1	i==2,value==-1
  2	-1	0	a==a,b==b	j==1,value==0	i==3,value=0
  3	0	1	b==b,a==a	j==2,value==-1	i==4,value==-1
  4	-1	2	a==a,b!=a	j==3,value==0	i==5,value=j=3
  5	3	3	b!=a, backtracking	j==0,value==-1
  5	3	0	a==a,b!=a	j==1,value==0	i==6,value=j=1
  6	1	1	b!=a, backtracking	j==0,value==-1
  6	1	0	a==a,b!=a	j==1,value==0	i==7,value==0
  7	0	1	b==b,a==a	j==2,value==-1	i==8,value==-1

• source code

  	#include<stdio.h>
  	#include<string.h>
  
  	void get_KMP_Next(const char * src,int len,int *next)
  	{
  		int i,j;
  		next[0] = j = -1;
  		i = 0;
  		while( i < len )
  		{
  			if( j == -1 || src[i] == src[j] )
  			{
  				i++;
  				j++;
  				next[i] = j ;
  				//Indicates that if the location of i does not match, the starting matching address needs to be moved to the location of j.
  			}
  			else
  			{
  				j = next[j];
  			}
  		}
  	}
  
  	void get_KMP_NextValue(const char * src,int len,int *next)
  	{
  		int i,j;
  		next[0] = j = -1;
  		i = 0;
  		while( i < len )
  		{
  			if( j == -1 || src[i] == src[j] )
  			{
  				i++;
  				j++;
  				if ( src[i] != src[j] )
  				{
  					//For inequality, the repetition is stopped.
  					next[i] = j;
  				}
  				else
  				{
  					next[i] = next[j];
  					//Continuous equality indicates that a certain substring has a high repetition rate.
  					// abcabcabcabc or aaaaaa, the repetition rate is very high
  					// AAAA ABAB ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCD defg is all.
  					//For this kind of high repetition rate
  					//For AAAA type A, only the first one is needed.
  					//For ababa periodic strings, use j's next.
  					//It can be summed up as a mathematical periodic function, such as tan(x), with high repeatability.
  				}
  			}
  			else
  			{
  				j = next[j];
  			}
  		}
  	}
  
  	void (*getNext)(const char*,int,int*) = get_KMP_NextValue;
  	//To switch between the improved version and the non improved version, you only need to copy the corresponding method name.
  	int searchSub(const char * src,int srclen ,const char* sub,int sublen)
  	{
  		int next[255]={0},i,j;
  		getNext(sub,sublen,next);
  		for(i = 0 ; i < sublen ; i++ )
  		{
  			printf(i<sublen-1?"%d ":"%d\n",next[i]);
  		}
  		j = i = 0 ;
  		while( i < srclen && j < sublen )
  		{
  			if( j == -1 || src[i] == sub[j] )
  			{
  				i++;
  				j++;
  			}
  			else
  			{
  				j = next[j];
  			}
  		}
  		if ( j == sublen )
  		{
  			return i - sublen;
  		}
  		else
  		{
  			return -1;
  		}
  	}
  
  	void testSub()
  	{
  		char src[] = "abcdabcdexabcde";
  		char sub[] = "abcdex";
  		int srclen = strlen(src),sublen=strlen(sub);
  		int ret = searchSub(src,srclen,sub,sublen);
  		if ( ret != -1 )
  		{
  			printf("%s\n",src + ret);
  		}
  		else
  		{
  			printf("error\n");
  		}
  	}
  
  	void printNext()
  	{
  		char sub[] = "ababaaaba";
  		int next[255]={0},sublen=strlen(sub),i;
  		getNext(sub,sublen,next);
  		printf("i   ");
  		for( i = 0 ; i < sublen ; i++ )
  		{
  			printf("%3d",i);
  		}
  		printf("\nstr ");
  		for( i = 0 ; i < sublen ; i++ )
  		{
  			printf("  %c",sub[i]);
  		}
  		printf("\nnext");
  		for( i = 0 ; i < sublen ; i++ )
  		{
  			printf("%3d",next[i]);
  		}
  		printf("\n");
  	}
  
  	int main()
  	{
  		printNext();
  		return 0;
  	}
  

Clue binary tree