Breadth first search

Compared with deep search, wide search is much faster than deep search in a certain situation. For example, to find the shortest path of maze, wide search is better than deep search. This is not a question of whether to use recursion, but how fast it is at the algorithm level.
For example:
Define a 2D array:
int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

It represents a maze, in which 1 represents the wall, 0 represents the path that can be walked, can only walk horizontally or vertically, can't walk obliquely, and requires programming to find the shortest path from the upper left corner to the lower right corner.
Input
A 5 × 5 two-dimensional array represents a maze. Data guarantees a unique solution.
Output
The shortest path from the upper left corner to the lower right corner, in the format shown in the example.
Sample Input
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

This is a very basic search question, it is OK to use deep search, but if you choose to use deep search to write, it means that you need to go through all the situations, compare their sizes and choose again. And it's not easy to save the path. What you have to do is two steps: 1. Find the shortest path 2 and update the path value to the shortest path. It's very troublesome.
But it's not the same if you choose broad search. The priority of broad search is all roads. That is to say, when you reach the target point, the end is the shortest path. And unlike deep search, every path of broad search is saved in the queue, which facilitates our printing path

#include <stdio.h>
#include <stdlib.h>
struct note
{
    int x;
    int y;
    int s;
    int f;
};
int main()
{
    struct note que[50];
    int a[51][51]={0},book[51][51]={0},shu[50][2],w;
    int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
    int head,tail;
    int i,j,k,n,m,startx,starty,p,q,tx,ty,flag;

    for(i=1;i<=5;i++)
        for(j=1;j<=5;j++)
        scanf("%d",&a[i][j]);

    head=1;
    tail=1;
    que[tail].x=1;
    que[tail].y=1;
    que[tail].f=0;
    que[tail].s=0;
    tail++;
    book[1][1]=1;
    flag=0;
    while(head<tail)
    {
        for(k=0;k<=3;k++)
        {
            tx=que[head].x+next[k][0];
            ty=que[head].y+next[k][1];
            if(tx<1||tx>5||ty<1||ty>5)
                continue;
            if(a[tx][ty]==0&&book[tx][ty]==0)
            {
                book[tx][ty]=1;
                que[tail].x=tx;
                que[tail].y=ty;
                que[tail].f=head; //This is where the path is recorded
                que[tail].s=que[head].s+1;
                tail++;
            }
            if(tx==5&&ty==5)
            {
                flag=1;
                break;
            }
        }
        if(flag==1)
            break;
        head++;
    }
    tail=tail-1;
    shu[0][0]=5;
    shu[0][1]=5;
    w=1;
    while(que[tail].f!=0)
    {
        shu[w][0]=que[que[tail].f].x;    //Use what you just saved to find the way out
        shu[w][1]=que[que[tail].f].y;
        que[tail].f=que[que[tail].f].f;
        w++;
    }
    for(i=w-1;i>=0;i--)
    {
        printf("(%d, %d)",shu[i][0]-1,shu[i][1]-1);
        printf("\n");
    }
    return 0;
}

Two points

The main idea of dichotomy:

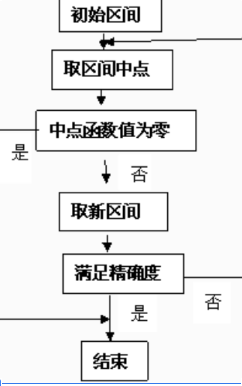
It is a simple but practical method, but when using dichotomy, we should pay attention to what is the end point of dichotomy and what is the parameter of dichotomy. In short, we need to know who we are. Like the following question, what we divide is not his x, but the obtained and y, so we need to write another function to calculate the sum of returns under different mid.

Now,given the equation 8x^4 + 7x^3 + 2x^2 + 3x + 6 == Y,can you find its solution between 0 and 100;
Now please try your lucky.
Input
The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has a real number Y (fabs(Y) <= 1e10);
Output
For each test case, you should just output one real number(accurate up to 4 decimal places),which is the solution of the equation,or "No solution!",if there is no solution for the equation between 0 and 100.
Sample Input
2
100
-4
Sample Output
1.6152
No solution!

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
double pan(double x);
double pan(double x)
{
    return 8*pow(x,4)+7*pow(x,3)+2*pow(x,2)+3*x+6;
}
void suan(double y)
{
     double mid;
     double shou,y1;
     y1=y;
     shou=0;
     while(1)
     {
         mid=(shou+y1)/2;
         if(pan(mid)>y)         //It's similar to finding zero. To find zero, we need to find one side is larger than zero and the other side is smaller than zero
         {
             y1=mid;
         }
         else if(pan(mid)<y)
         {
             shou=mid;
         }
         if(pan(mid)-y<0.000001&&pan(mid)-y>0)//Pay special attention to this step
         {
             printf("%0.4lf\n",mid);
             break;
         }
     }

}
int main()
{
    int t;
    double y;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lf",&y);
        if(y<pan(0)||y>pan(100))
        {
            printf("No solution!\n");
        }
        else
        {
            suan(y);
        }
    }
    return 0;
}