Width-first searches are primarily used for queues, a data structure that comes out after data is advanced
The main idea is to queue the data that is searched at each step so that the queue can ensure that the data of the same depth is linearly arranged in the continuous space of the queue, so that all data of the same depth (breadth first) can be processed in the same batch each time, so that the depth of the data you want to search can be found steadily
Here is an example:
(Title from: https://leetcode-cn.com/explore/learn/card/queue-stack/217/queue-and-bfs/873/)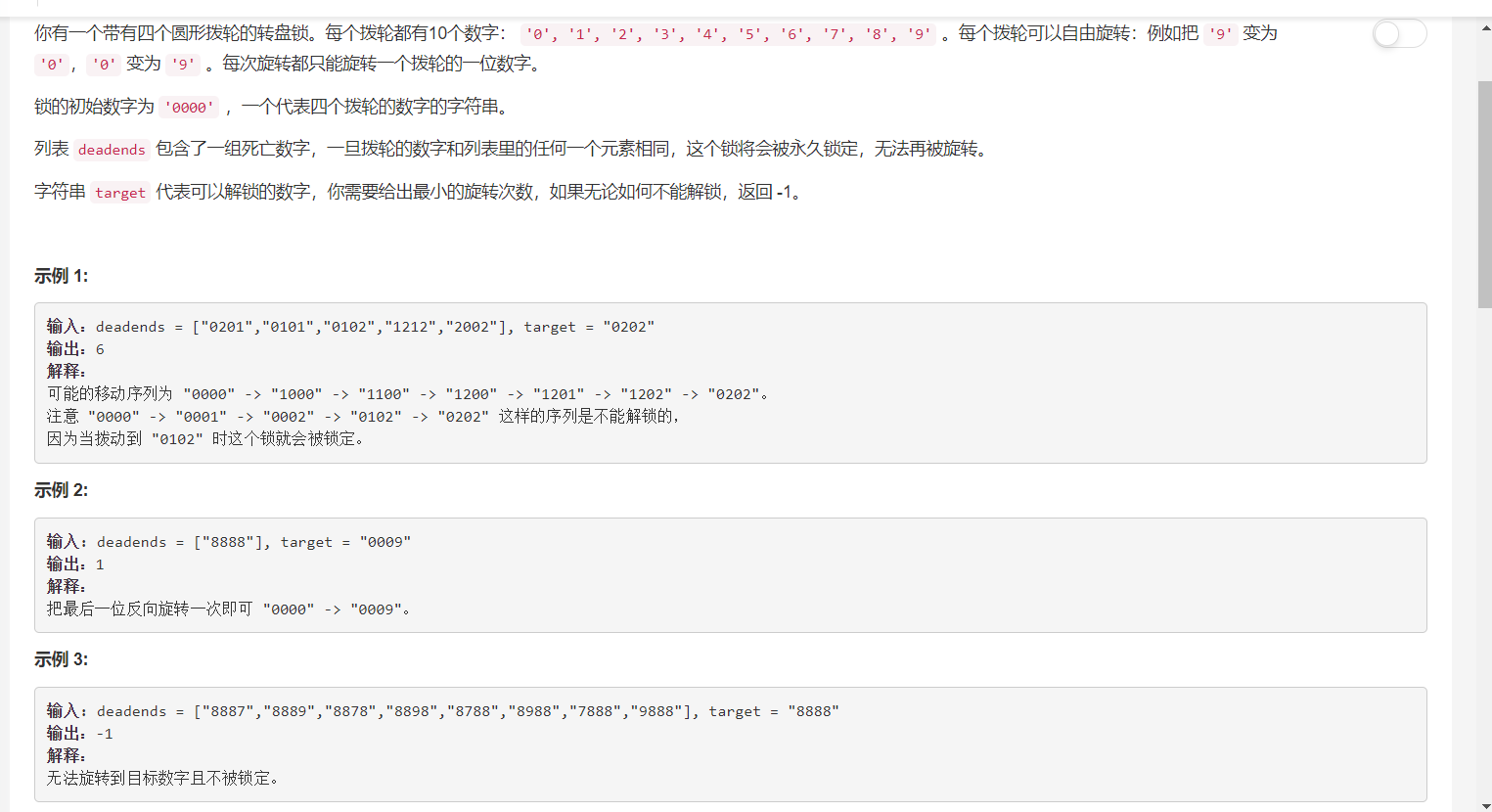

(Answer template given in title)

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        
    }
};

Given that this question can be solved with a breadth-first search
Given that direct manipulation strings are cumbersome and code readability decreases a lot, two inline functions are set

    inline string Add(string num,int index)
	{
		num[i] = (num[i] - 47) % 10 + 48;
		return num;
	}
	inline string Sub(string num,int index)
	{
		num[i] = (num[i] - 39) % 10 + 48;
		return num;
	}

This indirectly achieves the effect of dialing forward and backward passwords
We need a node queue < string > nodes to hold the results of each search when using breadth first search
Save all searched data with a collection set < string > user to prevent multiple entries of the searched data into the queue nodes from being repeatedly searched (for example, 0350 can be searched by depth 3 0340, 0330 by depth 4, 0330 by depth 5 0250, 0330 by depth 6, which results in depth 4 and depth 6 being searched when searchingThis may result in a dead cycle in SO 0330)
Notice also that there is a password deadends in the title that cannot be set. We can interpret it as having appeared in previous searches and not in future searches.So we can incorporate these deadends into the user.The starting code is as follows:

int openLock(vector<string>& deadends, string target) {
		string now = "0000";//Initial password
		set<string> used;
		queue<string> nodes;
		for (int i = 0; i != deadends.size(); i++)
			used.insert(deadends[i]);
		}

When the length of the queue is zero, we have traversed all the nodes, which can be used as a termination condition for our search cycle
Next, when searching at the same depth each time, we need to know how many nodes there are at that depth each time we search.So at the beginning we take a variable to get the queue length, which is the number of nodes in that depth
In the search for each node, we first put the result into the user to find, if the node has been searched before, we skip.If it doesn't exist, place the node in the nodes queue as a basis for the next search, and prevent it from being put in the used list by the next search
To sum up the above ideas, the following is true:

int openLock(vector<string>& deadends,string target)
{
        ....
        int steps = 0;
		while (!nodes.empty())
		{
			steps++;//Depth plus 1
			int size = nodes.size();//Get the total number of nodes
			for (int i = 0; i != size; i++)//Traverse all nodes
			{
				now = nodes.front();
				nodes.pop();
				for (int i = 0; i != 4; i++)//Traverse all possible scenarios where no node changes
				{
					if (used.find(Add(now, i)) == used.end())//If the change is not on the list
					{
						if (Add(now, i) == target)//Eureka
							return steps;
						else {
							used.insert(Add(now, i));
							nodes.push(Add(now, i));//Put it in the next search queue if it's not found and put it in the data it's found
						}
					}
					if (used.find(Sub(now, i)) == used.end())
					{
						if (Sub(now, i) == target)
							return steps;
						else {
							used.insert(Sub(now, i));
							nodes.push(Sub(now, i));
						}
					}
				}
			}
		}
		...
}

All of the above combined:

class Solution {
public:
	int openLock(vector<string>& deadends, string target) {
		string now = "0000";
		set<string> used;
		queue<string> nodes;
		for (int i = 0; i != deadends.size(); i++)
			used.insert(deadends[i]);
		if (used.find("0000") != used.end() || used.find(target) != used.end())
			return -1;
		nodes.push(now);
		used.insert(now);
		int steps = 0;
		while (!nodes.empty())
		{
			steps++;
			int size = nodes.size();
			for (int i = 0; i != size; i++)
			{
				now = nodes.front();
				nodes.pop();
				for (int i = 0; i != 4; i++)
				{
					if (used.find(Add(now, i)) == used.end())
					{
						if (Add(now, i) == target)
							return steps;
						else {
							used.insert(Add(now, i));
							nodes.push(Add(now, i));
						}
					}
					if (used.find(Sub(now, i)) == used.end())
					{
						if (Sub(now, i) == target)
							return steps;
						else {
							used.insert(Sub(now, i));
							nodes.push(Sub(now, i));
						}
					}
				}
			
			}
		}
		return -1;
	}
private:
	inline string Add(string num,int i)
	{
		num[i] = (num[i] - 47) % 10 + 48;
		return num;
	}
	inline string Sub(string num,int i)
	{
		num[i] = (num[i] - 39) % 10 + 48;
		return num;
	}
};

Put it in the main function to test

int main()
{
	Solution solu;
	while (true)
	{
		int size;
	    string target;
		cin >> size >> target;
		vector<string> dead(size);
		for (int i = 0; i != size; i++)
		{
			cin >> dead[i];
		}
		cout << solu.openLock(dead, target);
	}
}

Looks like it's okay?