Why do I need large plus or minus classes?

For computers, the basic data type is generally up to 64-bit data representation range, this range is limited, can not represent all the data infinitely, then is there a way to represent all the large numbers, and complete the addition, subtraction, multiplication and division?

The answer is yes, because the data consists of one digit, so we can simulate most of them simply by using each digit in the array to represent one digit.

So do we need to use large-number simulation when explaining? For contestants, there are many topics that are actually high-precision large-number simulation types. For ordinary programmers, large-number simulation is just the best strategy to do some logical operation and guarantee that it will not overflow, so don't you wonder how to implement a large-number simulation class?

Now start by encapsulating a simple add and subtract class to understand how such a large number simulation works👀

Large Addition and Subtraction Classes for Detailed Implementation

1. Overview of flowcharts

• As a whole, the figure is divided into five parts:

1. Static member functions: public interfaces belonging to classes (core)
2. Constructor and destructor: Construct and destruct objects
3. Member data: data used for operations and data representing objects
4. Operator overloading: for custom operations (core)
5. Internal member function: the public interface that belongs to the object

Detailed explanation of member data and constructors

1. Member data

    bool f;			//Marker for negative numbers
    char *nums;		//Store large, unsigned bits
    int length;		//nums data length
    int capacity;	//Available capacity of nums

1. Construction and Destruction

//Default constructor
BigInteger() : length(0), capacity(1), f(false) { 
        nums = new char[capacity];
    }
//Constructor for converting normal strings
BigInteger(const char *n) : length(strlen(n)), f(false) { 
        int start = 0;
        if (n[0] == '-') {
            f = true;
            start++;
        }
        while (start<length&&n[start] == '0')start++;
        capacity = length * 10;
        nums = new char[capacity];
        std::copy(n + start, n + length, nums);
        length = length - start;
}
//copy constructor
BigInteger(BigInteger &a) {  
        capacity = a.capacity;
        length = a.length;
        f = a.f;
        nums = new char[capacity];
        std::copy(a.nums, a.nums + length, nums);
}
//Move Constructor: An equal sign is called here, which determines which equal sign to use depending on the type of a
BigInteger(BigInteger &&a) :length(0){
        *this = a;
}
//Destructor
~BigInteger() { 
        delete[] nums;
}

3. Detailed explanation of static member functions and operator overloads (algorithm core)

static Swap()

//swap calling std to exchange basic data
static void Swap(BigInteger &a, BigInteger &b) {
        std::swap(a.length, b.length);
        std::swap(a.capacity, b.capacity);
        std::swap(a.f, b.f);
        std::swap(a.nums, b.nums);
}

static compare()

//Compare nums size regardless of symbol: indicates whether a is larger than b
static bool compare(const BigInteger &a,const BigInteger &b) { //Compare pure nums size (no symbols)
        int n1 = a.length;
        int n2 = b.length;
        if (n1 != n2)return n1 > n2; //Returns which is the largest of a and b, and true is the largest of a bits
        int i = 0;
        while (i < n1 && a.nums[i] == b.nums[i])i++; //Compare two values if a b is the same length
        if (i == n1)
            return false;
        return a.nums[i] > b.nums[i];
}

static isEqual()

//Indicates whether a and b are equal
bool isEqual(BigInteger &a, BigInteger &b) {
        if (a.f != b.f || (a.length != b.length))return false;
        int i = 0;
        while (i < a.length && a.nums[i] == b.nums[i])i++;
        return i == a.length && a.f == b.f;
}

(*Core algorithm) static add()

Regardless of the addition of symbols, symbols are controlled by overloaded addition operators.

static BigInteger add(BigInteger &a, BigInteger &b) { //Addition without regard to symbols
    a.reverse();//End alignment
    b.reverse();
    BigInteger t;
    int up = 0;
    int len = a.length > b.length ? a.length : b.length;
    for (int i = 0; i < len; i++) {
        int ta = i < a.length ? a[i] - '0' : 0;
        int tb = i < b.length ? b[i] - '0' : 0;
        int base = ta + tb + up;
        t.push_back(base % 10 + '0');
        up = base / 10;
    }
    if (up)
        t.push_back(up + '0');
    t.reverse();//Return to original position
    a.reverse();
    b.reverse();
    return t;
}

(*Core algorithm) static minus()

Ignoring the subtraction of the symbol, the default nums size of a (regardless of the symbol) is larger than b.

static BigInteger minus(BigInteger &a, BigInteger &b) {
    a.reverse();
    b.reverse();
    BigInteger t;
    int len = a.length > b.length ? a.length : b.length;
    for (int i = 0; i < len; i++) {
        int ta = i < a.length ? a[i] - '0' : 0;
        int tb = i < b.length ? b[i] - '0' : 0;
        int base = ta - tb;
        if (base < 0) {
            base += 10;
            a[i + 1]--;
        }
        t.push_back(base + '0');
    }
    t.reverse();
    a.reverse();
    b.reverse();
    return t;
}

char &operator[]

char &operator[](int i) {
        return nums[i];
}

BigInteger &operator=

Two versions were used - right and left reference versions

• Right-value references extend lifetime and are exchanged (after all, dead values)

BigInteger &operator=(BigInteger&& a) { //Swap&Copy for Right Value Assignment Overload
    Swap(*this, a);
    return *this;
}

• Left value refers to deep copy

BigInteger &operator=(const BigInteger &a) {//deep copy
        if (length != 0)//If it's not an initialization call=, you must delete the original memory first
            delete[]nums;
        capacity = a.capacity;
        length = a.length;
        f = a.f;
        nums = new char[capacity];
        std::copy(a.nums, a.nums + length, nums);
        return *this;
}

bool operator<

Overrides the less than sign, which allows you to sort directly using stl.

Note: Be sure to write as a member function of the const version, otherwise the STL library cannot be called, because all comparisons in the STL library are based on const objects.

bool operator<(const BigInteger &a) const {
        if (f && !a.f) { //One is negative, the other is smaller
            return true;
        } else if (!f && a.f)
            return false;
        if (f) { //Negative for both, true for larger values on the left
            return compare(*this, a);
        }//Both are positive, the smaller values are true on the left
        return compare(a, *this);
}

(*Core algorithm) BigInteger operator+

Unsigned additions and subtractions are accomplished using static member functions, and then various symbol situations are judged here, and different additions are processed according to different symbol situations.

• Note that before calling minus, you need to compare two numbers of nums who is larger and put the larger on the first parameter!

BigInteger operator+(BigInteger &a) {
        BigInteger res;
        bool flag;
        if (a.f && f) { //In the case of negative numbers, add them directly and change the symbol
            res = add(*this, a);
            flag = true;
        } else if (a.f && !f) {//Left plus right minus
            if (compare(a, *this)) { //See if nums corresponding to negative numbers are larger than positive numbers
                flag = true;
                res = minus(a, *this);
            } else {
                flag = false;
                res = minus(*this, a);
            }
        } else if (!a.f && f) {
            if (compare(*this, a)) { //Same as previous
                flag = true;
                res = minus(*this, a);
            } else {
                flag = false;
                res = minus(a, *this);
            }
        } else { //Simultaneously positive numbers are the simplest addition
            flag = false;
            res = add(*this, a);
        }
        res.f = flag;
        return res;
}

(*Core algorithm) BigInteger operator-

It's also a categorical discussion, calling the minus and add functions according to different types.

• Unlike positive numbers, symbols are treated differently. If they are both negative numbers, they need to be judged to be equal, preventing the two numbers from being equal, subtracted from zero, and processed to -0.

BigInteger operator-(BigInteger &a) {
        BigInteger res;
        bool flag;
        if (a.f && f) { //In the same negative case--left-right== (no sign) right - (no sign) left
            if (compare(a, *this)) {
                flag = false;
                res = minus(a, *this);
            } else {
                if (isEqual(*this, a))
                    flag = false;
                else flag = true;
                res = minus(*this, a);
            }
        } else if (a.f && !f) { //Positive left, negative right--Left-Right==Left+Right
            flag = false;
            res = add(a, *this);
        } else if (!a.f && f) { //Positive on the right and negative on the left--Left-Right==Negative addition on both sides
            flag = true;
            res = add(a, *this);
        } else { //Simultaneously positive--Left-Right==Left-Right (category discussion positive and negative)
            if (compare(a, *this)) { //Right > Left, negative sign
                res = minus(a, *this);
                flag = true;
            } else { //Right < Left, Positive Symbol
                res = minus(*this, a);
                flag = false;
            }
        }
        res.f = flag;
        return res;
}

4. Detailed explanation of other internal member functions

1. Outgoing get interface

  int getCap() {
        return capacity;
    }

    int getLength() {
        return length;
    }

    bool isNegative() {
        return f;
    }

    bool isEmpty() {
        return length == 0;
    }

1. push_back and reverse functions necessary for assignment

    void push_back(char x) {
        if (length >= capacity) {//Expansion operation
            capacity *= 2;
            char *t = nums;
            nums = new char[capacity];
            std::copy(t, t + length, nums);
            delete[]t;
        }
        nums[length++] = x;
    }

    void reverse() {//Reverse operation
        int l = 0, r = length - 1;
        while (l < r) {
            std::swap(nums[l], nums[r]);
            l++;
            r--;
        }
    }

1. Important read() input interface and print() output test interface

    void print() {
        if (f)
            printf("-");
        nums[length] = '\0';
        int i = 0;
        while (nums[i] == '0')i++;
        printf("%s", nums + i);
    }

    void read() {//Assigning data to objects using getchar()
        char c = getchar();
        if (c == '-') {
            f = true;
            c = getchar();
        }
        while (c == '0') c = getchar();//Consume Lead 0
        while (c != '\n') {
            push_back(c);//Constantly calling push_back
            c = getchar();
        }
    }

Organize Code

.h declaration file

If a class is defined at the same time as it is declared, the internal member functions are inlined by default, so we usually inline short code, and the following implementations follow this rule.

//
// Created by Alone on 2021/10/7.
//

#ifndef MY_TINY_STL_BIGINTEGER_H
#define MY_TINY_STL_BIGINTEGER_H

#include <algorithm>
#include <iostream>
#include <cstring>

class BigInteger {
    bool f;
    char *nums;
    int length;
    int capacity;
public:
    //Constructor
    BigInteger() : length(0), capacity(1), f(false) { //Default constructor
        nums = new char[capacity];
    }

    BigInteger(const char *n);

    BigInteger(const BigInteger &a);

    BigInteger(BigInteger &&a);

    ~BigInteger() { //Destructor
        delete[] nums;
    }

public:
    //Static function
    static void Swap(BigInteger &a, BigInteger &b);

    static bool compare(const BigInteger &a, const BigInteger &b);

    bool isEqual(BigInteger &a, BigInteger &b);

    static BigInteger add(BigInteger &a, BigInteger &b);

    static BigInteger minus(BigInteger &a, BigInteger &b);

public:
    //Operator overloading
    char &operator[](int i) {
        return nums[i];
    }

    BigInteger &operator=(BigInteger &&a) { //Swap&Copy for Right Value Assignment Overload
        Swap(*this, a);
        return *this;
    }

    BigInteger &operator=(const BigInteger &a);

    bool operator<(const BigInteger &a) const;

    BigInteger operator+(BigInteger &a);

    BigInteger operator-(BigInteger &a);

public:
    //Basic member functions of objects
    int getCap() {
        return capacity;
    }

    int getLength() {
        return length;
    }

    bool isNegative() {
        return f;
    }

    bool isEmpty() {
        return length == 0;
    }

    void reverse();

    void push_back(char x);

    void print();

    void read();
};


#endif //MY_TINY_STL_BIGINTEGER_H

.cpp definition and Implementation

//
// Created by Alone on 2021/10/7.
//

#include "BigInteger.h"

//@Constructor Implementation
BigInteger::BigInteger(const char *n) : length(strlen(n)), f(false) { //Constructor for Initial Value
    int start = 0;
    if (n[0] == '-') {
        f = true;
        start++;
    }
    while (start < length && n[start] == '0')start++;
    capacity = length * 10;
    nums = new char[capacity];
    std::copy(n + start, n + length, nums);
    length = length - start;
}

BigInteger::BigInteger(const BigInteger &a) {  //copy constructor
    capacity = a.capacity;
    length = a.length;
    f = a.f;
    nums = new char[capacity];
    std::copy(a.nums, a.nums + length, nums);
}

BigInteger::BigInteger(BigInteger &&a) : length(0) { //move constructor
    *this = a;
}

//@Static function implementation
void BigInteger::Swap(BigInteger &a, BigInteger &b) {
    std::swap(a.length, b.length);
    std::swap(a.capacity, b.capacity);
    std::swap(a.f, b.f);
    std::swap(a.nums, b.nums);
}

bool BigInteger::compare(const BigInteger &a, const BigInteger &b) {
    int n1 = a.length;
    int n2 = b.length;
    if (n1 != n2)return n1 > n2; //Returns which is the largest of a and b, and true is the largest of a bits
    int i = 0;
    while (i < n1 && a.nums[i] == b.nums[i])i++; //Compare two values if a b is the same length
    if (i == n1)
        return false;
    return a.nums[i] > b.nums[i];
}

bool BigInteger::isEqual(BigInteger &a, BigInteger &b) {
    if (a.f != b.f || (a.length != b.length))return false;
    int i = 0;
    while (i < a.length && a.nums[i] == b.nums[i])i++;
    return i == a.length && a.f == b.f;
}

BigInteger BigInteger::add(BigInteger &a, BigInteger &b) {
    a.reverse();//End alignment
    b.reverse();
    BigInteger t;
    int up = 0;
    int len = a.length > b.length ? a.length : b.length;
    for (int i = 0; i < len; i++) {
        int ta = i < a.length ? a[i] - '0' : 0;
        int tb = i < b.length ? b[i] - '0' : 0;
        int base = ta + tb + up;
        t.push_back(base % 10 + '0');
        up = base / 10;
    }
    if (up)
        t.push_back(up + '0');
    t.reverse();//Return to original position
    a.reverse();
    b.reverse();
    return t;
}

BigInteger BigInteger::minus(BigInteger &a, BigInteger &b) {
    a.reverse();
    b.reverse();
    BigInteger t;
    int len = a.length > b.length ? a.length : b.length;
    for (int i = 0; i < len; i++) {
        int ta = i < a.length ? a[i] - '0' : 0;
        int tb = i < b.length ? b[i] - '0' : 0;
        int base = ta - tb;
        if (base < 0) {
            base += 10;
            a[i + 1]--;
        }
        t.push_back(base + '0');
    }
    t.reverse();
    a.reverse();
    b.reverse();
    return t;
}


//@Operator overload implementation
BigInteger &BigInteger::operator=(const BigInteger &a) {
    if (length != 0)//If it's not an initialization call=, you must delete the original memory first
        delete[]nums;
    capacity = a.capacity;
    length = a.length;
    f = a.f;
    nums = new char[capacity];
    std::copy(a.nums, a.nums + length, nums);
    return *this;
}

BigInteger BigInteger::operator+(BigInteger &a) {
    BigInteger res;
    bool flag;
    if (a.f && f) { //In the case of negative numbers, add them directly and change the symbol
        res = add(*this, a);
        flag = true;
    } else if (a.f && !f) {//Left plus right minus
        if (compare(a, *this)) { //See if nums corresponding to negative numbers are larger than positive numbers
            flag = true;
            res = minus(a, *this);
        } else {
            flag = false;
            res = minus(*this, a);
        }
    } else if (!a.f && f) {
        if (compare(*this, a)) { //Same as previous
            flag = true;
            res = minus(*this, a);
        } else {
            flag = false;
            res = minus(a, *this);
        }
    } else { //Simultaneously positive numbers are the simplest addition
        flag = false;
        res = add(*this, a);
    }
    res.f = flag;
    return res;
}

BigInteger BigInteger::operator-(BigInteger &a) {
    BigInteger res;
    bool flag;
    if (a.f && f) { //In the same negative case--left-right== (no sign) right - (no sign) left
        if (compare(a, *this)) {
            flag = false;
            res = minus(a, *this);
        } else {
            if (isEqual(*this, a))
                flag = false;
            else flag = true;
            res = minus(*this, a);
        }
    } else if (a.f && !f) { //Positive left, negative right--Left-Right==Left+Right
        flag = false;
        res = add(a, *this);
    } else if (!a.f && f) { //Positive on the right and negative on the left--Left-Right==Negative addition on both sides
        flag = true;
        res = add(a, *this);
    } else { //Simultaneously positive--Left-Right==Left-Right (category discussion positive and negative)
        if (compare(a, *this)) { //Right > Left, negative sign
            res = minus(a, *this);
            flag = true;
        } else { //Right < Left, Positive Symbol
            res = minus(*this, a);
            flag = false;
        }
    }
    res.f = flag;
    return res;
}

bool BigInteger::operator<(const BigInteger &a) const {
    if (f && !a.f) { //One is negative, the other is smaller
        return true;
    } else if (!f && a.f)
        return false;
    if (f) { //Negative for both, true for larger values on the left
        return compare(*this, a);
    }//Both are positive, the smaller values are true on the left
    return compare(a, *this);
}


//@Basic member function
void BigInteger::reverse() {
    int l = 0, r = length - 1;
    while (l < r) {
        std::swap(nums[l], nums[r]);
        l++;
        r--;
    }
}

void BigInteger::push_back(char x) {
    if (length >= capacity) {
        capacity *= 2;
        char *t = nums;
        nums = new char[capacity];
        std::copy(t, t + length, nums);
        delete[]t;
    }
    nums[length++] = x;
}

void BigInteger::print() {
    if (f)
        printf("-");
    nums[length] = '\0';
    int i = 0;
    while (nums[i] == '0')i++;
    printf("%s", nums + i);
}

void BigInteger::read() {
    char c = getchar();
    if (c == '-') {
        f = true;
        c = getchar();
    }
    while (c == '0') c = getchar();//Consume Lead 0
    while (c != '\n') {
        push_back(c);//Constantly calling push_back
        c = getchar();
    }
}

functional testing

1. Basic Addition and Subtraction Testing

Running test code:

Print Output

python output

• summary

As with python output, it passes the test, but it is not very persuasive because there are too few test data, and there are later problem solving tests.

2. Store Personal Input Data + Sort Test

Test code (10 data entered for easy testing):

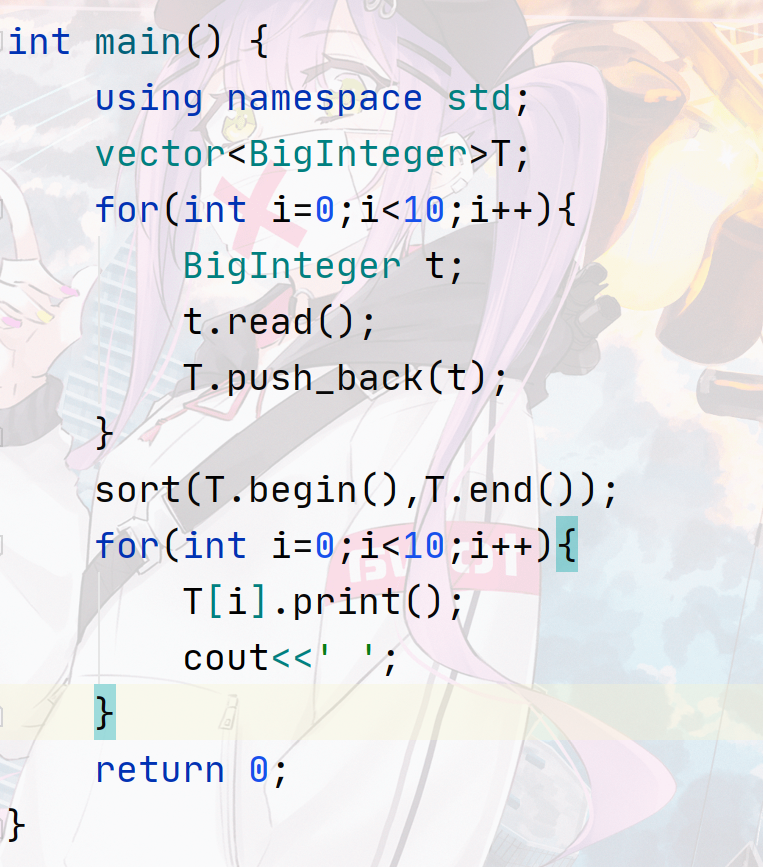
Sort output:

3. Problem-solving test

The PAT Class A just recently brushed involves adding or subtracting hhh for large numbers!
Title Description

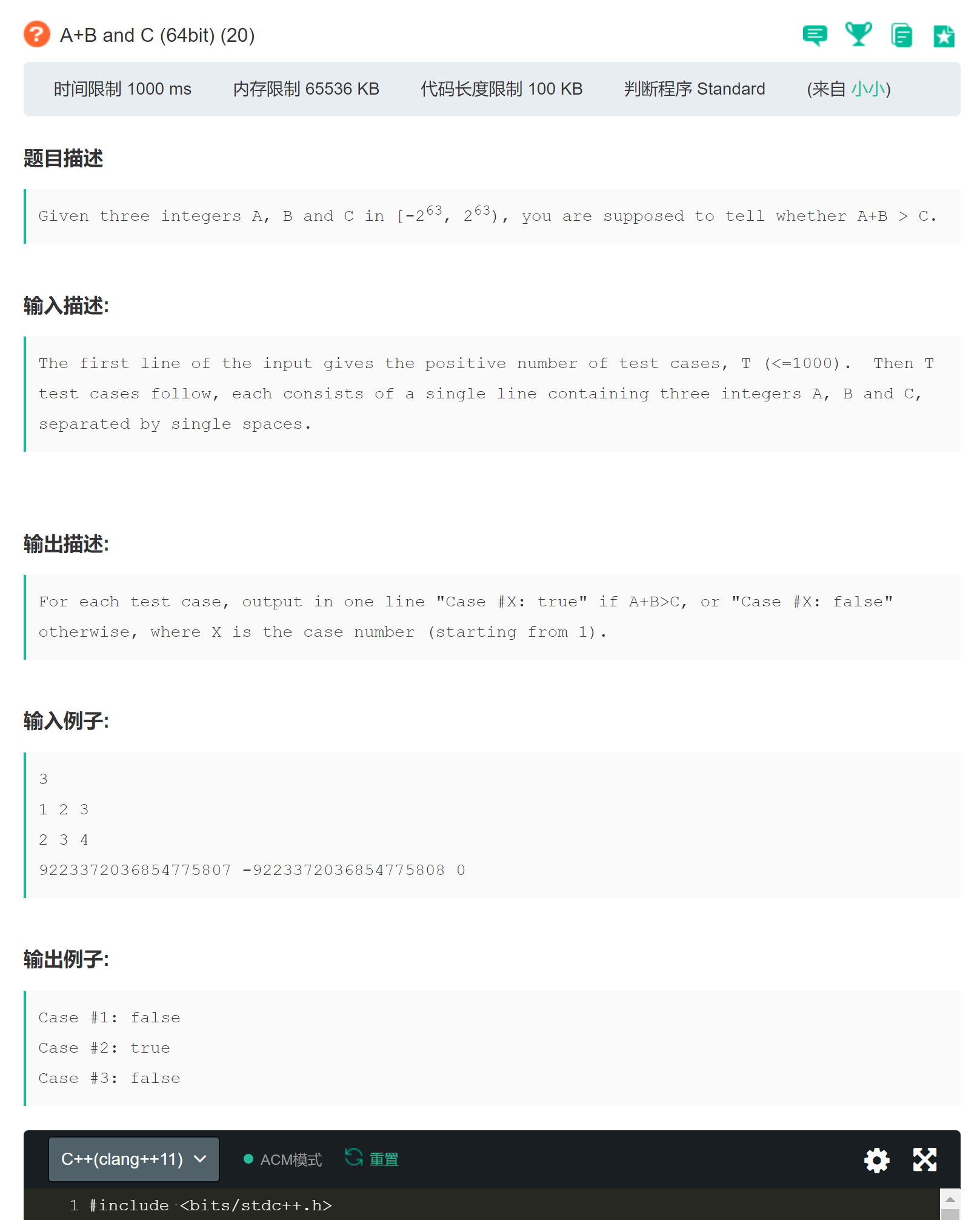
OJ Platform

Problem solving code

#include "bits/stdc++.h"

class BigInteger {
    bool f;
    char *nums;
    int length;
    int capacity;
public://Constructor
    BigInteger() : length(0), capacity(1), f(false) { //Default constructor
        nums = new char[capacity];
    }

    BigInteger(const char *n) : length(strlen(n)), f(false) { //Constructor for Initial Value
        int start = 0;
        if (n[0] == '-') {
            f = true;
            start++;
        }
        while (start < length && n[start] == '0')start++;
        capacity = length * 10;
        nums = new char[capacity];
        std::copy(n + start, n + length, nums);
        length = length - start;
    }

    BigInteger(const BigInteger &a) {  //copy constructor
        capacity = a.capacity;
        length = a.length;
        f = a.f;
        nums = new char[capacity];
        std::copy(a.nums, a.nums + length, nums);
    }

    BigInteger(BigInteger &&a) : length(0) { //move constructor
        *this = a;
    }

    ~BigInteger() { //Destructor
        delete[] nums;
    }

public://Static member function
    static void Swap(BigInteger &a, BigInteger &b) {
        std::swap(a.length, b.length);
        std::swap(a.capacity, b.capacity);
        std::swap(a.f, b.f);
        std::swap(a.nums, b.nums);
    }

    static bool compare(const BigInteger &a, const BigInteger &b) { //Compare pure nums size (no symbols)
        int n1 = a.length;
        int n2 = b.length;
        if (n1 != n2)return n1 > n2; //Returns which is the largest of a and b, and true is the largest of a bits
        int i = 0;
        while (i < n1 && a.nums[i] == b.nums[i])i++; //Compare two values if a b is the same length
        if (i == n1)
            return false;
        return a.nums[i] > b.nums[i];
    }

    bool isEqual(BigInteger &a, BigInteger &b) {
        if (a.f != b.f || (a.length != b.length))return false;
        int i = 0;
        while (i < a.length && a.nums[i] == b.nums[i])i++;
        return i == a.length && a.f == b.f;
    }

    static BigInteger add(BigInteger &a, BigInteger &b) { //Addition without regard to symbols
        a.reverse();//End alignment
        b.reverse();
        BigInteger t;
        int up = 0;
        int len = a.length > b.length ? a.length : b.length;
        for (int i = 0; i < len; i++) {
            int ta = i < a.length ? a[i] - '0' : 0;
            int tb = i < b.length ? b[i] - '0' : 0;
            int base = ta + tb + up;
            t.push_back(base % 10 + '0');
            up = base / 10;
        }
        if (up)
            t.push_back(up + '0');
        t.reverse();//Return to original position
        a.reverse();
        b.reverse();
        return t;
    }

    static BigInteger minus(BigInteger &a, BigInteger &b) { //Ignoring the subtraction of the symbol, the default is that the length or size of a is larger than b (so don't call it indiscriminately outside)
        a.reverse();
        b.reverse();
        BigInteger t;
        int len = a.length > b.length ? a.length : b.length;
        for (int i = 0; i < len; i++) {
            int ta = i < a.length ? a[i] - '0' : 0;
            int tb = i < b.length ? b[i] - '0' : 0;
            int base = ta - tb;
            if (base < 0) {
                base += 10;
                a[i + 1]--;
            }
            t.push_back(base + '0');
        }
        t.reverse();
        a.reverse();
        b.reverse();
        return t;
    }

public://Member functions and overloaded operators
    char &operator[](int i) {
        return nums[i];
    }

    BigInteger &operator=(BigInteger &&a) { //Swap&Copy for Right Value Assignment Overload
        Swap(*this, a);
        return *this;
    }

    BigInteger &operator=(const BigInteger &a) {//deep copy
        if (length != 0)//If it's not an initialization call=, you must delete the original memory first
            delete[]nums;
        capacity = a.capacity;
        length = a.length;
        f = a.f;
        nums = new char[capacity];
        std::copy(a.nums, a.nums + length, nums);
        return *this;
    }

    int getCap() {
        return capacity;
    }

        int getLength() {
            return length;
        }

    bool isNegative() {
        return f;
    }

    bool isEmpty() {
        return length == 0;
    }

    void reverse() {
        int l = 0, r = length - 1;
        while (l < r) {
            std::swap(nums[l], nums[r]);
            l++;
            r--;
        }
    }

    void push_back(char x) {
        if (length >= capacity) {
            capacity *= 2;
            char *t = nums;
            nums = new char[capacity];
            std::copy(t, t + length, nums);
            delete[]t;
        }
        nums[length++] = x;
    }

    bool operator<(const BigInteger &a) const {
        if (f && !a.f) { //One is negative, the other is smaller
            return true;
        } else if (!f && a.f)
            return false;
        if (f) { //Negative for both, true for larger values on the left
            return compare(*this, a);
        }//Both are positive, the smaller values are true on the left
        return compare(a, *this);
    }

    BigInteger operator+(BigInteger &a) {
        BigInteger res;
        bool flag;
        if (a.f && f) { //In the case of negative numbers, add them directly and change the symbol
            res = add(*this, a);
            flag = true;
        } else if (a.f && !f) {//Left plus right minus
            if (compare(a, *this)) { //See if nums corresponding to negative numbers are larger than positive numbers
                flag = true;
                res = minus(a, *this);
            } else {
                flag = false;
                res = minus(*this, a);
            }
        } else if (!a.f && f) {
            if (compare(*this, a)) { //Same as previous
                flag = true;
                res = minus(*this, a);
            } else {
                flag = false;
                res = minus(a, *this);
            }
        } else { //Simultaneously positive numbers are the simplest addition
            flag = false;
            res = add(*this, a);
        }
        res.f = flag;
        return res;
    }

    BigInteger operator-(BigInteger &a) {
        BigInteger res;
        bool flag;
        if (a.f && f) { //In the same negative case--left-right== (no sign) right - (no sign) left
            if (compare(a, *this)) {
                flag = false;
                res = minus(a, *this);
            } else {
                if (isEqual(*this, a))
                    flag = false;
                else flag = true;
                res = minus(*this, a);
            }
        } else if (a.f && !f) { //Positive left, negative right--Left-Right==Left+Right
            flag = false;
            res = add(a, *this);
        } else if (!a.f && f) { //Positive on the right and negative on the left--Left-Right==Negative addition on both sides
            flag = true;
            res = add(a, *this);
        } else { //Simultaneously positive--Left-Right==Left-Right (category discussion positive and negative)
            if (compare(a, *this)) { //Right > Left, negative sign
                res = minus(a, *this);
                flag = true;
            } else { //Right < Left, Positive Symbol
                res = minus(*this, a);
                flag = false;
            }
        }
        res.f = flag;
        return res;
    }

    void print() {
        if (f)
            printf("-");
        nums[length] = '\0';
        int i = 0;
        while (nums[i] == '0')i++;
        printf("%s", nums + i);
    }

    void read() {//Assigning data to objects using getchar()
        char c = getchar();
        if (c == '-') {
            f = true;
            c = getchar();
        }
        while (c=='\n'||c == '0'||c == ' ') c = getchar();//Consume leading 0 and spaces
        while (c != '\n'&&c != ' '&& c != '\t') {
            push_back(c);//Constantly calling push_back
            c = getchar();
        }
    }
};

int main() {
    using namespace std;
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        char a[100], b[100], c[100];
        printf("Case #%d: ", i);
        cin >> a >> b >> c;
        BigInteger a1(a), b2(b), c2(c);
        BigInteger t = c2 - b2;
        if (t < a1)
            cout << "true\n";
        else cout << "false\n";
    }
    return 0;
}

Correct output

summary

Many people may think that doing a project must be that tall, or that kind of snake-eating or Minesweeper game. In fact, as long as you are interested, anything can become your practice project, and the benefits may be greater than you go with the wind to make a few small games.

The main benefit of this project is that I have a better understanding of C++ syntax, a clearer understanding of mobile constructors, copy constructors, assignment overloads, and the most important one is to strengthen the design thinking of a class.

Writing more implementations of classes is not only conducive to the understanding of algorithms and language grammar, but also to the design ideas of each function. As programmers, what we need most is such logical thinking. From the beginning of receiving demand, we should be able to quickly Abstract various implementations, and then continue to optimize them to get our own code!