Basic problems related to binary tree

1. To realize the traversal of binary tree in the order of first, middle and last, including recursive and non recursive ways
2. Find the successor node of a node in a binary tree
3. Serialization and deserialization of binary tree
4. Binary tree serialization by layer
5. Is a binary tree a balanced binary tree?
6. Is a tree a search binary tree? Is a tree a complete binary tree?
7. Given a complete binary tree, how many nodes is it?
   (Section 5 of Zuoshen algorithm primary class)

1. Implement the traversal of binary tree in the order of first, middle and last, including recursive and non recursive ways

1) Recursive way to achieve first order, middle order, and then order traversal
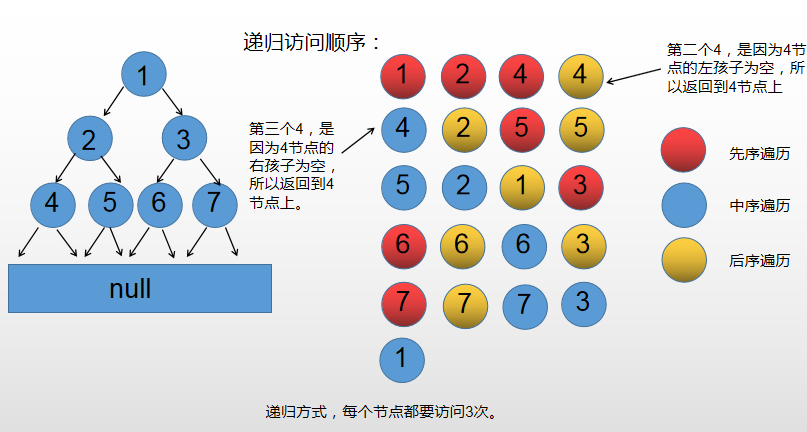
Different printing time and different order traversal

• Preorder traversal: print the first visited node
• Middle order traversal: print the second visited node
• Post order traversal: print nodes visited for the third time

Code:

public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static void preOrderRecur(Node head) {//Preorder traversal
		if (head == null) {
			return;
		}
		System.out.print(head.value + " ");
		preOrderRecur(head.left);
		preOrderRecur(head.right);
	}

	public static void inOrderRecur(Node head) {//Sequential traversal
		if (head == null) {
			return;
		}
		inOrderRecur(head.left);
		System.out.print(head.value + " ");
		inOrderRecur(head.right);
	}

	public static void posOrderRecur(Node head) {//Post order traversal
		if (head == null) {
			return;
		}
		posOrderRecur(head.left);
		posOrderRecur(head.right);
		System.out.print(head.value + " ");
	}

2) Non recursive mode (stack):
Sequence traversal: stack pressing

• Press the right child first and then the left child

public static void preOrderUnRecur(Node head) {
		System.out.print("pre-order: ");
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			stack.add(head);
			while (!stack.isEmpty()) {
				head = stack.pop();
				System.out.print(head.value + " ");
				if (head.right != null) {//Right first
					stack.push(head.right);
				}
				if (head.left != null) {//
					stack.push(head.left);
				}
			}
		}
		System.out.println();
	}

Middle order traversal:
Explanation 1:

• If the current node is empty, take a print from the stack, and the current node is to the right
• If the current node is not empty, the current node is pushed into the stack, and the current node is to the left
  Explanation two:
• If there are left children, press all the left children into the stack at one time, and then pop them up one by one
• If there are left children in the right child tree of the pop-up node, all the left children in the right child tree will be pushed into the stack again.
• Repeat until there are no elements in the stack

public static void inOrderUnRecur(Node head) {//Non recursive way: middle order traversal
		System.out.print("in-order: ");
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			while (!stack.isEmpty() || head != null) {
				if (head != null) {
					stack.push(head);
					head = head.left;
				} else {
					head = stack.pop();
					System.out.print(head.value + " ");
					head = head.right;
				}
			}
		}
		System.out.println();
	}

Backward traversal (left then right, middle):

• Using two stacks, we can use one stack to achieve first order traversal, first print the middle node, then print the left subtree, and finally print the right subtree (when the code is implemented by stack, first press the right, then press the left);
• Then we can use a stack to print the middle node first, then the right subtree, and finally the left subtree. (when using stack, press left first, then right)
• Then when printing the intermediate node, first press it into another stack, and then print it after traversing.
• The sequence is to traverse the left subtree first, then the right subtree, and finally print.

Code:

public static void posOrderUnRecur1(Node head) {
		System.out.print("pos-order: ");
		if (head != null) {
			Stack<Node> s1 = new Stack<Node>();
			Stack<Node> s2 = new Stack<Node>();
			s1.push(head);
			while (!s1.isEmpty()) {
				head = s1.pop();
				s2.push(head);//Press into the stack and wait for the traversal to finish before printing
				if (head.left != null) {//The first step of stack implementation is right first and then left, so here we need to reverse, left first and then right
					s1.push(head.left);//Press left first
				}
				if (head.right != null) {
					s1.push(head.right);//Repressing right
				}
			}
			while (!s2.isEmpty()) {//Auxiliary stack, print after all nodes are traversed
				System.out.print(s2.pop().value + " ");
			}
		}
		System.out.println();
	}

Use a stack to implement non recursive post order traversal (not required):

public static void posOrderUnRecur2(Node h) {
		System.out.print("pos-order: ");
		if (h != null) {
			Stack<Node> stack = new Stack<Node>();
			stack.push(h);
			Node c = null;
			while (!stack.isEmpty()) {
				c = stack.peek();
				if (c.left != null && h != c.left && h != c.right) {
					stack.push(c.left);
				} else if (c.right != null && h != c.right) {
					stack.push(c.right);
				} else {
					System.out.print(stack.pop().value + " ");
					h = c;
				}
			}
		}
		System.out.println();
	}

2. How to print a binary tree intuitively (not required)

Restore the whole tree in first order and middle order (inconvenient)
For example: restore the binary tree with 1,1,1,1 in the first and middle order (two situations will occur, so it is inconvenient)
resolvent:
Rotate 90 ° anticlockwise

public class Code_02_PrintBinaryTree {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static void printTree(Node head) {
		System.out.println("Binary Tree:");
		printInOrder(head, 0, "H", 17);
		System.out.println();
	}

	public static void printInOrder(Node head, int height, String to, int len) {
		if (head == null) {
			return;
		}
		printInOrder(head.right, height + 1, "v", len);
		String val = to + head.value + to;
		int lenM = val.length();
		int lenL = (len - lenM) / 2;
		int lenR = len - lenM - lenL;
		val = getSpace(lenL) + val + getSpace(lenR);
		System.out.println(getSpace(height * len) + val);
		printInOrder(head.left, height + 1, "^", len);
	}

	public static String getSpace(int num) {
		String space = " ";
		StringBuffer buf = new StringBuffer("");
		for (int i = 0; i < num; i++) {
			buf.append(space);
		}
		return buf.toString();
	}

	public static void main(String[] args) {
		Node head = new Node(1);
		head.left = new Node(-222222222);
		head.right = new Node(3);
		head.left.left = new Node(Integer.MIN_VALUE);
		head.right.left = new Node(55555555);
		head.right.right = new Node(66);
		head.left.left.right = new Node(777);
		printTree(head);

		head = new Node(1);
		head.left = new Node(2);
		head.right = new Node(3);
		head.left.left = new Node(4);
		head.right.left = new Node(5);
		head.right.right = new Node(6);
		head.left.left.right = new Node(7);
		printTree(head);

		head = new Node(1);
		head.left = new Node(1);
		head.right = new Node(1);
		head.left.left = new Node(1);
		head.right.left = new Node(1);
		head.right.right = new Node(1);
		head.left.left.right = new Node(1);
		printTree(head);

	}

}

3. Find the successor node of a node in the binary tree

[Topic] now there is a new node type of binary tree as follows:
public class Node { public int value; public Node left; public Node right; public Node parent; public Node(int data) { this.value = data; } }

This structure has one more parent pointer to the parent node than the normal binary tree node structure. Suppose there is a binary tree composed of nodes of node type. The parent pointer of each node in the tree points to its own parent node correctly, and the parent of the header node points to null. Only for a node node in a binary tree, please implement the function of returning the node's successor node. In the middle order traversal sequence of binary tree, the next node of node is called the successor node of node.

Successor node: the next node in the sequence traversed in the middle order.
Precursor node: the previous node of a node in the sequence traversed in the middle order.

1) Method 1 (traverse the whole tree):
Starting from the initial node, output the middle order traversal, generate the sequence, and observe the next node of one node

2) Method 2:

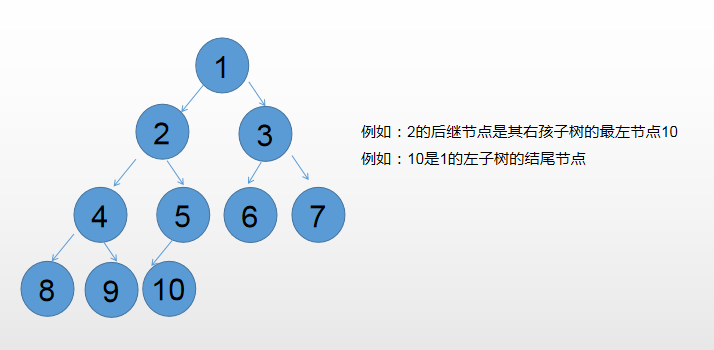
• If a node has a right subtree, its successor node is the leftmost node of its right subtree.
• If the node does not have a right subtree, find which left subtree ends with the node.
  

Code:

public static class Node {
		public int value;
		public Node left;
		public Node right;
		public Node parent;

		public Node(int data) {
			this.value = data;
		}
	}

	public static Node getSuccessorNode(Node node) {
		if (node == null) {
			return node;
		}
		if (node.right != null) {//If there is a right subtree
			return getLeftMost(node.right);
		} else {//There is no right subtree. Find which left subtree ends with this node
			Node parent = node.parent;
			while (parent != null && parent.left != node) {
				node = parent;
				parent = node.parent;
			}
			return parent;
		}
	}

	public static Node getLeftMost(Node node) {//Find the leftmost node of the right subtree
		if (node == null) {
			return node;
		}
		while (node.left != null) {
			node = node.left;
		}
		return node;
	}

4. Introduce the serialization and deserialization of binary tree

1) Sequence traversal serialization and deserialization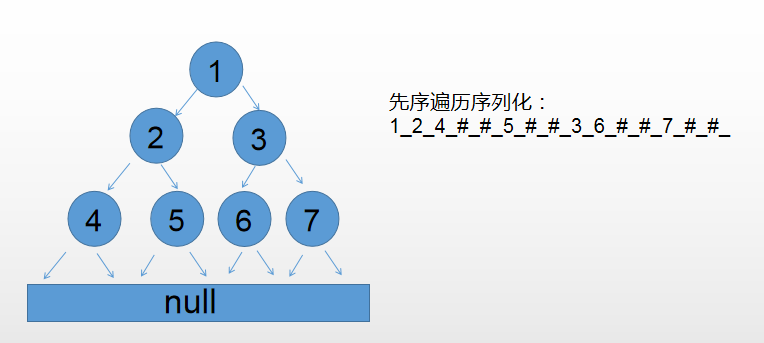

Sequence traversal serialization code:

public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static String serialByPre(Node head) {
		if (head == null) {
			return "#_";
		}
		String res = head.value + "_";
		res += serialByPre(head.left);
		res += serialByPre(head.right);
		return res;
	}

Sequence through deserialization Code:

public static Node reconByPreString(String preStr) {
		String[] values = preStr.split("_");
		Queue<String> queue = new LinkedList<String>();
		for (int i = 0; i != values.length; i++) {
			queue.offer(values[i]);
		}
		return reconPreOrder(queue);
	}

	public static Node reconPreOrder(Queue<String> queue) {
		String value = queue.poll();
		if (value.equals("#")) {
			return null;
		}
		Node head = new Node(Integer.valueOf(value));
		head.left = reconPreOrder(queue);
		head.right = reconPreOrder(queue);
		return head;
	}

2) Serialize, deserialize by layer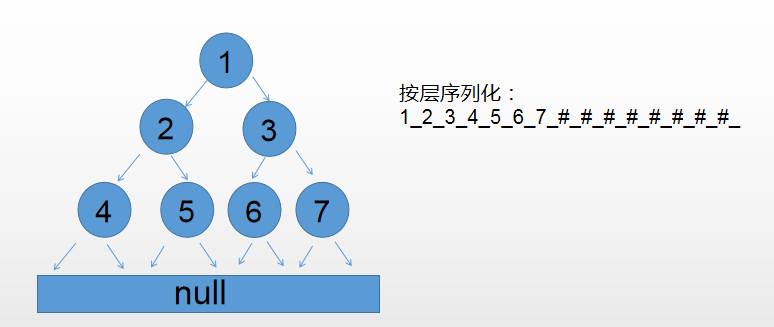

Serialize code by layer:

public static String serialByLevel(Node head) {
		if (head == null) {
			return "#_";
		}
		String res = head.value + "_";
		Queue<Node> queue = new LinkedList<Node>();
		queue.offer(head);
		while (!queue.isEmpty()) {
			head = queue.poll();
			if (head.left != null) {
				res += head.left.value + "_";
				queue.offer(head.left);
			} else {
				res += "#_";
			}
			if (head.right != null) {
				res += head.right.value + "_";
				queue.offer(head.right);
			} else {
				res += "#_";
			}
		}
		return res;
	}

Deserialize code by layer:

public static Node reconByLevelString(String levelStr) {
		String[] values = levelStr.split("_");
		int index = 0;
		Node head = generateNodeByString(values[index++]);
		Queue<Node> queue = new LinkedList<Node>();
		if (head != null) {
			queue.offer(head);
		}
		Node node = null;
		while (!queue.isEmpty()) {
			node = queue.poll();
			node.left = generateNodeByString(values[index++]);
			node.right = generateNodeByString(values[index++]);
			if (node.left != null) {
				queue.offer(node.left);
			}
			if (node.right != null) {
				queue.offer(node.right);
			}
		}
		return head;
	}

	public static Node generateNodeByString(String val) {
		if (val.equals("#")) {
			return null;
		}
		return new Node(Integer.valueOf(val));
	}

5. Judge whether a binary tree is a balanced binary tree

Judging standard of balanced binary tree: the height difference between left and right subtrees of any node is no more than 1

Recursive method code:

public static class ReturnData{
		public boolean isB;
		public int h;
		
		public ReturnData(boolean isB,int h) {
			this.isB=isB;
			this.h=h;
		}
	}
	
	public static boolean isB(Node head) {
		return process(head).isB;
	}
	
	public static ReturnData process(Node head) {
		if(head==null) {
			return new ReturnData(true,0);
		}
		ReturnData leftData = process(head.left);
		if(!leftData.isB) {
			return new ReturnData(false,0);
		}
		ReturnData rightData = process(head.right);
		if(!rightData.isB) {
			return new ReturnData(false,0);
		}
		if(Math.abs(leftData.h-rightData.h)>1) {//Judge whether the height difference between left and right subtrees exceeds 1
			return new ReturnData(false,0);
		}
		return new ReturnData(true,Math.max(leftData.h, rightData.h)+1);//Return to current height
	}

6. Judge whether a tree is a search binary tree and whether a tree is a complete binary tree

1) Search Binary Tree: for any node, the left subtree is smaller than it, and the right subtree is larger than it.
Judge the search criteria of binary tree (no duplicate nodes): whether the sequence of middle order traversal of binary tree is in ascending order

public static boolean inOrderUnRecur(Node head) {//Non recursive way: middle order traversal changes to judge whether it is a search Binary Tree
		System.out.print("in-order: ");
		int pre = Integer.MIN_VALUE;
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			while (!stack.isEmpty() || head != null) {
				if (head != null) {
					stack.push(head);
					head = head.left;
				} else {
					head = stack.pop();
					if(head.value<pre) {
						return false;
					}
					pre = head.value;
					head = head.right;
				}
			}
		}
		return true;
	}

2) Complete binary tree:
Judgment logic: traverse by layer

• If there is a right child without a left child, it is not a complete binary tree;
• If it is not the left and right children's double complete, all nodes encountered later must be leaf nodes, otherwise it is not a complete binary tree.
• If these situations don't occur in one traverse, it is a complete binary tree.

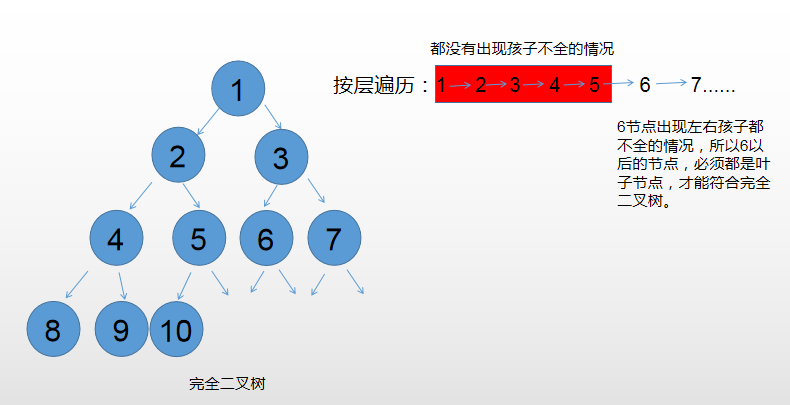
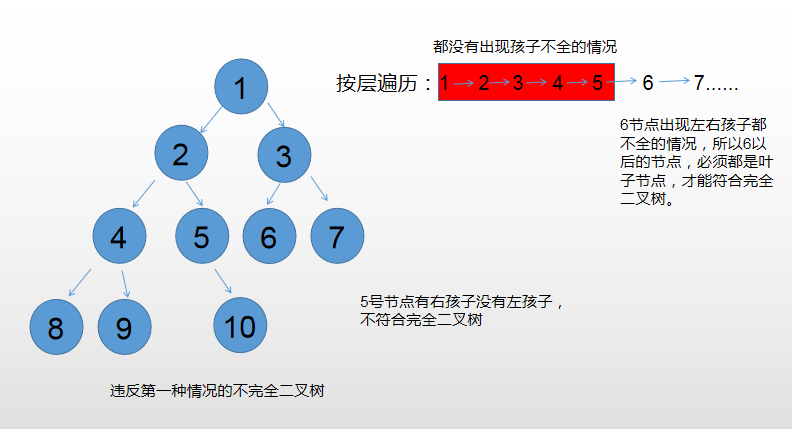
Determine the complete binary tree code:

public static boolean isCBT(Node head) {
		if (head == null) {
			return true;
		}
		Queue<Node> queue = new LinkedList<Node>();//Queue structure
		boolean leaf = false;//Whether to start the leaf stage, i.e. all subsequent nodes must be leaf nodes
		Node l = null;
		Node r = null;
		queue.offer(head);
		while (!queue.isEmpty()) {
			head = queue.poll();
			l = head.left;
			r = head.right;
			if ((leaf && (l != null || r != null)) 
					|| 
					(l == null && r != null)) {//If the left child is empty, the right child is not empty. If the leaf stage is opened, the left and right children cannot have
				return false;
			}
			if (l != null) {//If left is not empty, enter the queue
				queue.offer(l);
			}
			if (r != null) {//If the right is not empty, enter the queue
				queue.offer(r);
			} else {//If left child or right child is empty, open leaf stage
				leaf = true;
			}
		}
		return true;
	}

7. Given a complete binary tree, find the number of nodes

Requirement: time complexity is lower than O(N), N is the number of nodes in this tree
Note: binary tree cannot be traversed, otherwise the time complexity is higher than O(N)

Solve recursively:

• If the height of a full binary tree is h, the number of nodes is 2 H-1.
• Traverse the left boundary of the tree to find the height h1 (the cost is O(logN)).
• Traverse the left boundary of the right subtree, find the height H 2 (the cost becomes O(logN)2), and judge whether it is equal to h 1.
• If H1 and h2 are equal, the left subtree of a full binary tree is full, and the number of nodes of the left subtree is 2h1-1. Then recursively find the right subtree.
• If h 1 and H 2 are not equal, the number of nodes in the right subtree is 2 h2-1. Then recursively find the number of nodes in the left subtree.
  
  

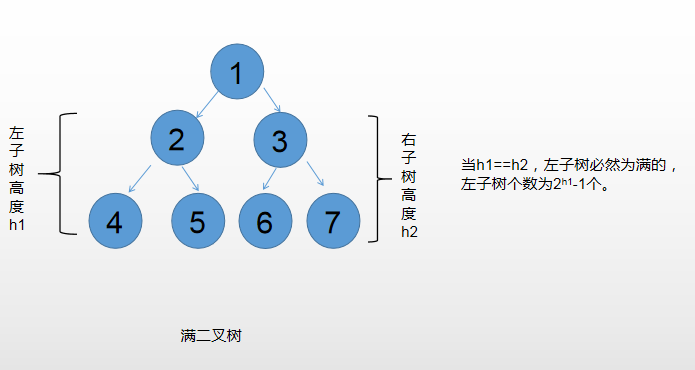
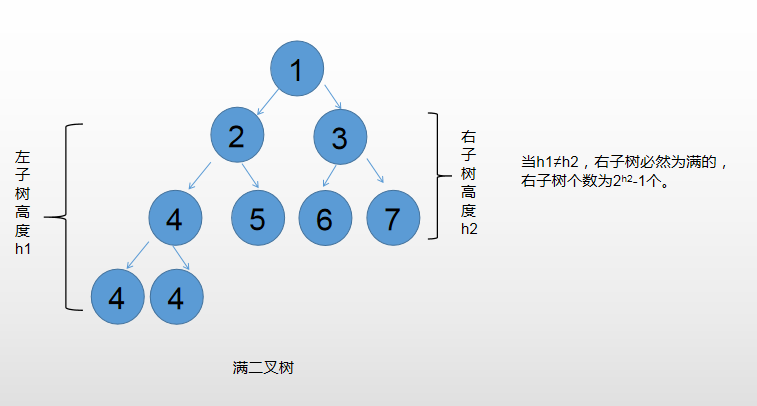
Code:

public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static int nodeNum(Node head) {
		if (head == null) {
			return 0;
		}
		return bs(head, 1, mostLeftLevel(head, 1));
	}

	public static int bs(Node node, int l, int h) {//l is the layer, h is the depth of the whole tree
		if (l == h) {//If you come to the last floor
			return 1;//Leaf node
		}
		if (mostLeftLevel(node.right, l + 1) == h) {//The leftmost depth of the right subtree does not reach the depth of the whole tree
			return (1 << (h - l)) + bs(node.right, l + 1, h);//(the number of nodes in the left tree plus the current node) + recursively find the number of nodes in the right subtree
		} else {
			return (1 << (h - l - 1)) + bs(node.left, l + 1, h);//(the number of right subtree nodes plus the number of current nodes) + recursively find the number of left subtree nodes
		}
	}

	public static int mostLeftLevel(Node node, int level) {//Find the depth of the tree
		while (node != null) {
			level++;
			node = node.left;
		}
		return level - 1;
	}