Computer graphics -- basic graphics algorithms

Representation of points in raster graphics

The screen coordinate system is in the upper left corner

Address = (xmax xmin) [number of pixels per line] * (Y-Ymin) [number of lines] + (X-Xmin) [position in line] + base address

Linear scan conversion algorithm

Assumptions: uniform grid between pixels, integer coordinate system, linear segment slope 0 < K < 1; for k > 1, x and y are interchanged;

• Numerical differentiation algorithm (DDA)

y = m x + b y=mx+b y=mx+b

m = ( y 2 − y 1 ) / ( x 2 − x 1 ) , b = ( x 2 y 1 − x 1 y 2 ) / ( x 2 − x 1 ) m=(y2-y1)/(x2-x1),b=(x2y1-x1y2)/(x2-x1) m=(y2−y1)/(x2−x1),b=(x2y1−x1y2)/(x2−x1)

Numerical differentiation:
m = △ y / △ x = ( y i + 1 − y i ) / ( x i + 1 − x i ) m=△y/△x=(yi+1-yi)/(xi+1-xi) m=△y/△x=(yi+1−yi)/(xi+1−xi)

void DDALine(int x1,int y1,int x2,int y2)
{
    double dx,dy,e,x,y;
    dx=x2-x1;
    dy=y2-y1;
    e=(fabs(dx)>fabs(dy))?fabs(dx):fabs(dy);
    dx/=e;
    dy/=e;
    x=x1;
    y=y1;
    for(int i=1;i<=e;i++)
    {
        SetPixel((int)(x+0.5),(int)(y+0.5));
        x+=dx;
        y+=dy;
    }
}

• Midpoint drawing method

F ( x , y ) = a x + b y + c = 0 F(x,y)=ax+by+c=0 F(x,y)=ax+by+c=0

a = y 0 − y 1 ; b = x 1 − x 0 ; c = x 0 y 1 − x 1 y 0 a=y0-y1;b=x1-x0;c=x0y1-x1y0 a=y0−y1;b=x1−x0;c=x0y1−x1y0

d 0 : F ( x 0 + 1 , y 0 + 0.5 ) , d 0 = a + 0.5 b ; d ≥ 0 : F ( x i + 2 , y + 0.5 ) , 2 d 0 + 2 a ; d < 0 : F ( x i + 2 , y + 1.5 ) , 2 d 0 + 2 a + 2 b d0:F(x0+1,y0+0.5),d0=a+0.5b;d≥0:F(xi+2,y+0.5),2d0+2a;d<0:F(xi+2,y+1.5),2d0+2a+2b d0:F(x0+1,y0+0.5),d0=a+0.5b;d≥0:F(xi+2,y+0.5),2d0+2a;d<0:F(xi+2,y+1.5),2d0+2a+2b

void Midpoint Line(int X0,int y0,int x1,int y1,int color)
{
    int a,b,d1,d2,d,x,y;
    a=y0-y1;b=x1-x0;d=2*a+b;
    d1=2*a;d2=2*(a+b);
    x=x0,y=y0;
    drawpixel(x,y,color);
    while(x<x1)
    {
        if(d<0){x++,y++,d+=d2;}
        else{x++;d+d1;}
        drawpixel(x,y,color);
    }
}

• Bresenham line drawing algorithm

The algorithm and reasoning are similar to the midline drawing method

void BresenhamLine(int x1,int y1,int x2,int y2)
{
    int x,y,dx,dy,p;
    x=x1;
    y=y1;
    dx=x2-x1;
    dy=y2-y1;
    p=2*dy-dx;
    for(;x<=x2;x++)
    {
        SetPixel(x,y);
        if(p>=0)
        {
            y++;
            p+=2*(dx-dy);
        }
        else
        {
            p+=2*dy;
        }
    }
}

Scan conversion algorithm of circle

• Positive and negative method

Basic principle: assuming that Pi-1 has been selected as the i-1 pixel, if Pi-1 is inside the circle, take a step outside the circle; if it is outside the circle, take a step inside the circle. In short, try to be close to the contour of the circle.

Basic algorithm: representation of circle: if the center of the circle is (0,0) and the radius is R, the equation of the circle is:
F ( x , y ) = x 2 + y 2 − R 2 = 0 F(x,y)=x^2+y^2-R^2=0 F(x,y)=x2+y2−R2=0
When the point (x,y) is in the circle, f (x,y) < 0
When the point (x,y) is outside the circle, f (x,y) > 0

Steps: 1. x0=0, y0=R; 2. The principle of finding Pi+1 after obtaining Pi (xi, yi):

① When Pi is in the circle (F(xi,yi) ≤ 0), take a step to the right to get Pi+1, which is to go to the outside of the circle. Take xi+1= xi+1, yi+1= yi
② When Pi is outside the circle (f (Xi, Yi) > 0), go down one step to get Pi+1, which is to go to the inner direction of the circle, and take xi+1= xi, yi+1= yi-1

The recurrence formula is:

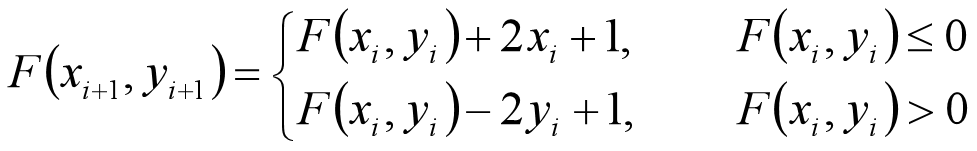
void Posandneg methods(int R,int p1,int p2,int color)
{
    int x,y,x0,y0;
    x0=p1;y0=p2+R;
    x=x0;y=y0;
    int F0=(x0-p1)*(x0-p1)+(y0-p2)*(y0-p2)-R*R;
    int F1=F0;
    int F2;
    while(x<=y)
    {
        if(F1<=0)
        {
            F2=F1+2x+1;
            x=x+1;   
        }
        else
        {
            F2=F1-2y+1;
            y=y+1;
        }
        drawpixel(x,y,color);
    }
}

• Bresenham circle drawing algorithm

Basic principle: assuming that the center of the circle (0,0) is the origin and considering the drawing method of AB arc, when displaying a whole circle, as long as any point (x,y) of AB is displayed, the other seven symmetrical points (y, x), (y, - x), (x, - y), (x, - y), (y, - x), (y, - x), (y, x), (x, x), (x, x,y) on the circumference are displayed at the same time.

Basic algorithm:

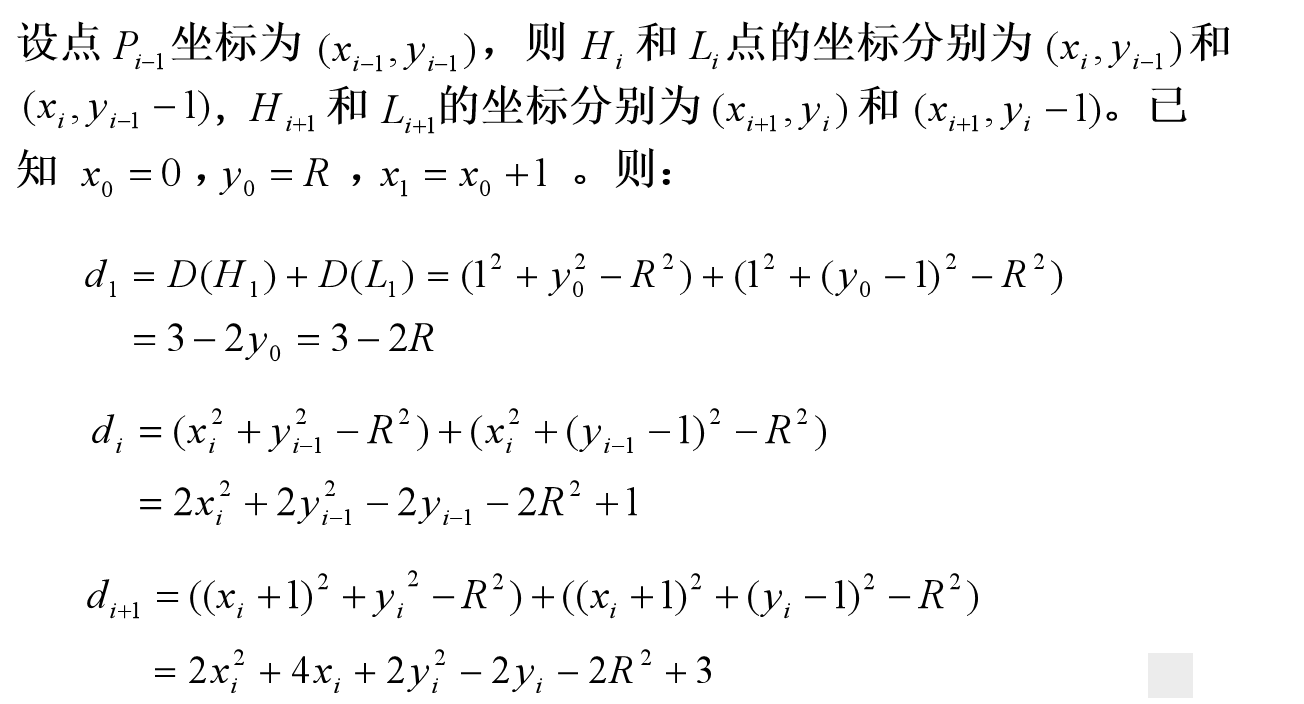
void BresenhamCircle(int R)
{
    int x,y,p;
    int x=0;
    int y=R;
    p=3-2*R;
    for(;x<=y;x++)
    {
        SetPixel(x,y);
        if(p>=0)
        {
            p+=4*(x-y)+10;
            y--;
        }
        else
        {
            p+=4*x+6;
        }
    }
}

• Polygon approach method of circle

Basic idea: divide the whole arc into short lines, and use the polylines formed by these short lines to approach the arc. In order to obtain these short lines, only a series of vertices on the given arc trajectory need to be calculated in a certain way. The generation algorithm of lines can be used for the drawing of short lines. If the arc is divided closely enough, the short lines will be short enough, and the formed polylines will be able to be drawn The arc is close to any degree, so the display polyline can be used to replace the display arc within the allowable error range.

Basic algorithm:

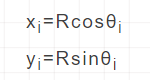
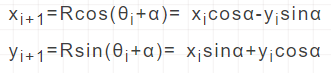
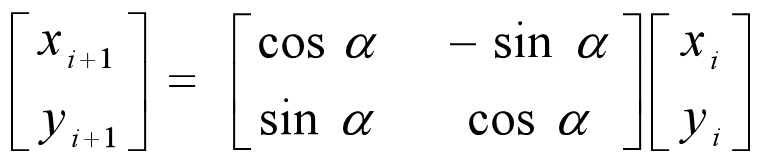
void approachPolygon (int R)
{
    int x0,y0,x1,y1,n;
    double θi,α;
    θi=0;
    x0=Rcos(θi)*180/3.14;
    y0=Rsin(θi)*180/3.14;
    g.drawpoint(x0,y0);
    for(α=0.1;α<=1;α=α+0.1)
    {
        n++;
        x1=x0cos(α)*180/3.14-y0sin(α)*180/3.14;
        y1=x0cos(α)*180/3.14-y0sin(α)*180/3.14;
        g.drawpoint(x1,y1);
        if(α>=1) α=α-1;
        if(n>=3600) break;
    }
}

Elliptic circle scanning conversion algorithm ※

• Midpoint ellipse scan conversion algorithm

void MidpointEllipse(int a,int b)
{
    int x,y;
    double d1,d2;
    x=0;y=b;
    d1=b*b+a*a*(-b+0.25);
    SetPixel(x,y);
    while(b*b*(x+1)<a*a*(y-0.5))
    {
        if(d1<0)
        {
            d1+=b*b*(2*x+3);
            x++;
        }
        else
        {
            d1+=(b*b*(2*x+3)+a*a*(-2*y+2));
            x++;
            y--;
        }
        SetPixel(x,y);
    }
    d2=b*b*(x+0.5)*(x+0.5)+a*a*(-2*y+3);
    while(y>0)
    {
        if(d2>0)
        {
            d2+=a*a*(-2*y+3);
            y--;
        }
        else
        {
            d2+=b*b*(2*x+2)+a*a*(-2*y+3);
            x++;
            y--;
        }
        SetPixel(x,y);
    }
}