1 data structure concept

1.1 origin of data structure

Computer from solving numerical problems to solving problems in life
Problems in real life involve complex connections between different individuals
It is necessary to describe the connections between individuals in life in computer programs
Data structure mainly studies the operation objects and the relationship between them in non numerical program problems, not complex algorithms

1.2 basic concepts in data structure

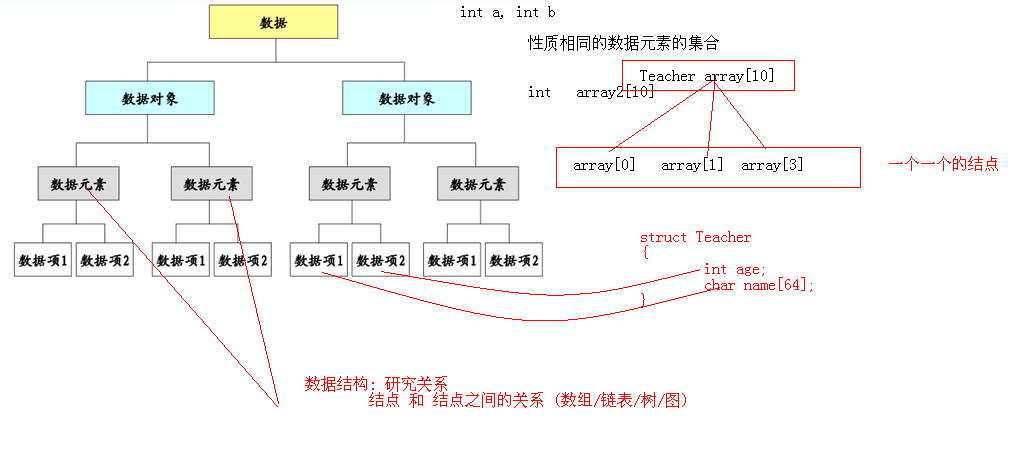
Data - the operation object of the program, which is used to describe objective things (int a,int b)
Characteristics of data:
  can be input to the computer
  can be processed by computer
Data is an abstract concept. After classifying it, we get the types in programming language. Such as int, float, char, etc
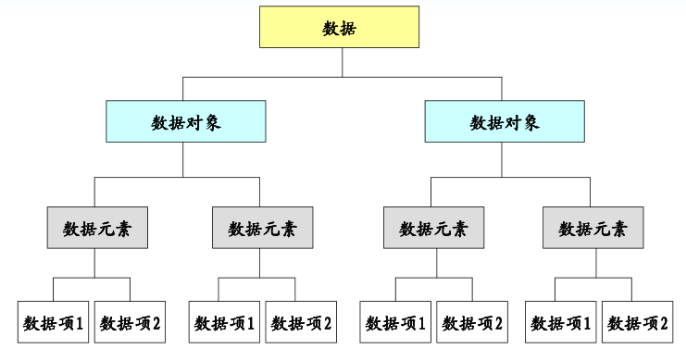
Data element: the basic unit of data
Data item: a data element consists of several data items
Data object: a collection of data elements of the same nature (such as arrays and linked lists)

//Declare a struct type
struct _MyTeacher   //A data type
{
	char	name[32];
	char	tile[32];
	int		age;
	char	addr[128];
};

int main21()
{
	struct _MyTeacher  t1; //data elements
	struct _MyTeacher tArray[30]; //data object
	memset(&t1, 0, sizeof(t1));

	strcpy(t1.name, "name"); //data item
	strcpy(t1.addr, "addr"); //data item
	strcpy(t1.tile, "addr"); //data item
	t1.age = 1;
}

Data elements are not independent and have specific relationships

Data structure refers to the relationship between the data elements in the data object, such as the fixed linear relationship between the elements in the array

Before writing a "good" program, we must analyze the characteristics of each object in the problem to be handled and the relationship between objects

Basic summary:

1.3 logical relationship of data

Refers to the logical relationship between data elements. That is to describe data from relational logic. It has nothing to do with data storage and is independent of computer.


The logical structure can be divided into four categories:

1.4 physical structure of data

1.5 data operation

2 algorithm

2.1 algorithm concept

An algorithm is a description of a specific problem solving step
It is expressed as a finite sequence in a computer
Algorithm is an independent method and idea to solve problems
For algorithm 1, language is not important, what is important is thought

2.2 difference between algorithm and data structure

The data structure only statically describes the relationship between data elements
Efficient programs need to design and select algorithms based on data structures

Program = data structure + algorithm

Summary:
  the algorithm is designed to solve practical problems
  data structure is the problem carrier that the algorithm needs to deal with
  data structures and algorithms complement each other

2.3 algorithm characteristics

Input: the algorithm has 0 or more inputs Output: the algorithm has at least one or more outputs Finiteness: the algorithm will end automatically after limited steps without infinite loop Certainty: every step in the algorithm has a clear meaning, and there will be no ambiguity Feasibility: every step of the algorithm is feasible

2.4 measurement of algorithm efficiency

2.4.1 post statistical method

Post statistical method: compare the processing time of different algorithms for the same set of input data

Defects:   in order to obtain the running time of different algorithms, corresponding programs must be written   runtime is heavily dependent on hardware and runtime environmental factors   the data selection of the algorithm is quite difficult

In a word, although the post statistical method is intuitive, it is difficult to implement and has many defects

Measurement of algorithm efficiency
  prior analysis and estimation: estimate the algorithm efficiency according to the statistical method
Main factors affecting algorithm efficiency:
  strategies and methods adopted by the algorithm
  input scale of the problem
  code generated by compiler
  computer execution speed

//The algorithm is finally compiled into specific computer instructions
//Each instruction runs at a fixed speed on a specific computer
//Through the specific steps of n, the complexity of the algorithm can be deduced
long sum1(int n)
{
    long ret = 0;                         
    int* array = (int*)malloc(n * sizeof(int)); 
    int i = 0;  
    
    for(i=0; i<n; i++)   
    {
        array[i] = i + 1;
    }
    
    for(i=0; i<n; i++) 
    {
        ret += array[i];
    }
    
    free(array); 
    
    return ret; 
}

long sum2(int n)
{
    long ret = 0;
    int i = 0;
    
    for(i=1; i<=n; i++)
    {
        ret += i;
    }
    
    return ret;
}

long sum3(int n)
{
    long ret = 0;
    
    if( n > 0 )
    {
        ret = (1 + n) * n / 2; 
    }
    
    return ret;
}

int main()
{
    printf("%d\n", sum1(100));
    printf("%d\n", sum2(100));
    printf("%d\n", sum3(100));
    
    return 0;
}

int func(int a[], int len)
{
    int i = 0;
    int j = 0;
    int s = 0;
    
    for(i=0; i<len; i++) n
    {
        for(j=0; j<len; j++) n
        {
            s += i*j;  //n*n
        }
    }
    return s; 
}
//n*n

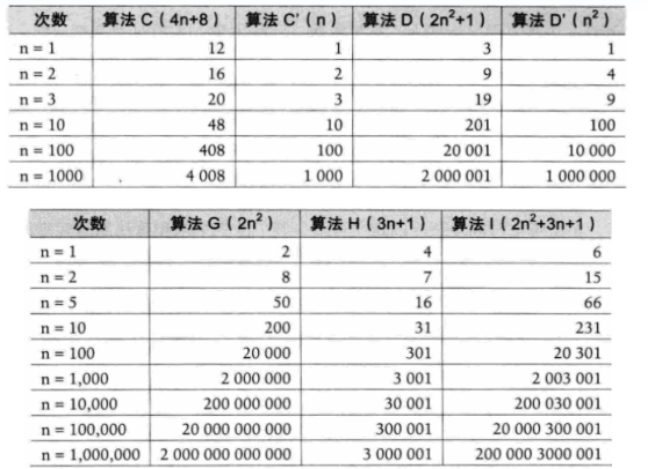
Note 1: when judging the efficiency of an algorithm, we often only need to pay attention to the highest order item of the number of operations, and other secondary items and constant items can be ignored.
Note 2: without special instructions, the time complexity of the algorithm we analyze refers to the worst time complexity.

2.4.2 large O representation

Algorithm efficiency depends heavily on the number of operation s
When judging, first pay attention to the highest order item of the operation quantity
The estimation of operation quantity can be used as the estimation of time complexity
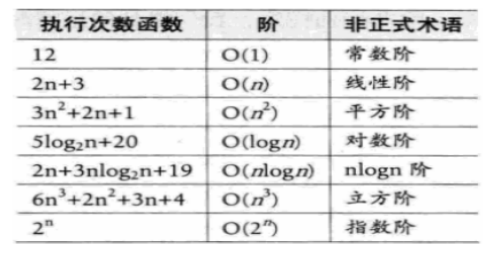
O(5) = O(1)
O(2n + 1) = O(2n) = O(n)
O(n2+ n + 1) = O(n2)
O(3n3+1) = O(3n3) = O(n3)
Common time complexity:

Relationship:

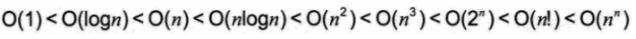
2.4.3 spatial complexity of algorithm

The spatial complexity of the algorithm is calculated by calculating the storage space of the algorithm
S(n) = O(f(n))
Where n is the problem scale, and f(n)) is a function of the storage space occupied when the problem scale is n
The large O representation is also suitable for the spatial complexity of the algorithm
When the space required for the execution of the algorithm is constant, the space complexity is O(1)

Space and time strategy   in most cases, the time spent in the execution of the algorithm is more concerned   if necessary, the time complexity can be reduced by increasing the space complexity   similarly, the space complexity can also be reduced by increasing the time complexity

//Time for space 
/*
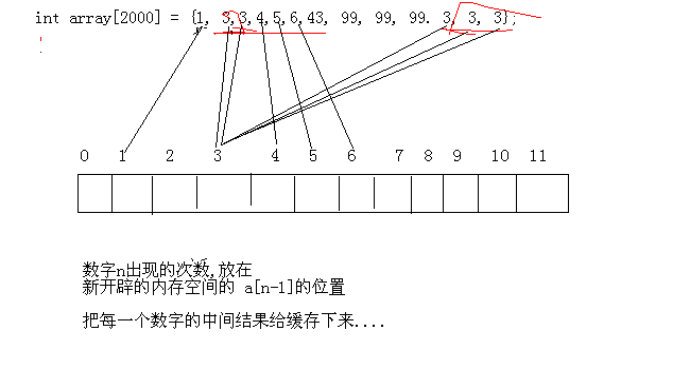
    Question: 
    In an array of natural numbers 1-1000, each number may appear zero or more times.
    Design an algorithm to find the number that appears the most.
*/
Method 1:
   Sort and find the number that appears the most

Method 2:
void search(int a[], int len)
{
    int sp[1000] = {0};
    int i = 0;
    int max = 0;
    
    for(i=0; i<len; i++)
    {
        int index = a[i] - 1;
        
        sp[index]++;
    }
    
    for(i=0; i<1000; i++)
    {
        if( max < sp[i] )
        {
            max = sp[i];
        }
    }
    
    for(i=0; i<1000; i++)
    {
        if( max == sp[i] )
        {
            printf("%d\n", i+1);
        }
    }
}

int main()
{
    int array[] = {1, 1, 3, 4, 5, 6, 6, 6, 2, 3};
    
    search(array, sizeof(array)/sizeof(*array));
    
    return 0;
}

Cache the intermediate result of the number of occurrences of each number; Maximize the cached results.