recursion

The programming skill of program calling itself is called recursion

public static void show(){
       show();
}

It usually transforms a large and complex problem into a smaller problem which is similar to the original problem. The recursive strategy only needs a small number of programs to describe the repeated calculation needed in the process of solving the problem, which greatly reduces the code amount of the program.
Generally speaking, recursion needs boundary conditions, recursion forward segment and recursion return segment. When the boundary conditions are not satisfied, recursion advances; when the boundary conditions are satisfied, recursion returns.
Recursive forward segment

boundary condition

Recursive return segment

Divide and conquer algorithm

Divide and conquer algorithm is to divide the original problem into n sub problems with small scale and similar structure to the original problem, solve these sub problems recursively, and then combine the results to get the solution of the original problem.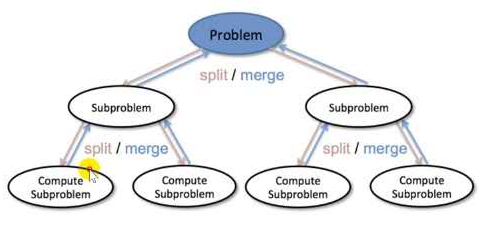

In the recursive implementation of divide and conquer algorithm, each layer of recursion involves three operations as follows:

• Decomposition: decompose the original problem into a series of sub problems.
• Solution: solve each subproblem recursively. If the subproblem is small enough, solve it directly.
• Merge: merge the results of sub problems into the original problems.

The problems that divide and conquer algorithm can solve generally need to meet the following conditions:

• The original problem has the same pattern as the small problem
• The subproblem decomposed from the original problem can be solved independently, and there is no correlation between subproblems
• There are decomposition termination conditions, that is, when the problem is small enough, it can be solved directly
• The subproblem can be merged into the original problem, and the complexity of the merging operation cannot be too high, otherwise it will not reduce the overall complexity of the algorithm.

In addition:

• Any problem that can be solved by mathematical induction can use the idea of divide and conquer
• The idea of divide and rule does not necessarily use recursive structure

Example: sum of the first n items

public class Recursion {
    public static void main(String[] args) {
        //Recursive accumulation O(n)
        test01();
        //Iterative accumulation O(n)
        test02();
    }

    private static void test02() {
        int sum=0;
        int n=100;
        for (int i=0;i<=n;i++){
            sum+=i;
        }
        System.out.println(sum);
    }

    private static void test01() {
        int n=100;
        int sum=sum(n);
        System.out.println(sum);
    }

    private static int sum(int n) {
        if(n==1){
            return 1;
        }
        return sum(n-1)+n;
    }
}

results of enforcement

5050
5050

Example: factorial problem of n

public class Recursion02 {
    public static void main(String[] args) {
        //Recursive factorial
        test01();  //O(n)
        //Iterative factorial
        test02();//O(n)
    }

    private static void test02() {
        int n=10;
        int product=1;
        for (int i=1;i<=n;i++){
            product*=i;
        }
        System.out.println(product);
    }

    private static void test01() {
        int n=10;
        int product=factorial(n);
        System.out.println(product);
    }

    private static int factorial(int n) {
        if(n==1){
            return 1;
        }
        return factorial(n-1)*n;
    }
}

results of enforcement

   3628800
   3628800

Example: Fibonacci sequence problem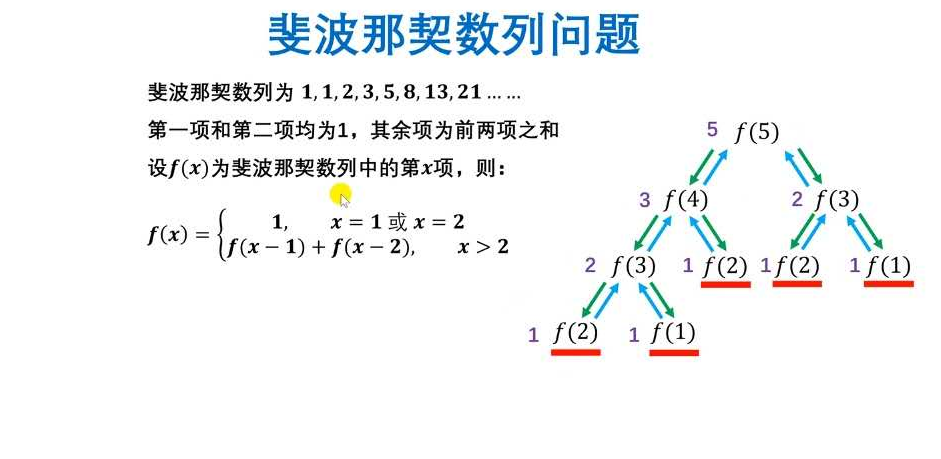

public class Recursion03 {
    public static void main(String[] args) {
        //Recursive Fibonacci series O(2^n)
        test01();
        //Iterative Fibonacci series O(n)
        test02();
    }

    private static void test02() {
        int n=45;
        int num=getFabonacci(n);
        System.out.println(num);
    }

    private static int getFabonacci(int n) {
        if (n==1||n==2){
            return 1;
        }
        int first=1;
        int second=1;
        int current=0;
        for (int i=3;i<=n;i++){
            current=first+second;
            first=second;
            second=current;
        }
        return current;
    }

    private static void test01() {
        int n=5;
        int num=fabonacci(n);
        System.out.println(num);
    }

    private static int fabonacci(int n) {
        if (n==1||n==2){
            return 1;
        }
        return fabonacci(n-1)+fabonacci(n-2);
    }
}

results of enforcement

5
1134903170